Loading...
Back to:
Algebra Multiplication Pyramids (A) WORKSHEET
Suitable for Grades: Algebra I, IM 1
CCSS: HSA.APR.D.6, HSA.SSE.B.3
CCSS Description: Rewrite simple rational expressions in different forms; write a(x)/b(x) in the form q(x) + r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division, or, for the more complicated examples, a computer algebra system.
Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.★ a. Factor a quadratic expression to reveal the zeros of the function it defines. b. Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines. c. Use the properties of exponents to transform expressions for exponential functions. For example the expression 1.15t can be rewritten as (1.151/12)12t ≈ 1.01212t to reveal the approximate equivalent monthly interest rate if the annual rate is 15%
Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.★ a. Factor a quadratic expression to reveal the zeros of the function it defines. b. Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines. c. Use the properties of exponents to transform expressions for exponential functions. For example the expression 1.15t can be rewritten as (1.151/12)12t ≈ 1.01212t to reveal the approximate equivalent monthly interest rate if the annual rate is 15%
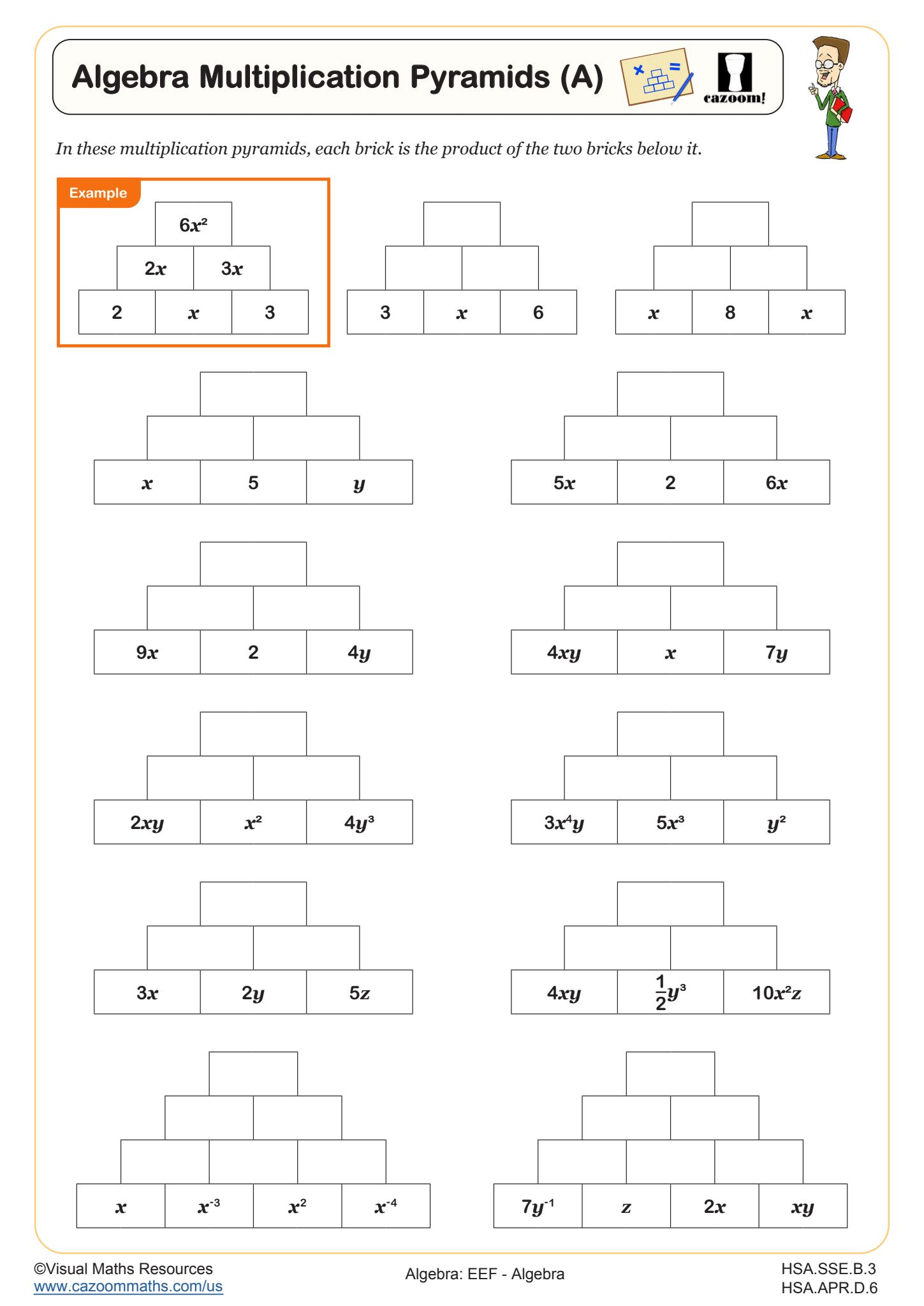
Algebra Multiplication Pyramids (A) WORKSHEET DESCRIPTION
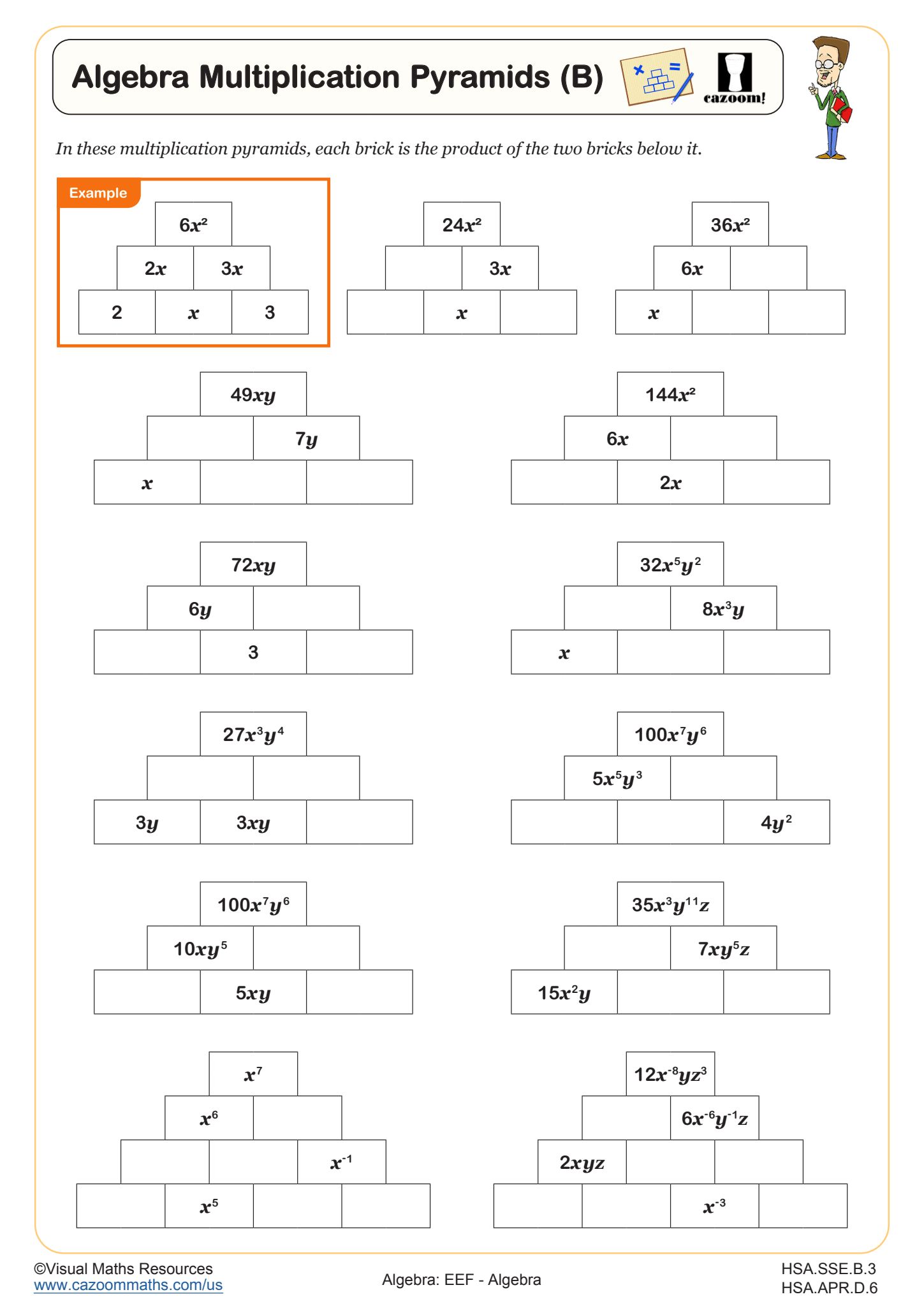
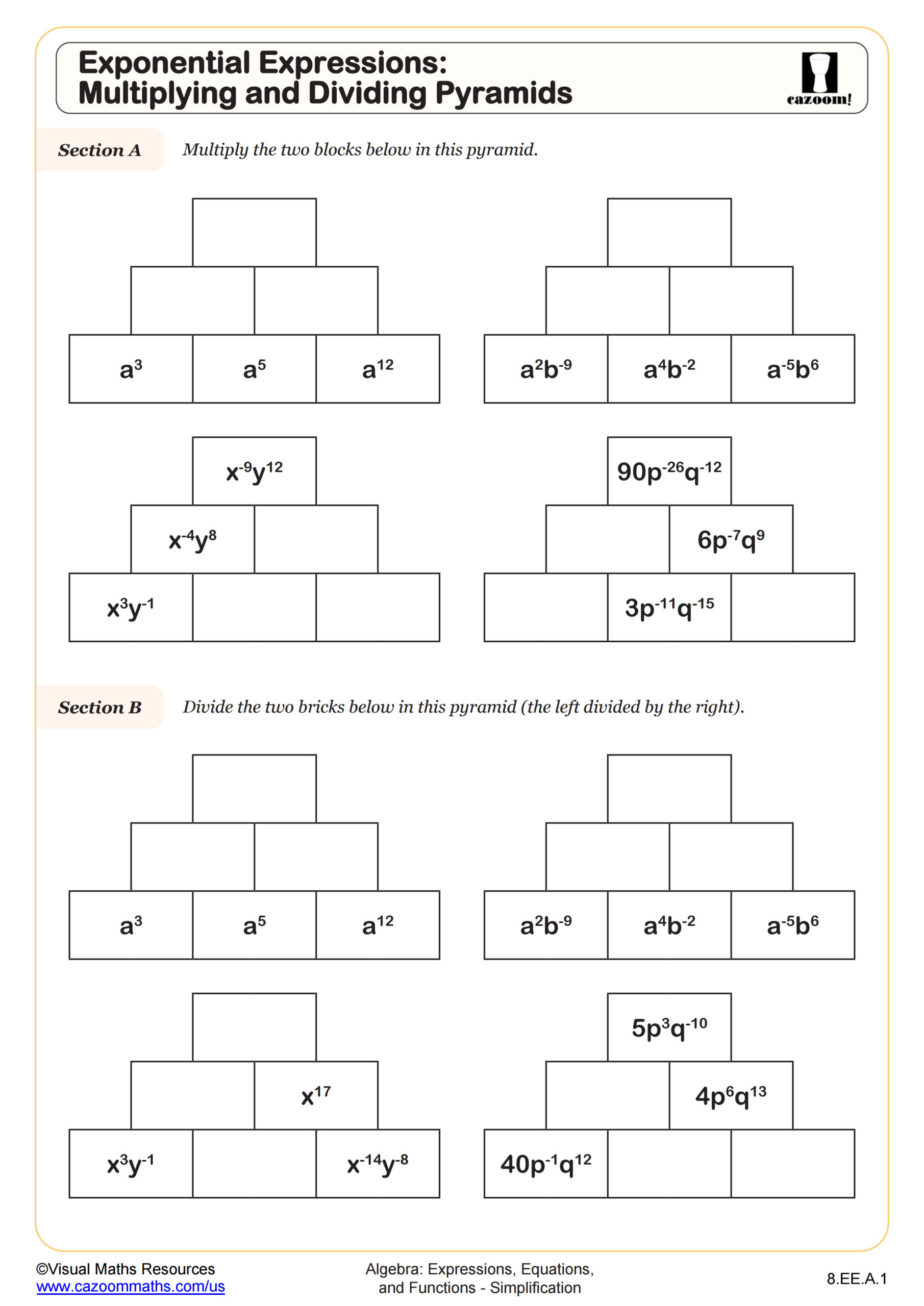
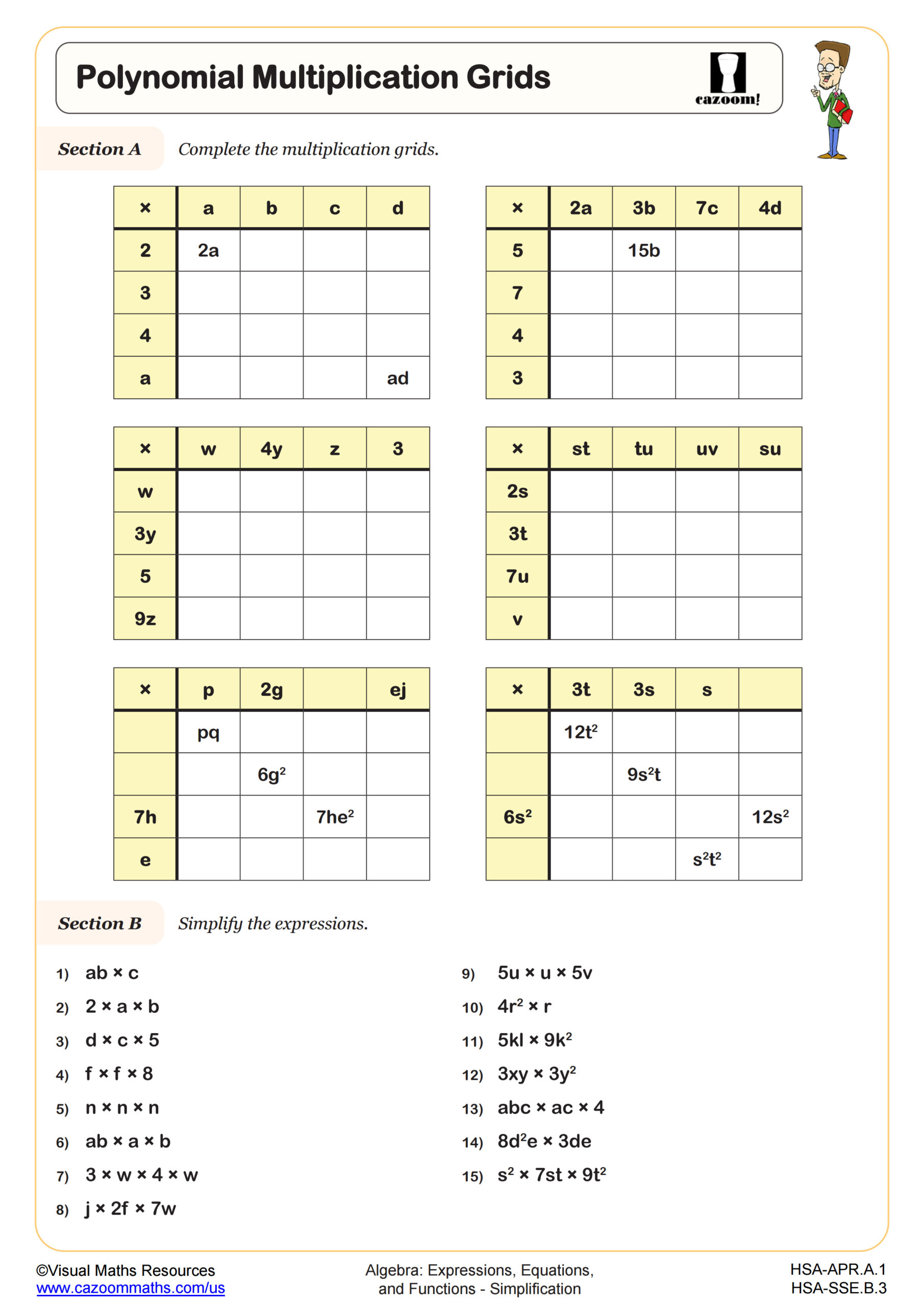
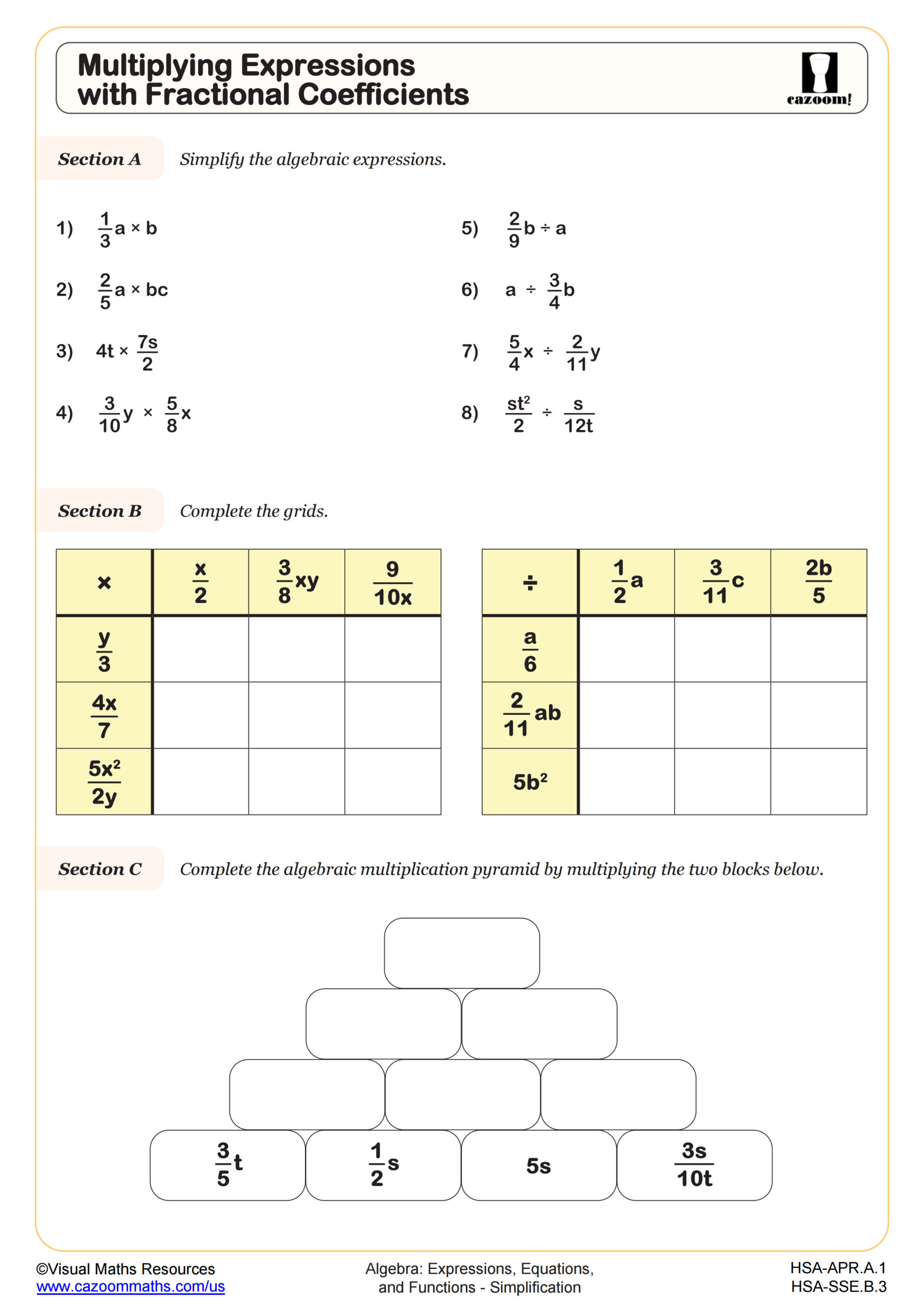
Perfect for learners needing more practice or a variation in their practice, these multiplication pyramids will see learners finding the product of two terms involving up to 3 variables and various coefficients. Students will be working with the multiplication index law throughout.
The pyramids are completed by finding the product of two adjacent bricks, the answer then goes in the brick above. All pyramids are made up of six bricks and can be completed without the division of any terms.
Ready for the next challenge? Try Algebra Multiplication Pyramids (B).
