Back to:
Calculating Bearings - with Angles in Parallel Lines WORKSHEET
Suitable for Grades: 7th Grade, Geometry
CCSS: 7.G.A.1, HSG.CO.D.12
CCSS Description: Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
Calculating Bearings - with Angles in Parallel Lines WORKSHEET DESCRIPTION
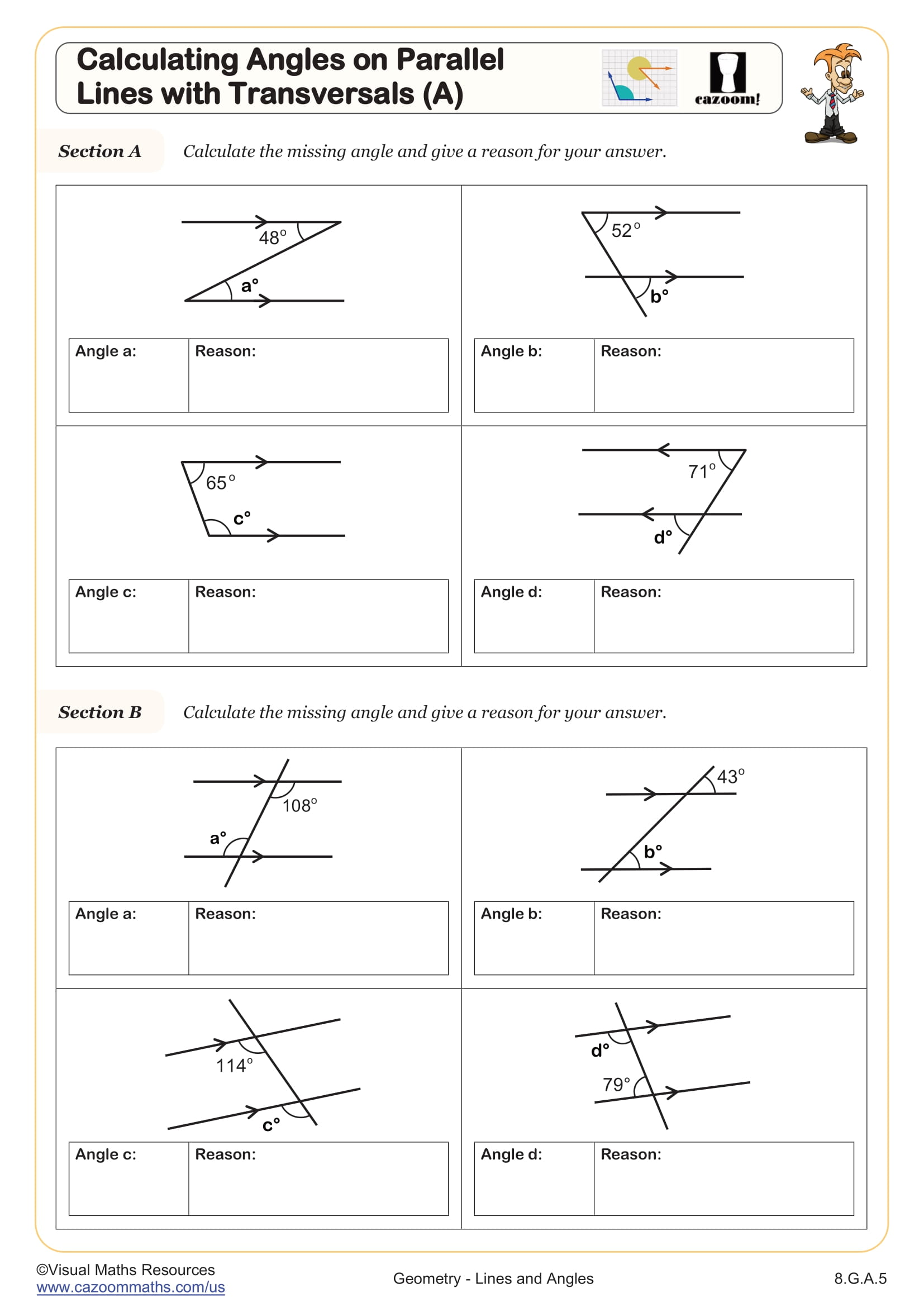
This worksheet will help learners calculate bearings using parallel line angle properties. Each diagram is not drawn to scale so learners will need to apply their knowledge of co-interior, corresponding, and alternate angles to solve bearing problems.
Sections A to C systematically introduce each parallel line rule separately, allowing learners to develop proficiency with co-interior, corresponding, and alternate angles before progressing to more complex problems where they must select the most appropriate method.
Section D asks learners to demonstrate how to find reverse bearings using all three angle rules, reinforcing their understanding of the different methods.
Section E provides mixed practice questions where students can choose their preferred method to calculate bearings, plus specific problems involving return bearings with step-by-step working requirements.
Sections A to C systematically introduce each parallel line rule separately, allowing learners to develop proficiency with co-interior, corresponding, and alternate angles before progressing to more complex problems where they must select the most appropriate method.
Section D asks learners to demonstrate how to find reverse bearings using all three angle rules, reinforcing their understanding of the different methods.
Section E provides mixed practice questions where students can choose their preferred method to calculate bearings, plus specific problems involving return bearings with step-by-step working requirements.
