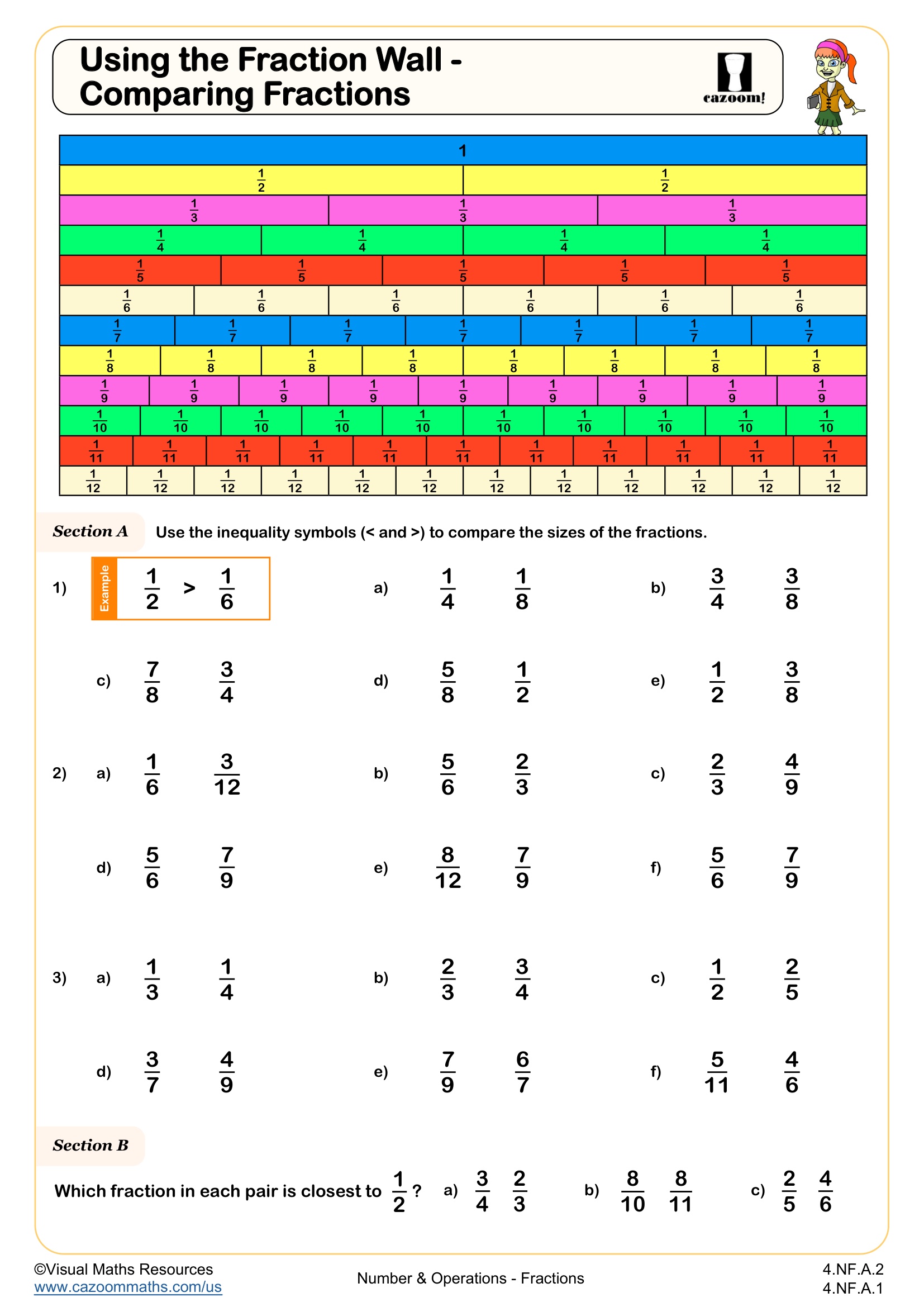
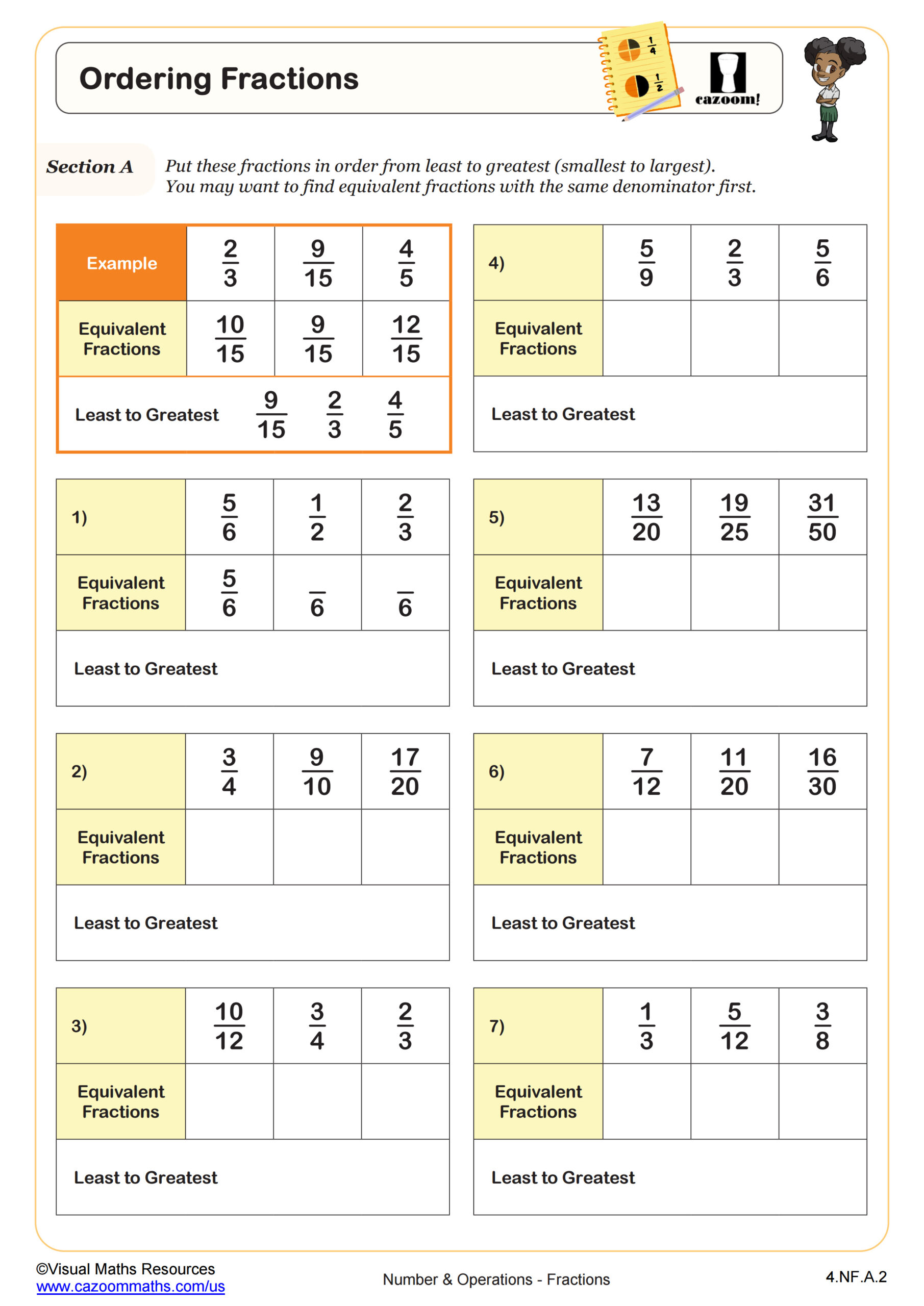
Back to:
Comparing Fractions WORKSHEET
Suitable for Grades: 3rd Grade, 4th Grade
CCSS: 3.NF.A.3, 4.NF.A.2
CCSS Description: Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size. a. Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line. b. Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3). Explain why the fractions are equivalent, e.g., by using a visual fraction model. c. Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram. d. Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
Comparing Fractions WORKSHEET DESCRIPTION
This worksheet develops students’ ability to compare fractions using inequality signs.
In Section A, students compare unit and non-unit fractions with the same numerators and complete a sentence explaining how fraction size is affected by the denominator when the numerators are equal.
Section B focuses on comparing fractions with the same denominators, prompting learners to identify how greater numerators affect the value of a fraction.
Section C deepens understanding by guiding students to create equivalent fractions with common denominators before comparing them. In this section, one denominator is a multiple of the other in each pair.
Section D presents more challenging comparisons, requiring students to convert both fractions to equivalent forms before making comparisons.
This worksheet reinforces essential skills in fraction comparison and supports the development of fluency and reasoning.
In Section A, students compare unit and non-unit fractions with the same numerators and complete a sentence explaining how fraction size is affected by the denominator when the numerators are equal.
Section B focuses on comparing fractions with the same denominators, prompting learners to identify how greater numerators affect the value of a fraction.
Section C deepens understanding by guiding students to create equivalent fractions with common denominators before comparing them. In this section, one denominator is a multiple of the other in each pair.
Section D presents more challenging comparisons, requiring students to convert both fractions to equivalent forms before making comparisons.
This worksheet reinforces essential skills in fraction comparison and supports the development of fluency and reasoning.
