Continuing Sequences from Patterns WORKSHEET
Recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of the integers. For example, the Fibonacci sequence is defined recursively by f(0) = f(1) = 1, f(n+1) = f(n) + f(n–1) for n ≥ 1.
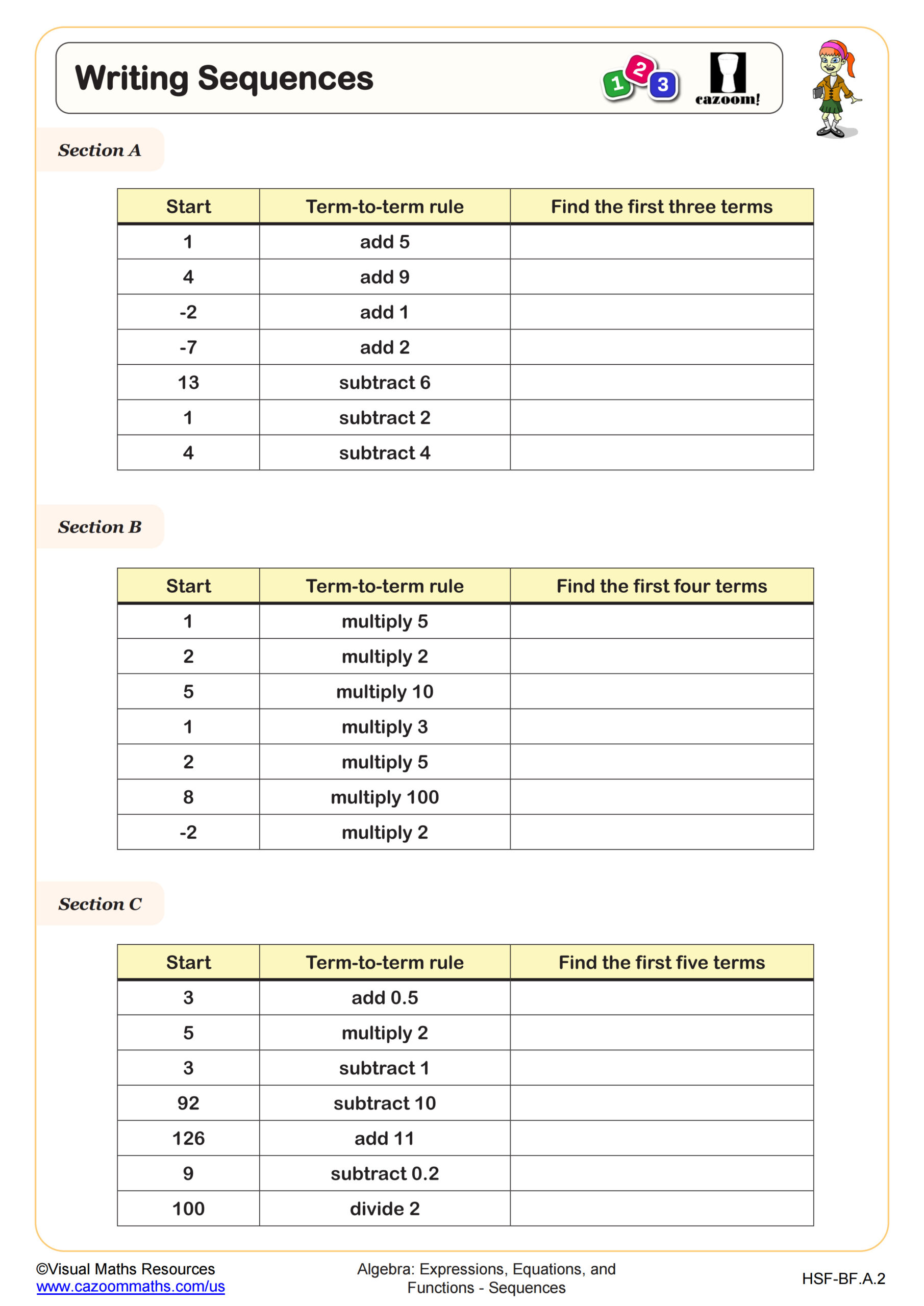
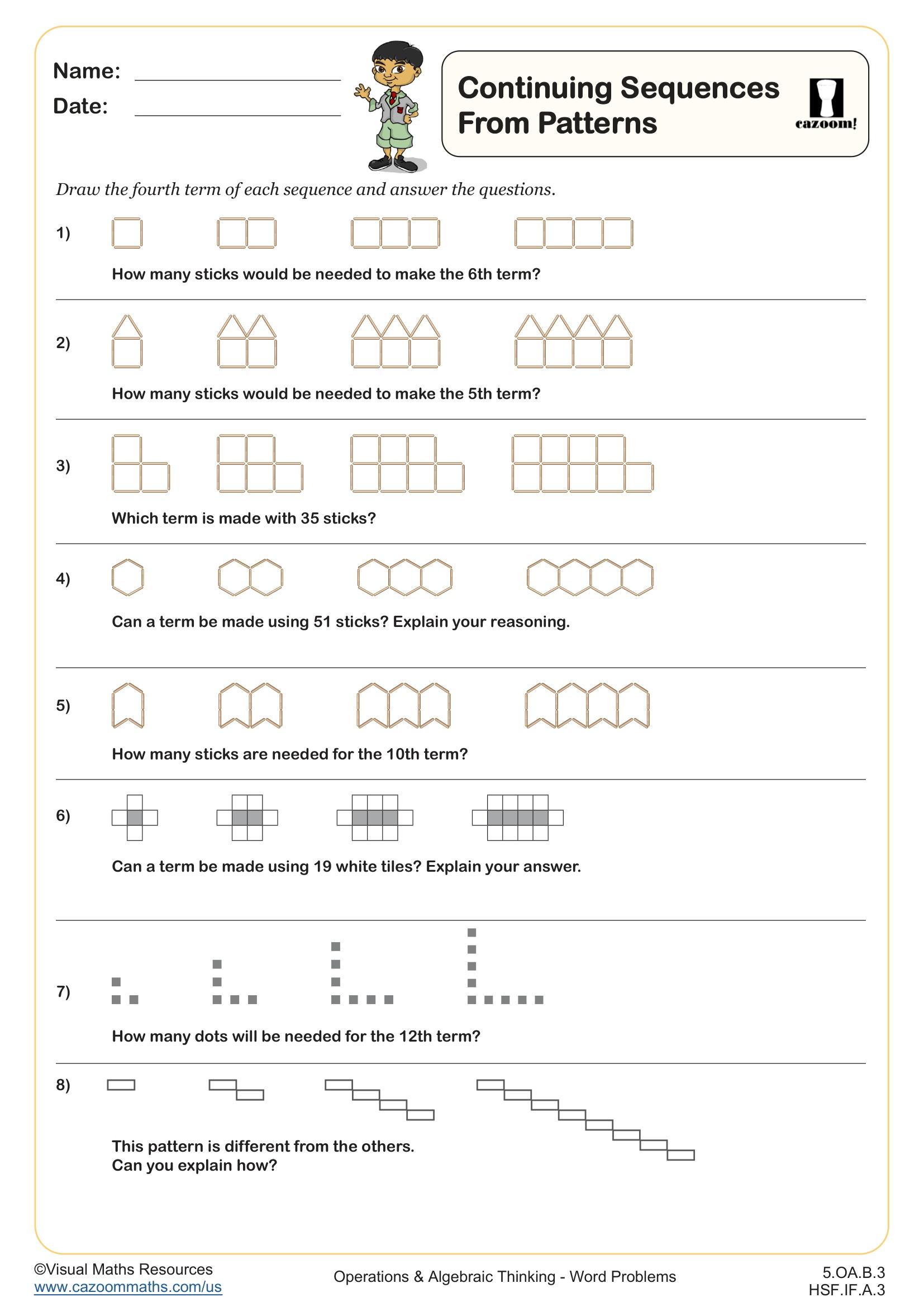
Continuing Sequences from Patterns WORKSHEET DESCRIPTION
This worksheet presents a series of diagrammatic sequences, each with only the first three terms displayed.
Learners will draw the fourth term of each of these sequences as well as answering questions such as “How many sticks will be needed for the 6th term?” and “Can a term be made using 19 white tiles?”.
The first 8 sequences are linear and the last pattern represents a geometric progression.
This time students are asked to consider how this sequence is different from the others.
The patterns are made using sticks, white and grey tiles and dots.
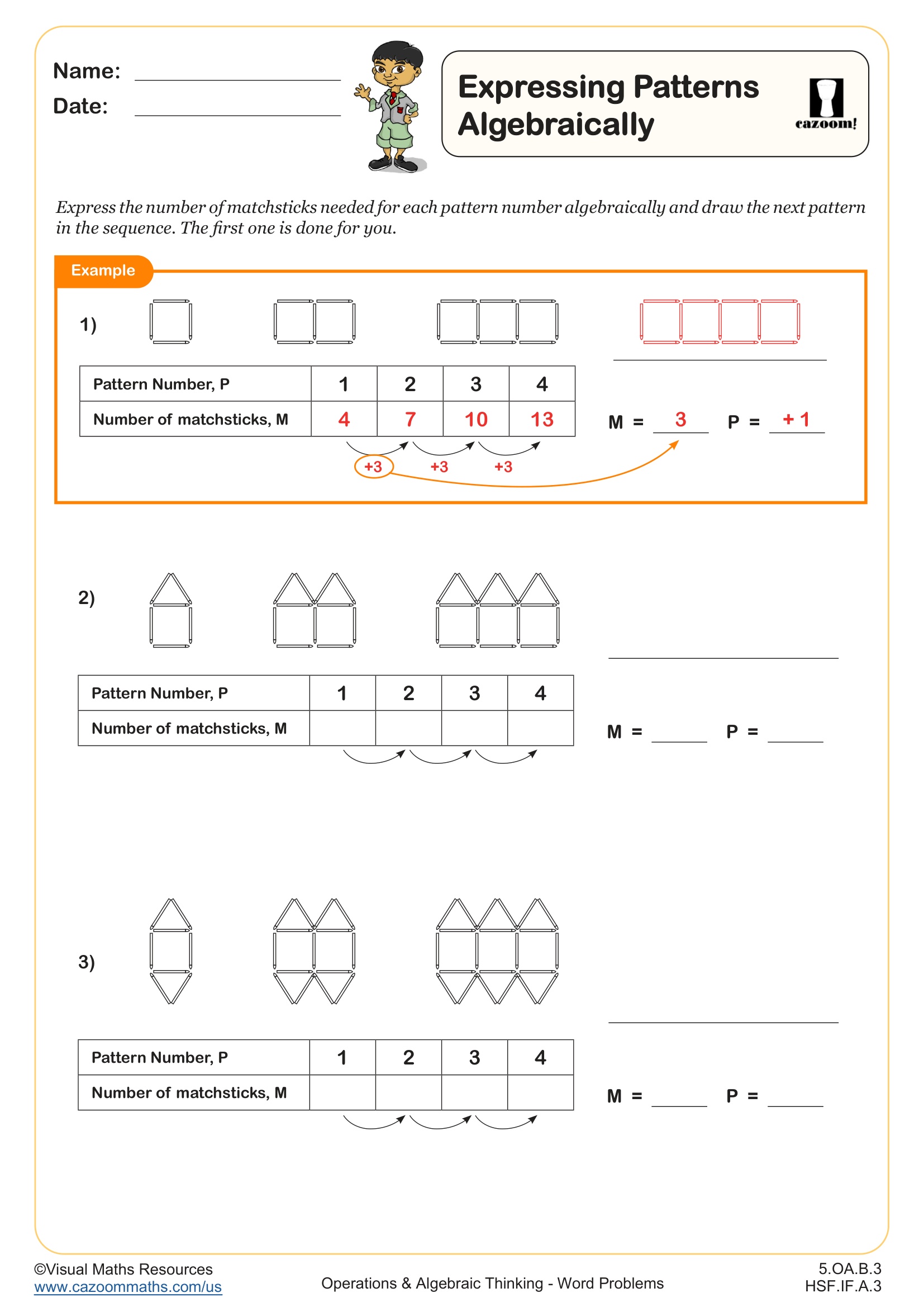
To start linking sequences and algebra see our worksheet “Expressing Patterns Algebraically”.
RELATED TO Continuing Sequences from Patterns WORKSHEET
Frequently Asked Questions
This continuing sequences from patterns worksheet is designed for students in 5th Grade, Algebra I, and IM 1 and aligns with Common Core State Standards.