Crossing Zero (A) WORKSHEET
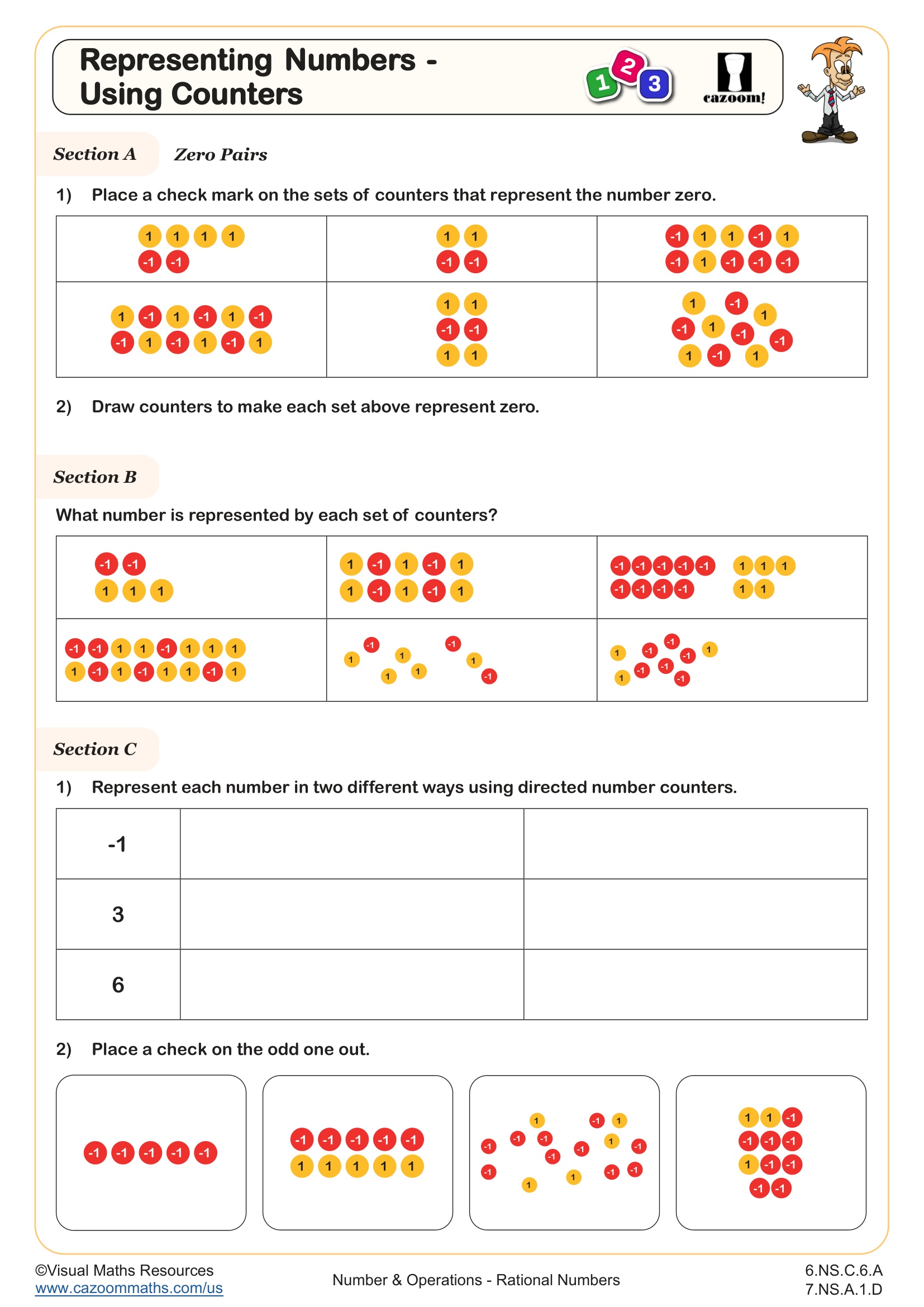
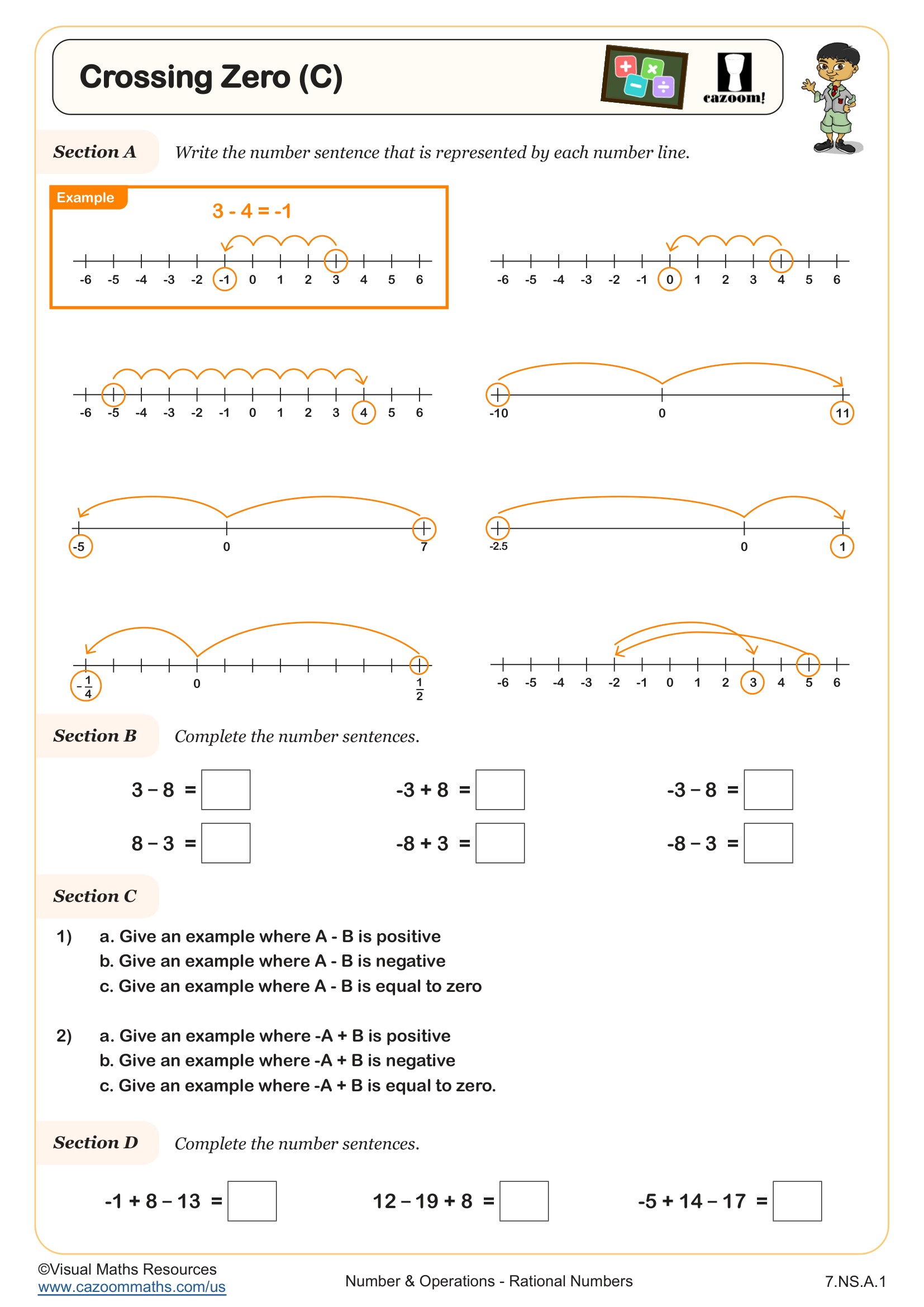
Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram. a. Describe situations in which opposite quantities combine to make 0. For example, a hydrogen atom has 0 charge because its two constituents are oppositely charged. b. Understand p + q as the number located a distance |q| from p, in the positive or negative direction depending on whether q is positive or negative. Show that a number and its opposite have a sum of 0 (are additive inverses). Interpret sums of rational numbers by describing real-world contexts. c. Understand subtraction of rational numbers as adding the additive inverse, p – q = p + (–q). Show that the distance between two rational numbers on the number line is the absolute value of their difference, and apply this principle in real-world contexts. d. Apply properties of operations as strategies to add and subtract rational numbers.
Crossing Zero (A) WORKSHEET DESCRIPTION
This worksheet provides learners with different strategies for calculating across zero. All questions here involve adding a positive number to a negative number and will aid in pupils understanding the symmetry of zero and prepare them for further calculations with positive and negative numbers.
Number lines are used throughout section A to complete addition statements. Three different types of number lines are used and are designed to encourage pupils to think about how to partition numbers when calculating with them. In section B, pupils will use partitioning to complete addition statements.
Students then predict whether addition calculations will cross zero or not in section C.

RELATED TO Crossing Zero (A) WORKSHEET
Frequently Asked Questions
This crossing zero (a) worksheet is designed for students in 6th Grade and 7th Grade and aligns with Common Core State Standards.