Menu

BY TOPICBY CCSS
SCHOOLSSEARCH
LOGINFREE TRIAL
Back to:
Ratio

Drawing Conversion Graphs WORKSHEET

Suitable for Grades: 7th Grade, 8th Grade
CCSS: 7.RP.A.2, 8.SP.A.3
CCSS Description: Recognize and represent proportional relationships between quantities. a. Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin. b. Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships. c. Represent proportional relationships by equations. For example, if total cost t is proportional to the number n of items purchased at a constant price p, the relationship between the total cost and the number of items can be expressed as t = pn. d. Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.

Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept. For example, in a linear model for a biology experiment, interpret a slope of 1.5 cm/hr as meaning that an additional hour of sunlight each day is associated with an additional 1.5 cm in mature plant height.

Drawing Conversion Graphs WORKSHEET DESCRIPTION

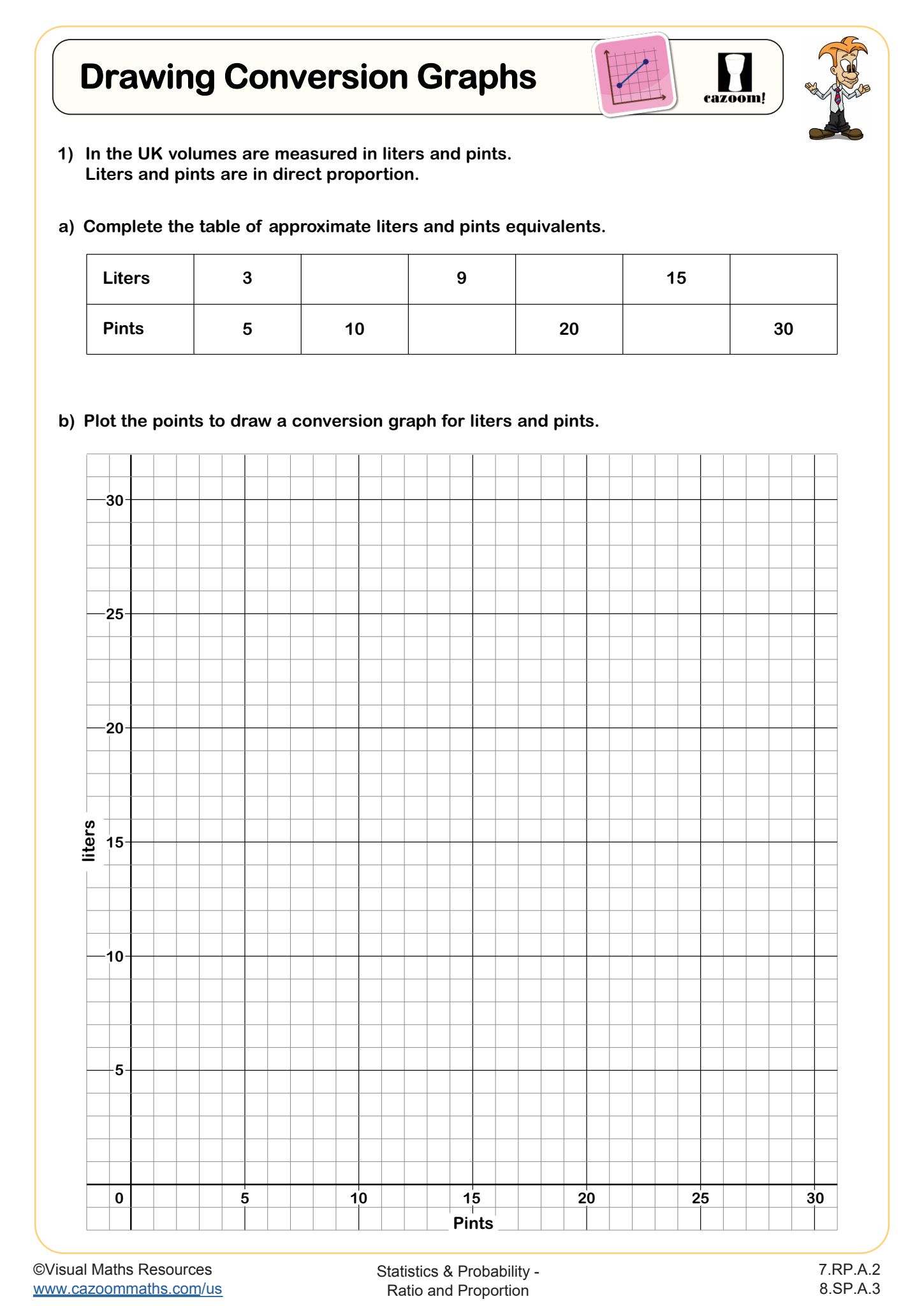
Learners will plot four different conversion graphs across this worksheet.

In question 1, students will plot a graph showing the equivalence between liters and pints. They will complete a table of values before plotting these points on pre-drawn axes.

Next, in question 2, pupils will use the fact that 1 kg ≈ 2.2 pounds to draw a conversion graph.

The graph in question 3 will show the currency conversion between € and $. This time, students are required to label the y-axis appropriately.

Lastly, students will use the approximate formula for converting between degrees Celsius and Fahrenheit to draw a conversion graph in question 4. Again, learners are required to label the y-axis before drawing the graph.

Drawing Conversion Graphs Worksheet suitable for 7th Grade and 8th Grade students

RELATED TO Drawing Conversion Graphs WORKSHEET

Graphing Relationships (A) - Drawing and Interpreting

Grades: 6th Grade, 8th Grade

Preview of Graphing Relationships (A) - Drawing and Interpreting

Using Conversion Graphs

Grades: 7th Grade, 8th Grade

Preview of Using Conversion Graphs

Drawing Distance-Time Graphs

Grades: 8th Grade

Preview of Drawing Distance-Time Graphs

Graphing Relationships (B) - Equations

Grades: 6th Grade, 8th Grade

Preview of Graphing Relationships (B) - Equations

Frequently Asked Questions

This drawing conversion graphs worksheet is designed for students in 7th Grade and 8th Grade and aligns with Common Core State Standards.