Loading...
Finding Fractional Amounts WORKSHEET
Suitable for Grades: 5th Grade, 6th Grade
CCSS: 5.NF.B.4.A, 6.NS.A.1
CCSS Description: Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction. a. Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b. For example, use a visual fraction model to show (2/3) × 4 = 8/3, and create a story context for this equation. Do the same with (2/3) × (4/5) = 8/15. (In general, (a/b) × (c/d) = ac/bd.)
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?
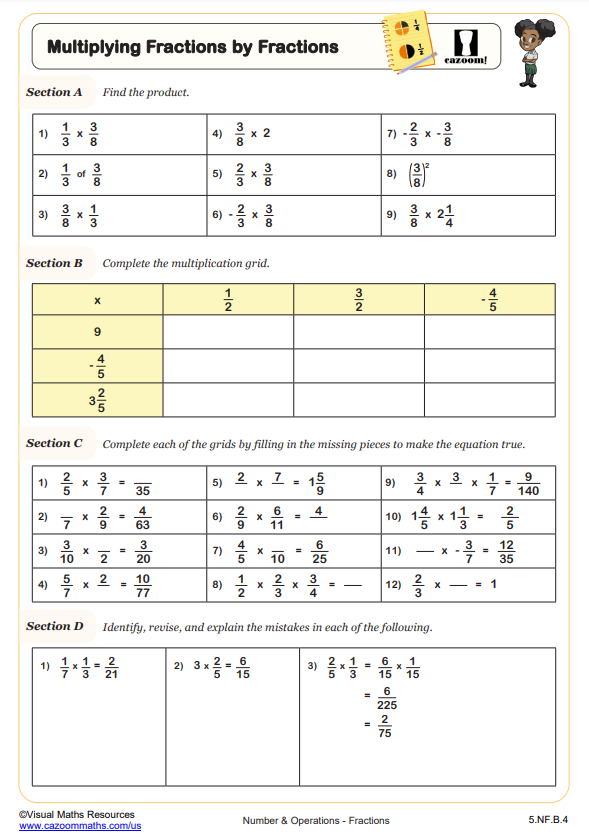
Finding Fractional Amounts WORKSHEET DESCRIPTION
Section A is a set of 12 questions designed so integer answers can be expected and gives students an opportunity to consider what calculation they do to find a unit fraction of an amount.
Students are given a variation in questioning with section B. This section asks learners to complete multiplication grids, multiplying integers by fractions.
Finally, test your learners' knowledge in section C as they answer questions such as ½ of what = 36? and what fraction of 96 is 16?
Now your students should be ready to find non unit fractions of amounts.
