Menu

BY TOPICBY CCSS
SCHOOLSSEARCH
LOGINFREE TRIAL
Back to:
Rational Numbers

Multiplication Using Number Counters WORKSHEET

Suitable for Grades: 7th Grade
CCSS: 7.NS.A.2, 7.NS.A.2.A
CCSS Description: Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers. a. Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (–1)(–1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts. b. Understand that integers can be divided, provided that the divisor is not zero, and every quotient of integers (with non-zero divisor) is a rational number. If p and q are integers, then –(p/q) = (–p)/q = p/(–q). Interpret quotients of rational numbers by describing real-world contexts. c. Apply properties of operations as strategies to multiply and divide rational numbers. d. Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.

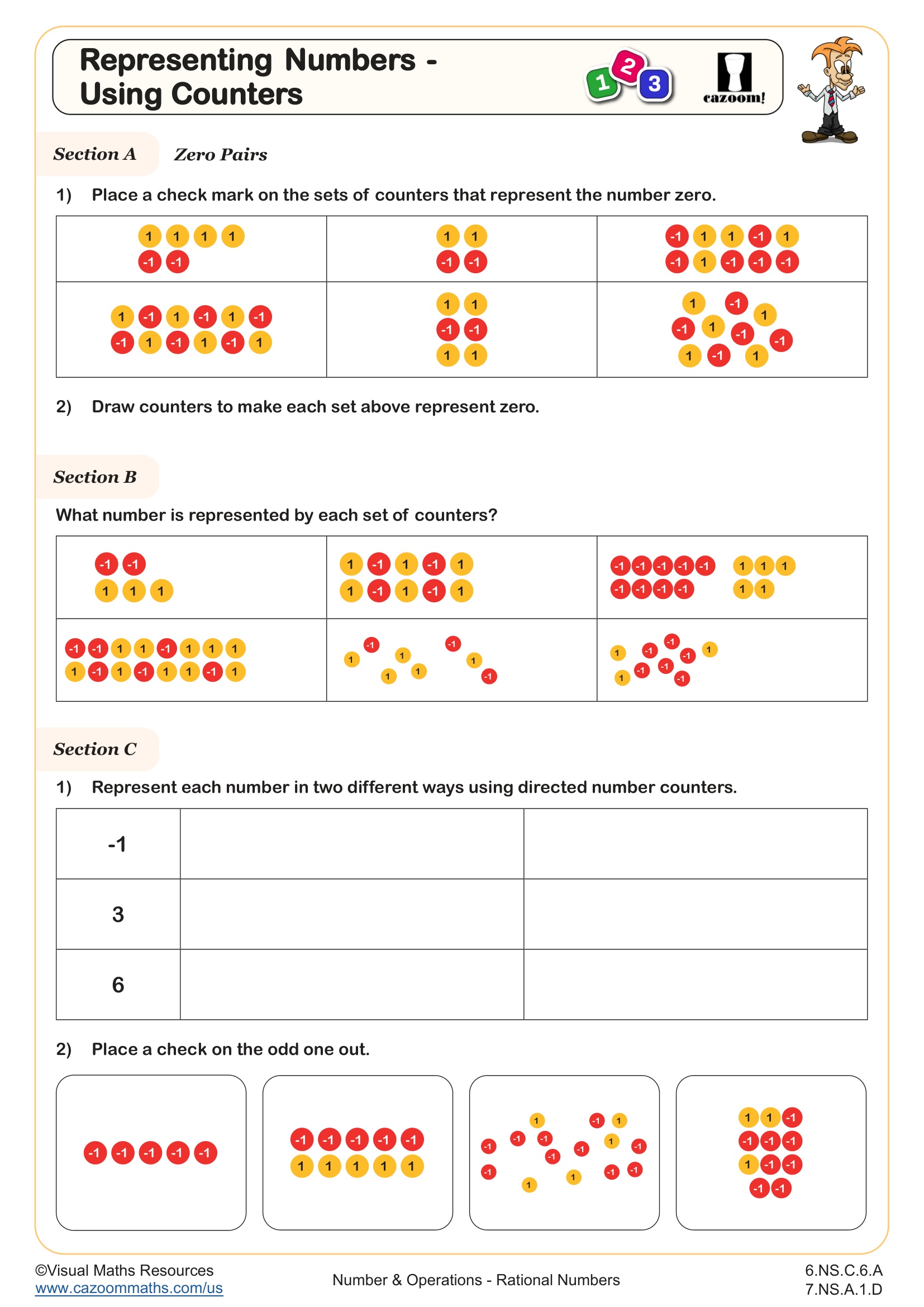
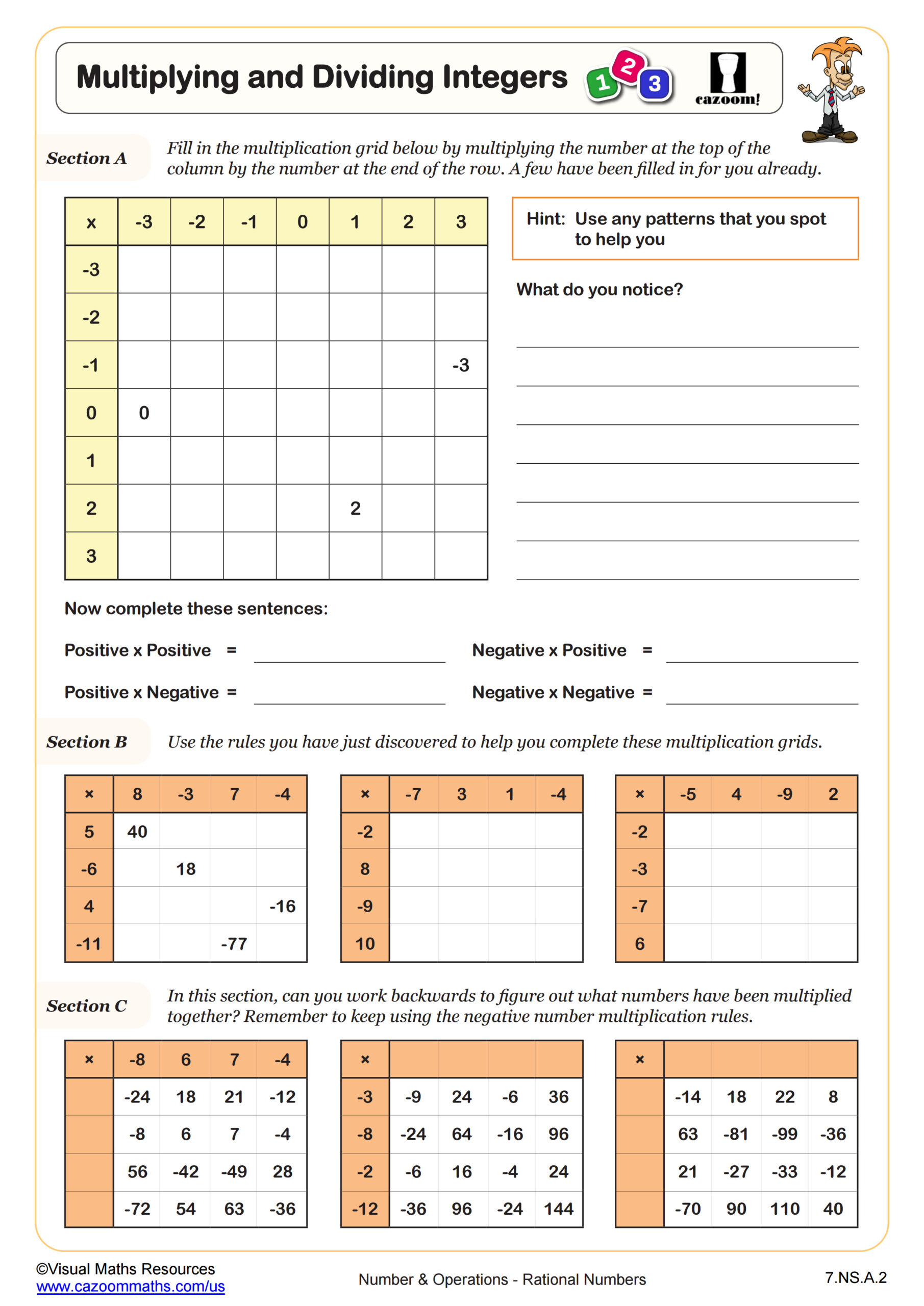
Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (–1)(–1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts

Multiplication Using Number Counters WORKSHEET DESCRIPTION

Using number counters allows students to see the impact of multiplying positive and negative numbers, helping them understand that a negative multiplied by a positive or vice versa results in a negative product, as well as differentiating between the magnitude and direction of numbers in multiplication.

Throughout this worksheet learners will: match arrays to calculations, look at the commutative nature of multiplication, draw arrays to aid them in completing multiplication number sentences, discover patterns in multiplication of positive and negative numbers, use these patterns to complete number sentences where arrays would be inappropriate, and complete puzzles involving the multiplication of a positive and negative number.

Multiplication Using Number Counters Worksheet Suitable for Students in 7th Grade and 7th Grade

RELATED TO Multiplication Using Number Counters WORKSHEET

Subtracting Integers with Counters

Grades: 7th Grade

Preview of Subtracting Integers with Counters

Finding the Difference - Directed Numbers

Grades: 7th Grade

Preview of Finding the Difference - Directed Numbers

Representing Numbers - Using Counters

Grades: 6th Grade, 7th Grade

Preview of Representing Numbers - Using Counters

Multiplying and Dividing Integers

Grades: 7th Grade

Preview of Multiplying and Dividing Integers

Frequently Asked Questions

This multiplication using number counters worksheet is designed for students in 7th Grade and aligns with Common Core State Standards.