Loading...
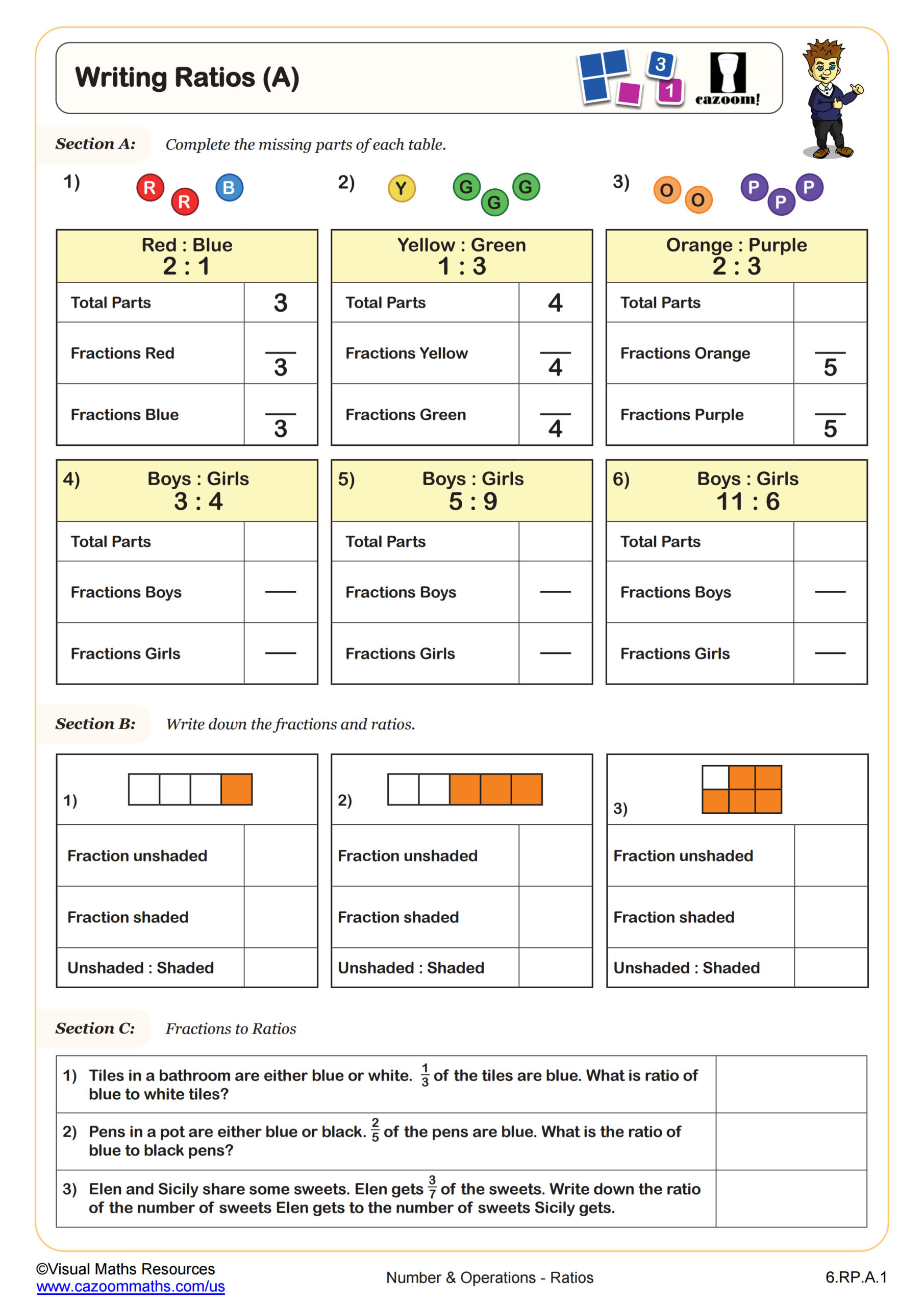
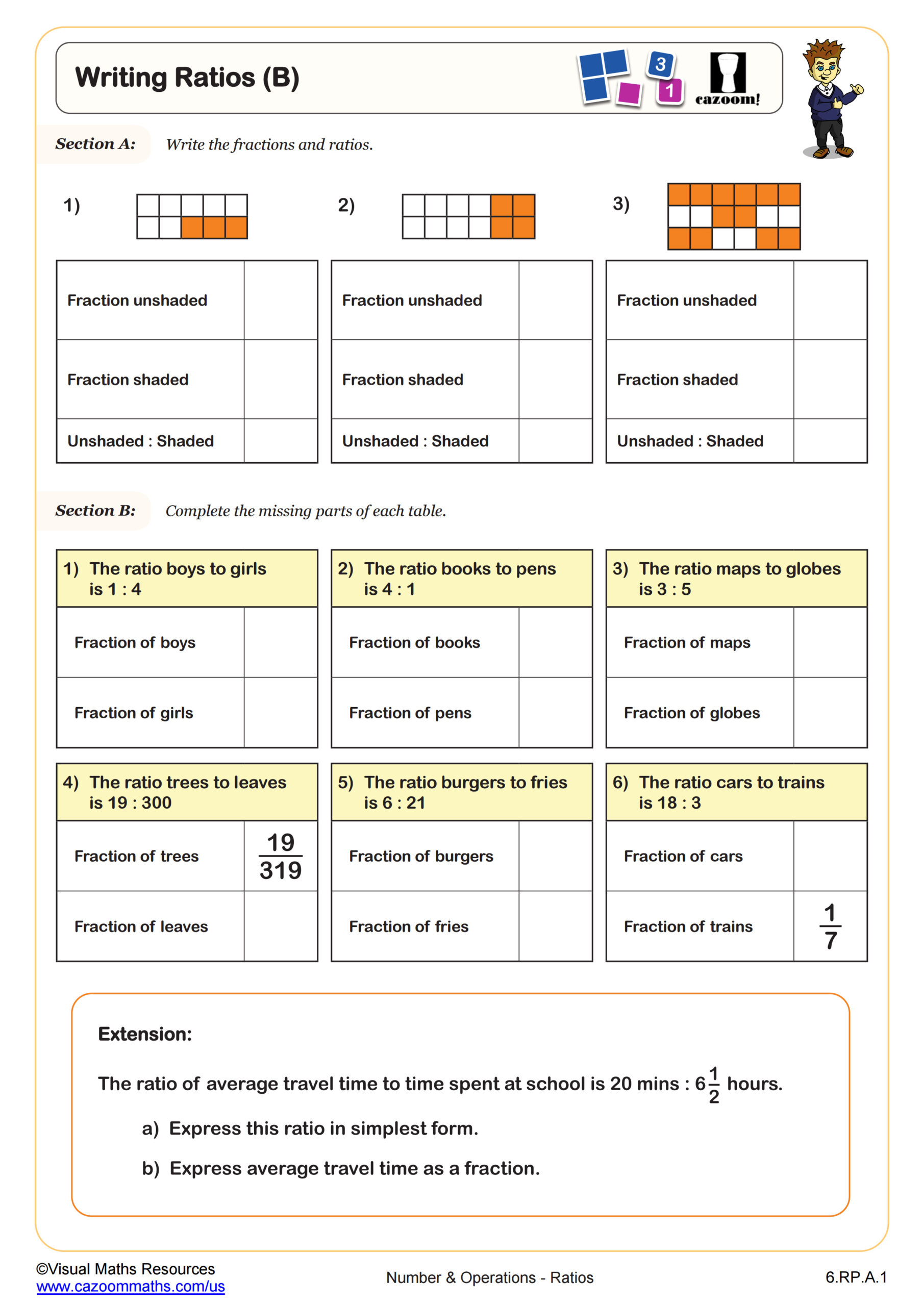
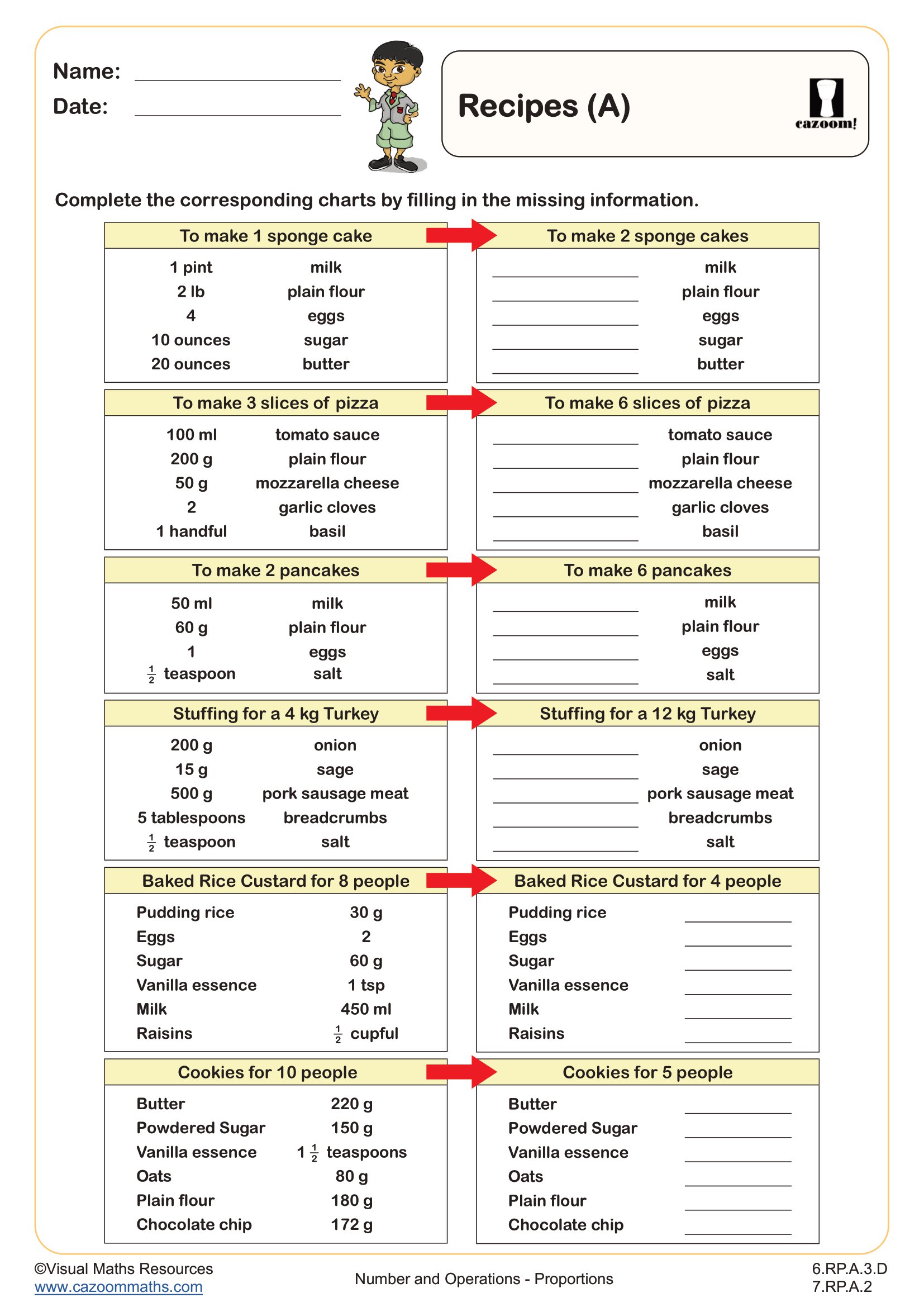
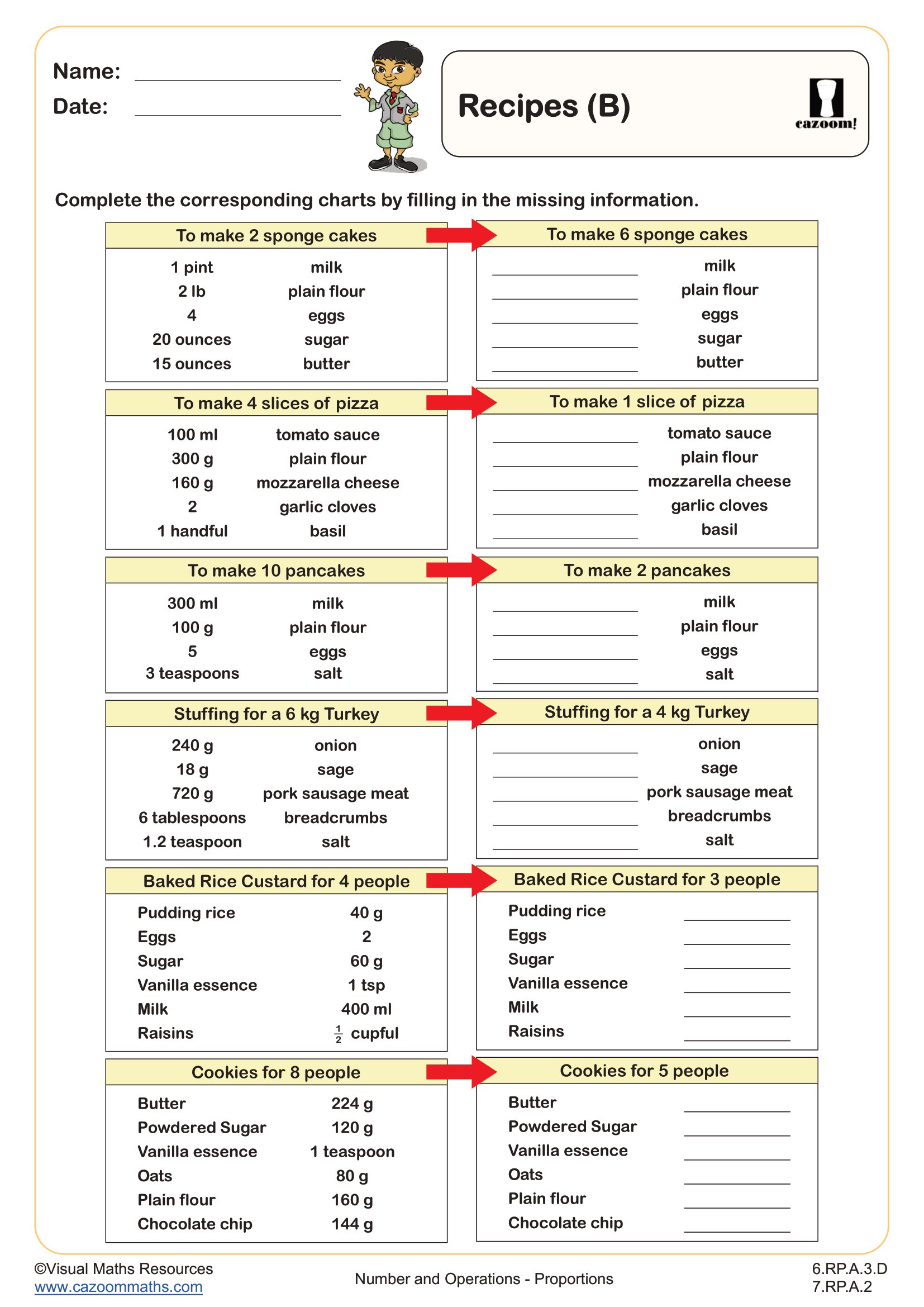
Back to:
Recipes (B) WORKSHEET
Suitable for Grades: 6th Grade, 7th Grade
CCSS: 6.RP.A.3.D, 7.RP.A.2
CCSS Description: Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
Recognize and represent proportional relationships between quantities. a. Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin. b. Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships. c. Represent proportional relationships by equations. For example, if total cost t is proportional to the number n of items purchased at a constant price p, the relationship between the total cost and the number of items can be expressed as t = pn. d. Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.
Recognize and represent proportional relationships between quantities. a. Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin. b. Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships. c. Represent proportional relationships by equations. For example, if total cost t is proportional to the number n of items purchased at a constant price p, the relationship between the total cost and the number of items can be expressed as t = pn. d. Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.
Recipes (B) WORKSHEET DESCRIPTION
Recipe problems are the perfect conceptual introduction to proportion for many learners. They remain ever popular with SATs exams and let’s face it, form an important life skill!
In this worksheet students have 6 recipe cards that need scaling by integer and fractional scale factors. Examples include recipes from 4 to 1 and 8 to 5.
Metric and imperial units are used which is an opportunity for discussion with pupils.
Your learners will be faced with challenges such as 3 ÷ 5 and should be encouraged to complete this worksheet without a calculator.
