Menu

BY TOPICBY CCSS
SCHOOLSSEARCH
LOGINFREE TRIAL
Back to:
Percentages

Reverse Percentages - Using a Bar Model (B) WORKSHEET

Suitable for Grades: 7th Grade
CCSS: 7.RP.A.2, 7.RP.A.3
CCSS Description: Recognize and represent proportional relationships between quantities. a. Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin. b. Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships. c. Represent proportional relationships by equations. For example, if total cost t is proportional to the number n of items purchased at a constant price p, the relationship between the total cost and the number of items can be expressed as t = pn. d. Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.

Use proportional relationships to solve multistep ratio and percent problems, including simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, and percent error.

Reverse Percentages - Using a Bar Model (B) WORKSHEET DESCRIPTION

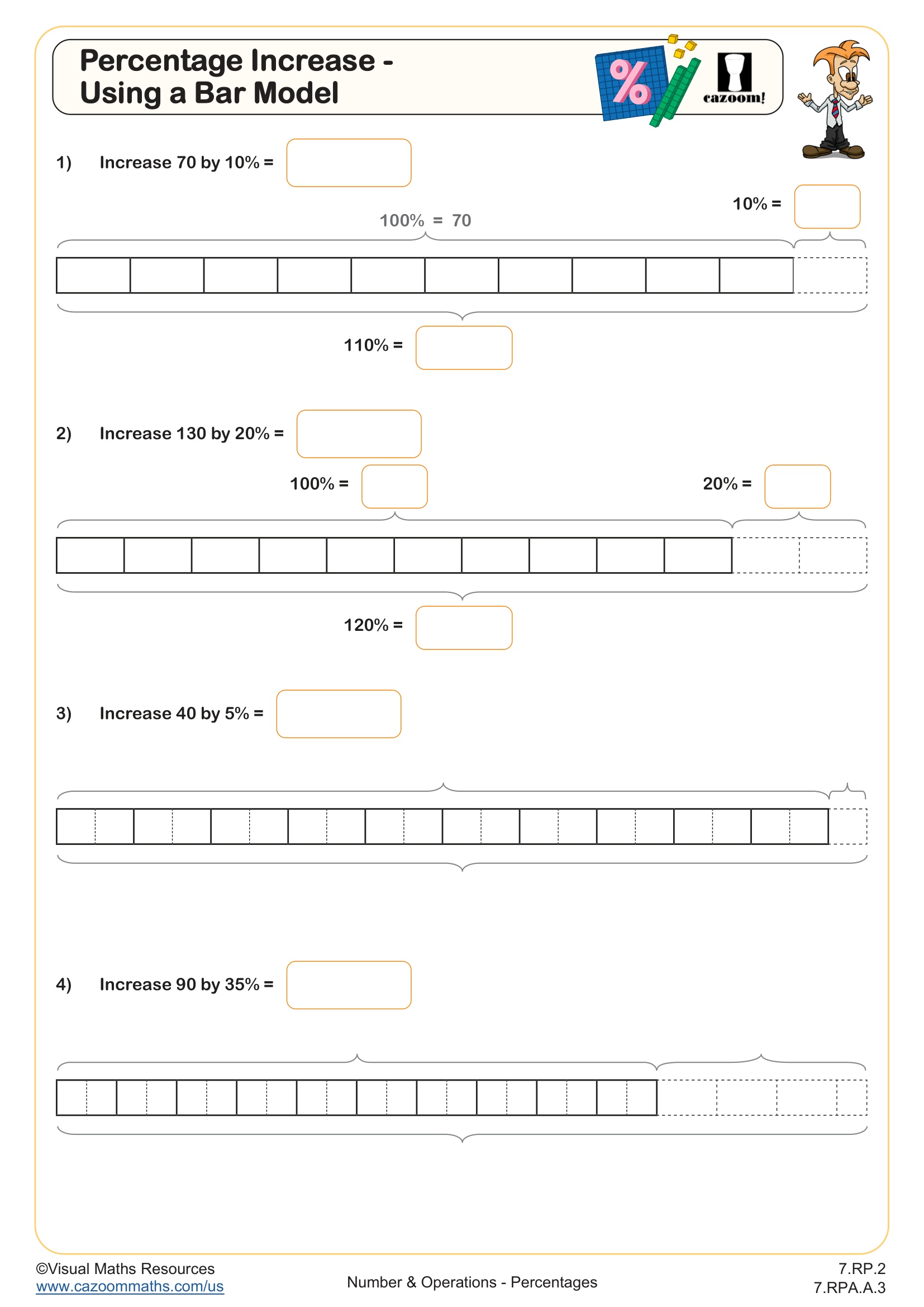
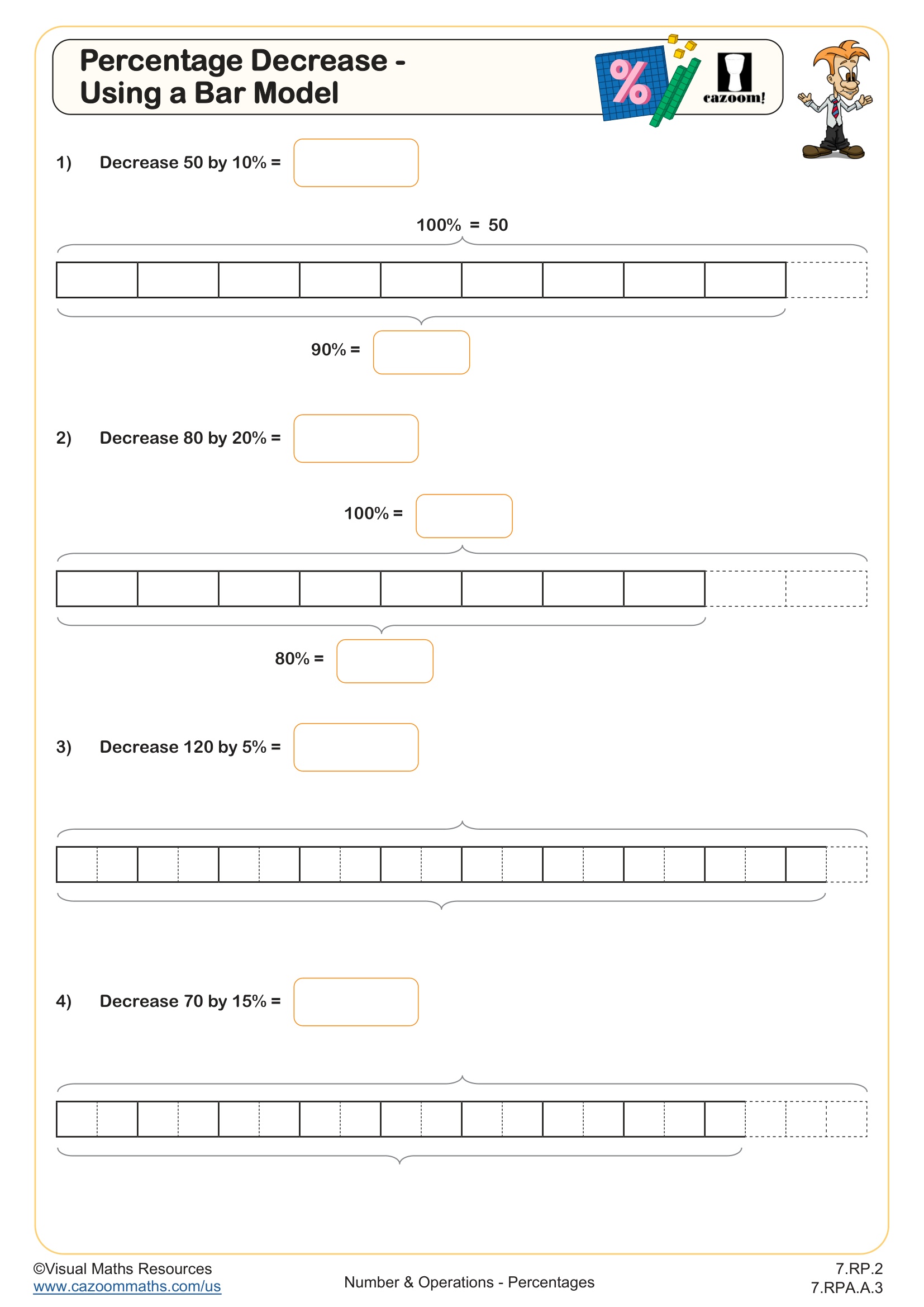
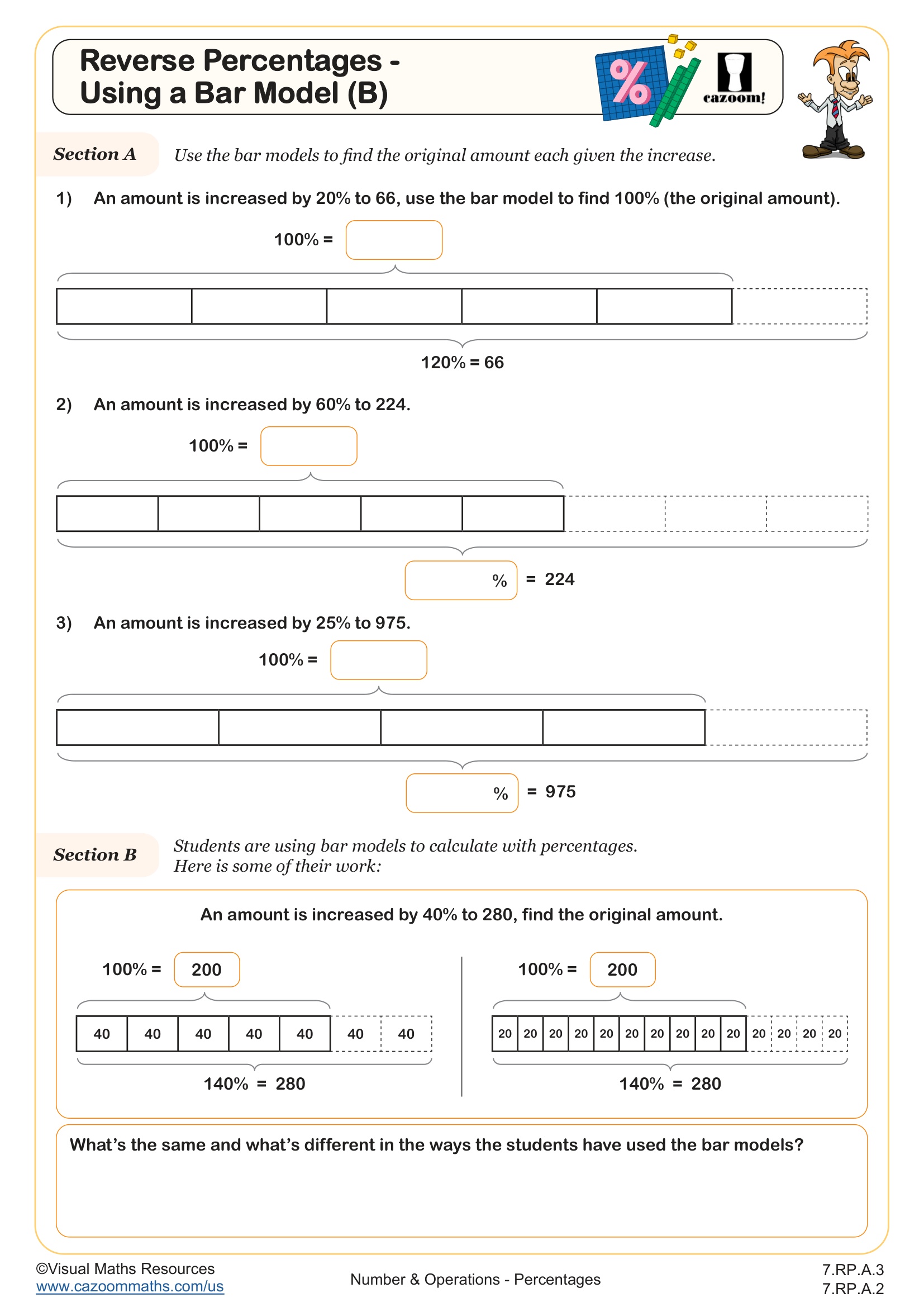
This worksheet provides an excellent introduction to finding the original amount when it has been subjected to a percentage increase. Bar models provide a visual tool for understanding percentages and help bridge the gap between concrete, pictorial, and abstract concepts.

All percentage increases are multiples of 5% and the different sections are structured with a decreasing level of scaffolding.

Section B provides an opportunity for students to articulate their understanding as they discuss what is the same and what's different between two different uses of the bar model for finding 100% after a 40% increase.

Reverse Percentages - Using a Bar Model (B) Worksheet Suitable for Students in 7th Grade

RELATED TO Reverse Percentages - Using a Bar Model (B) WORKSHEET

Percentage Increase - Using a Bar Model

Grades: 7th Grade, IM 1

Preview of Percentage Increase - Using a Bar Model

Percentages of Amounts - Using a Tape Diagram (A)

Grades: 6th Grade

Preview of Percentages of Amounts - Using a Tape Diagram (A)

Percentage Decrease - Using a Bar Model

Grades: 7th Grade, IM 1

Preview of Percentage Decrease - Using a Bar Model

Percentages of Amounts - Using a Tape Diagram (B)

Grades: 6th Grade

Preview of Percentages of Amounts - Using a Tape Diagram (B)

Frequently Asked Questions

This reverse percentages - using a bar model (b) worksheet is designed for students in 7th Grade and aligns with Common Core State Standards.