Back to:

Solving Linear Simultaneous Equations - Change One Equation WORKSHEET

Suitable for Grades: 8th Grade, Algebra I, IM 1

CCSS: 8.EE.C.8, HSA.REI.C.5

CCSS Description: a. Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously. b. Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6. c. Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair.

Prove that, given a system of two equations in two variables, replacing one equation by the sum of that equation and a multiple of the other produces a system with the same solutions.

Solving Linear Simultaneous Equations - Change One Equation WORKSHEET DESCRIPTION

Perfect for beginning to solve simultaneous equations, this worksheet consists of systems of equations where one coefficient is a multiple of another for at least one variable.

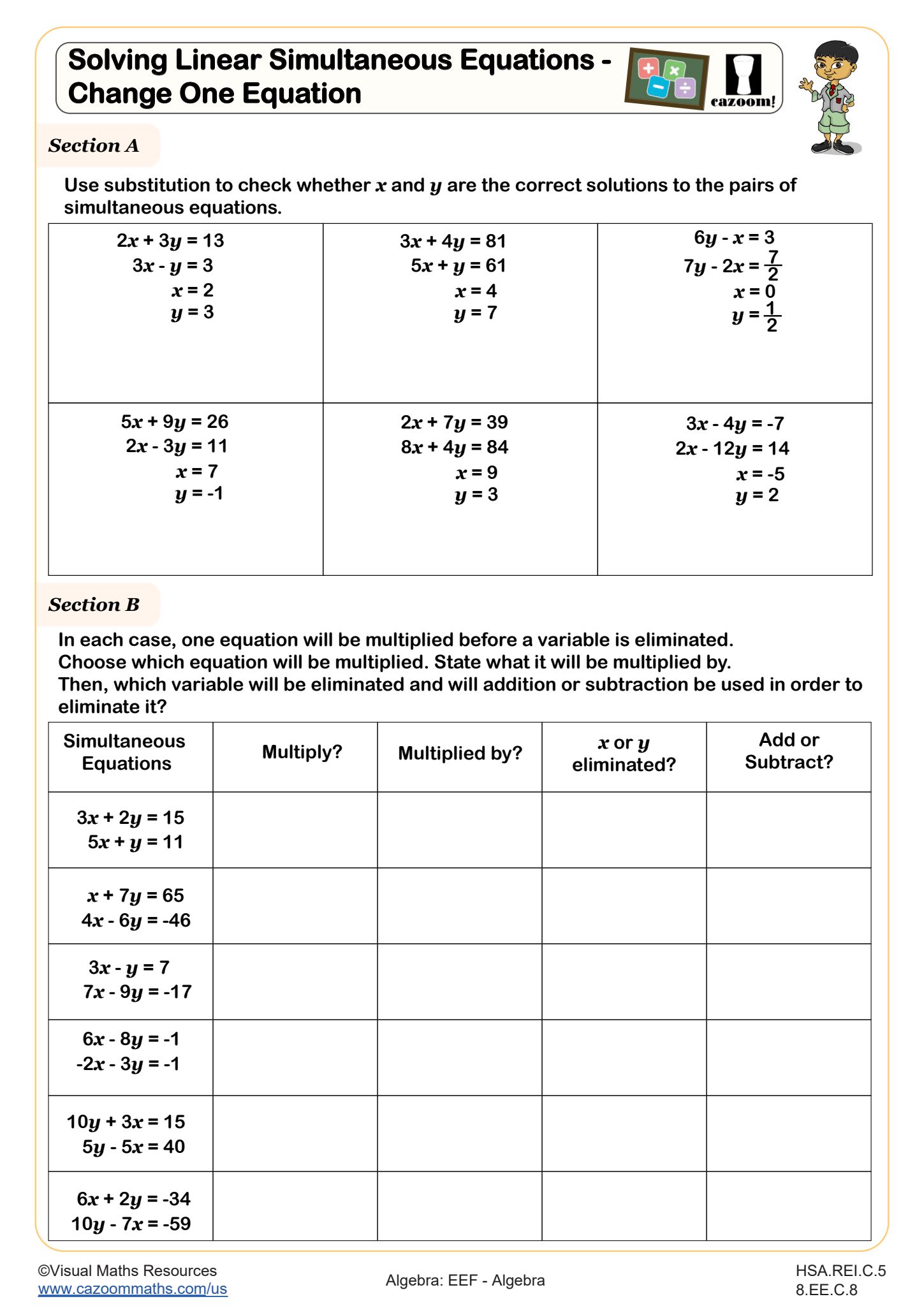
Section A acts as a warm up as students use substitution to check whether given values are the correct solutions to six pairs of equations.

In Section B, learners will decide: which equation to multiply, what it should be multiplied by, which variable should be eliminated and whether addition or subtraction should be used in order to eliminate it in a further six pairs of equations.

Students will solve 8 systems of simultaneous equations in Section C. Solutions are a mix of positive and negative values, and most are integers.

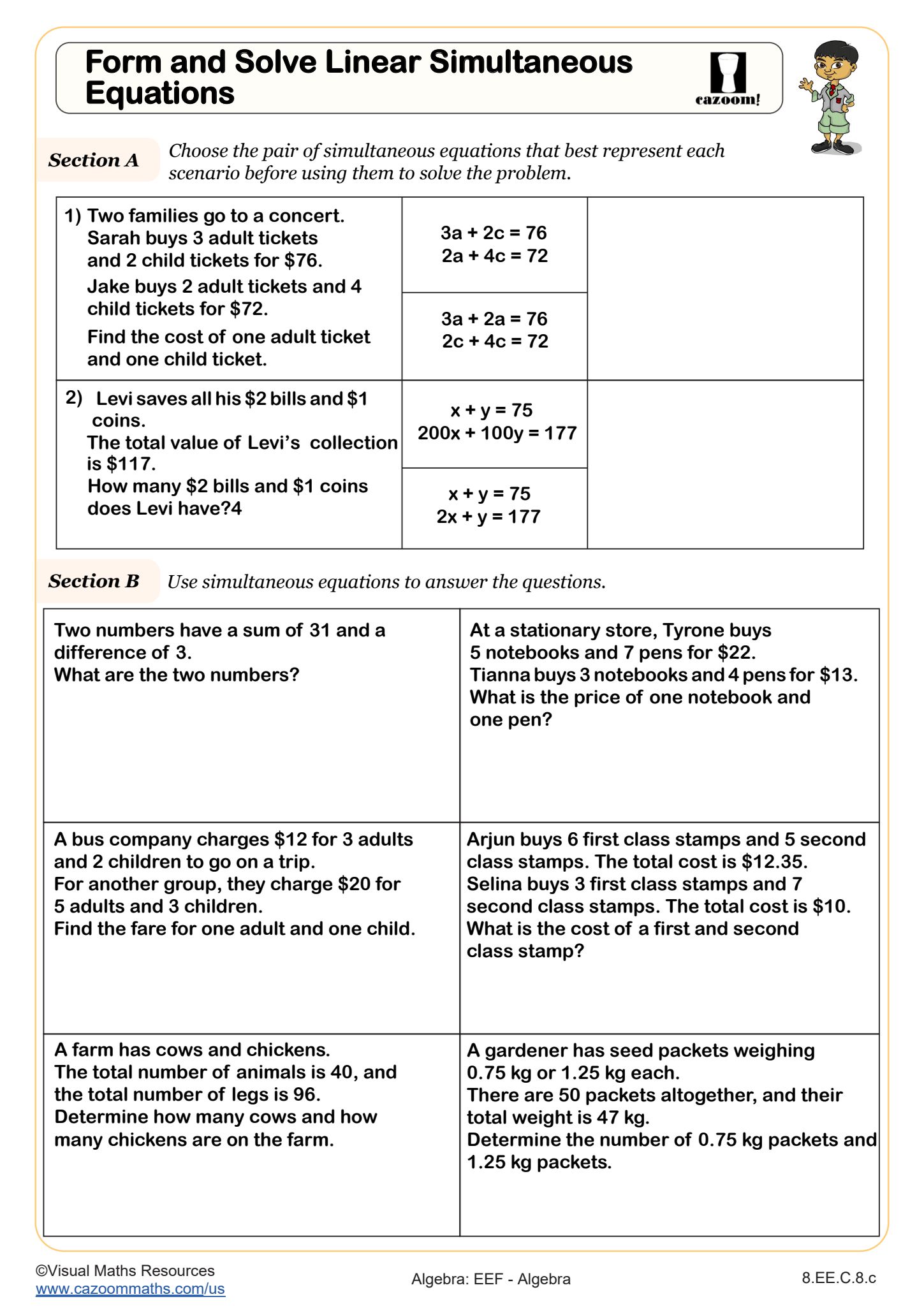
Lastly, Section D asks students to form and solve a pair of simultaneous equations in order to solve a worded problem.