3rd Grade 2D Shapes Worksheets
What are 2D shapes and why do 3rd graders study them?
2D shapes are flat figures with length and width but no depth, including polygons like triangles, quadrilaterals, pentagons, and hexagons. In 3rd grade, students move beyond simply naming shapes to analyzing their properties, such as counting sides and vertices, identifying parallel and perpendicular lines, and understanding what makes a polygon regular versus irregular. This work aligns with Common Core standards that require students to reason with shapes and their attributes.
Students frequently confuse the terms "side" and "edge" when describing 2D shapes, often calling the boundary an edge rather than a side. Teachers find that having students physically trace each side while counting helps reinforce correct terminology. Understanding 2D shapes prepares students for area and perimeter calculations in later grades and develops the visual-spatial skills needed for geometry throughout their education.
What should 3rd graders know about 2D shapes?
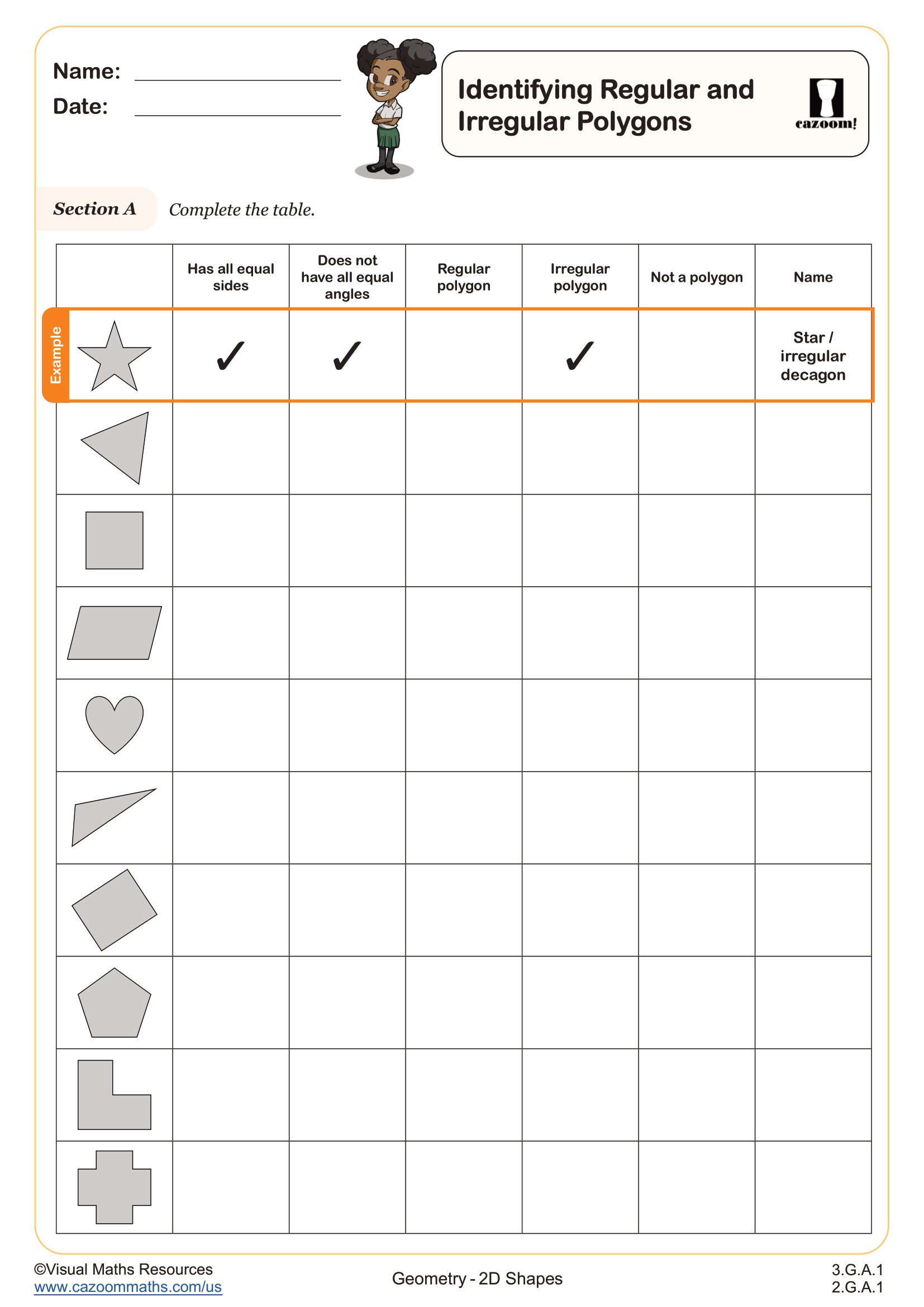
By 3rd grade, students should confidently identify common polygons by name and recognize their defining characteristics. They should understand that polygons are closed figures made of straight sides, distinguish between regular polygons (equal sides and angles) and irregular polygons, and classify quadrilaterals into more specific categories like rectangles, squares, rhombuses, and trapezoids. Students also learn to identify right angles within shapes and recognize parallel sides.
This work builds directly on 1st and 2nd grade shape recognition, where students learned basic shape names and simple attributes. The 3rd grade focus on regular versus irregular polygons and detailed property analysis creates the foundation for 4th grade work with lines of symmetry and angle measurement. Many teachers notice that students who master shape classification in 3rd grade approach fraction concepts more confidently, since partitioning shapes requires strong spatial understanding.
How do students distinguish between regular and irregular polygons?
A regular polygon has all sides of equal length and all angles of equal measure, while an irregular polygon has sides or angles that differ in size. Students learn to examine shapes systematically by measuring or comparing side lengths and checking whether angles appear equal. For example, a square is a regular quadrilateral because all four sides and all four angles are identical, while a rectangle with different length and width measurements is irregular. Teachers often see students make breakthroughs when they use rulers to verify whether sides are truly equal rather than relying on visual estimation alone.
This distinction appears frequently in architecture and design. Honeycomb structures use regular hexagons because equal sides create strong, space-efficient patterns. Road signs employ regular polygons (stop signs are regular octagons) for instant recognition from any angle. Engineers choose between regular and irregular shapes based on structural needs, making this seemingly abstract math concept a practical tool in STEM fields.
How can teachers use these 2D shapes worksheets effectively?
These worksheets provide structured practice that helps students apply geometric vocabulary and recognition skills with increasing independence. The activities move from identification tasks, where students classify shapes based on given properties, to creation tasks, where they draw shapes following specific requirements. This progression allows teachers to assess whether students truly understand shape attributes or are simply memorizing names without grasping underlying characteristics.
Many teachers use these worksheets during math centers, pairing them with hands-on materials like pattern blocks or geoboards so students can manipulate physical shapes before completing paper tasks. The answer keys make these worksheets valuable for independent practice during intervention time or as homework assignments, since students can self-check their understanding. They also work well as quick assessments before and after instruction to measure growth in geometric reasoning skills.