3rd Grade Lines and Angles Worksheets
What Lines and Angles Concepts Do 3rd Graders Learn?
Third grade students learn to identify and draw points, lines, line segments, rays, and angles as part of the Common Core State Standards for geometry. They classify shapes by analyzing their sides and angles, understanding attributes like parallel lines, perpendicular lines, and right angles. This foundational vocabulary becomes the language students use to describe and compare two-dimensional figures throughout their math education.
Students often confuse line segments with lines, forgetting that lines extend infinitely in both directions while line segments have two endpoints. Teachers find that using real-world examples helps clarify these distinctions: a line segment might represent the edge of a desk, while a line models a road that continues beyond what we can see. When students connect geometric terms to tangible objects in their classroom and community, the abstract concepts become more concrete and memorable.
How Does Lines and Angles Fit Into 3rd Grade Math Standards?
In 3rd grade, lines and angles instruction builds directly on the shape recognition and basic geometry from 1st and 2nd grades. Students move beyond simply naming shapes to analyzing their properties and understanding how geometric attributes define categories. This shift represents an important transition from concrete observation to mathematical reasoning, as students explain why a square is also a rectangle based on its angles and parallel sides.
This geometry foundation prepares students for 4th grade work with symmetry, angle measurement, and classifying triangles and quadrilaterals by specific angle measures. The language and concepts learned in 3rd grade become tools for more precise geometric thinking in upper elementary. Students who solidify their understanding of perpendicular and parallel lines in 3rd grade find angle classification and protractor use significantly easier in later grades.
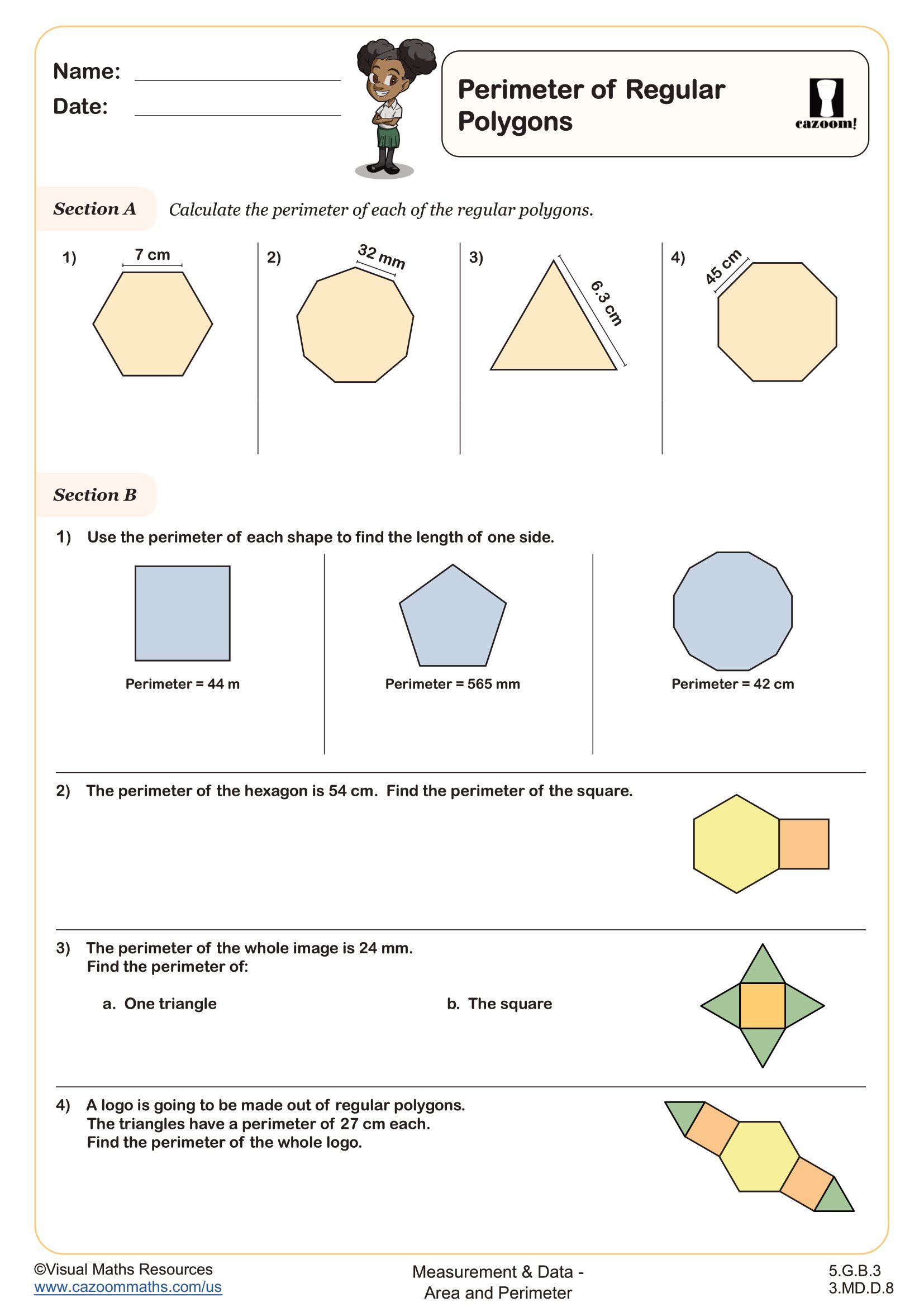
How Do Lines and Angles Connect to Perimeter?
Understanding the sides and angles of polygons provides the foundation for calculating perimeter accurately. When students recognize that regular polygons have equal side lengths and equal angles, they can use multiplication as a shortcut instead of adding each side individually. For a regular hexagon with 4-inch sides, students learn that 6 × 4 gives the same result as 4 + 4 + 4 + 4 + 4 + 4, connecting geometry to their multiplication skills.
Architects and landscape designers use these perimeter concepts when planning fenced areas, garden borders, or building foundations. A landscape architect designing a hexagonal patio needs to calculate the perimeter to determine how much edging material to purchase. Construction workers frame regular polygon-shaped structures by understanding that equal angles create equal sides, ensuring their measurements stay consistent around the entire shape. These real-world applications show students why geometric properties matter beyond the classroom.
How Can Teachers Use These Lines and Angles Worksheets?
These worksheets provide structured practice that connects geometric vocabulary to measurement applications, helping students see how identifying shape properties leads to solving problems. The problems progress from recognizing regular polygons to calculating their perimeters, scaffolding student thinking from identification to computation. Answer keys allow teachers to quickly assess whether students are correctly identifying the number of sides and applying the correct operation.
Many teachers use these worksheets during math centers or as follow-up practice after introducing perimeter concepts with manipulatives. They work well for students who need additional reinforcement with regular polygon properties or as homework to build fluency before assessments. The visual nature of polygon problems helps struggling learners, while the computational aspect challenges students to apply multiple skills simultaneously. Teachers often assign these during intervention time to target specific gaps in geometry understanding.