4th Grade Decimals Worksheets
What Are the Key Decimal Concepts for 4th Grade?
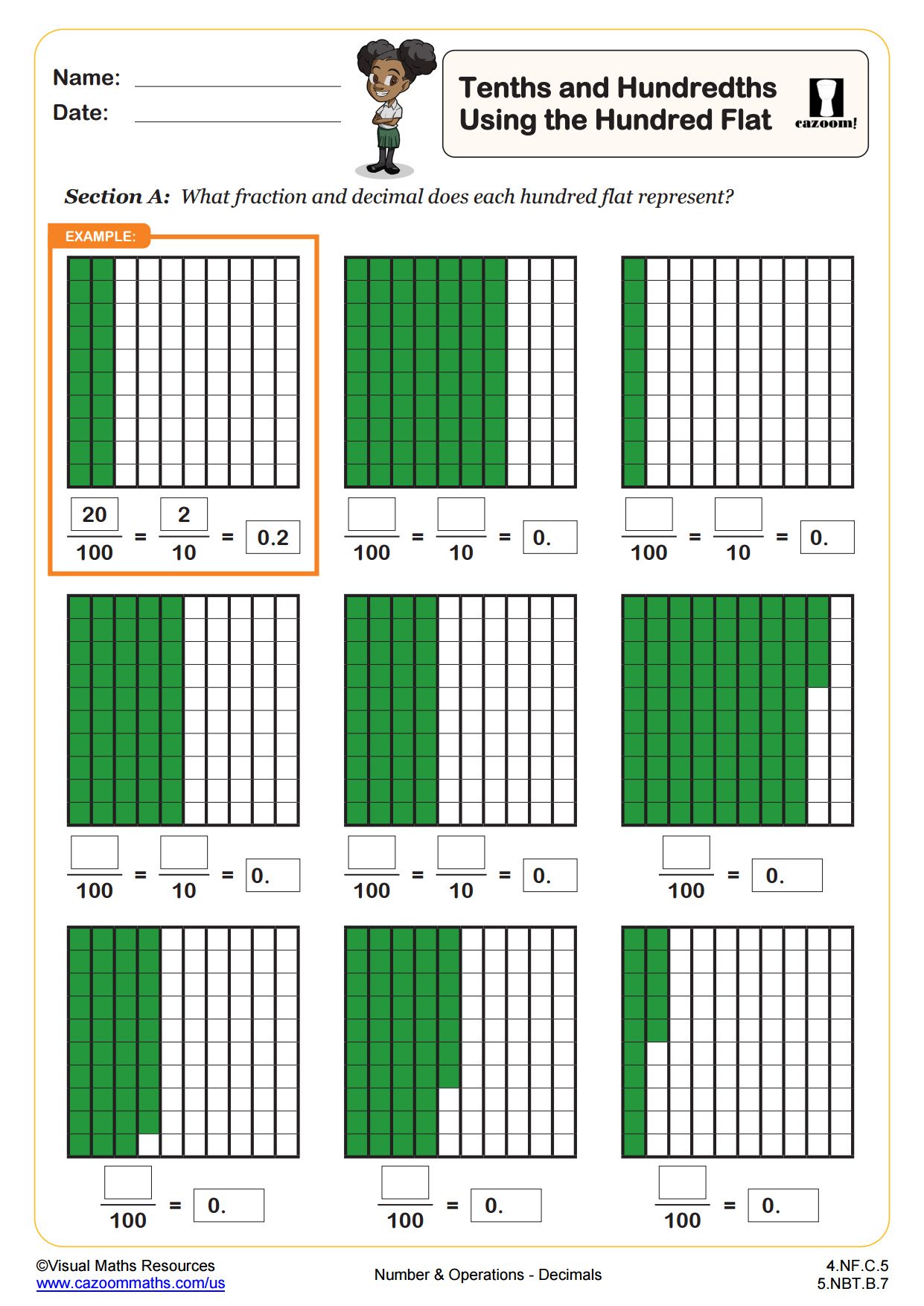
Fourth grade students focus on understanding decimals as representations of fractions with denominators of 10 and 100. The curriculum emphasizes reading and writing decimals to hundredths, using decimal notation for fractions with denominators of 10 or 100, and comparing decimal values based on place value understanding. Students also work with visual models like hundred flats and number lines to develop concrete understanding before moving to abstract notation.
A common misconception occurs when students treat decimals like whole numbers and assume that 0.25 is greater than 0.3 because 25 is larger than 3. Teachers frequently address this by having students shade hundred flats to visualize that 0.3 (or 30 hundredths) covers more area than 0.25. This visual connection helps students understand that place value matters more than the number of digits after the decimal point.
What Should 4th Graders Know About Decimals?
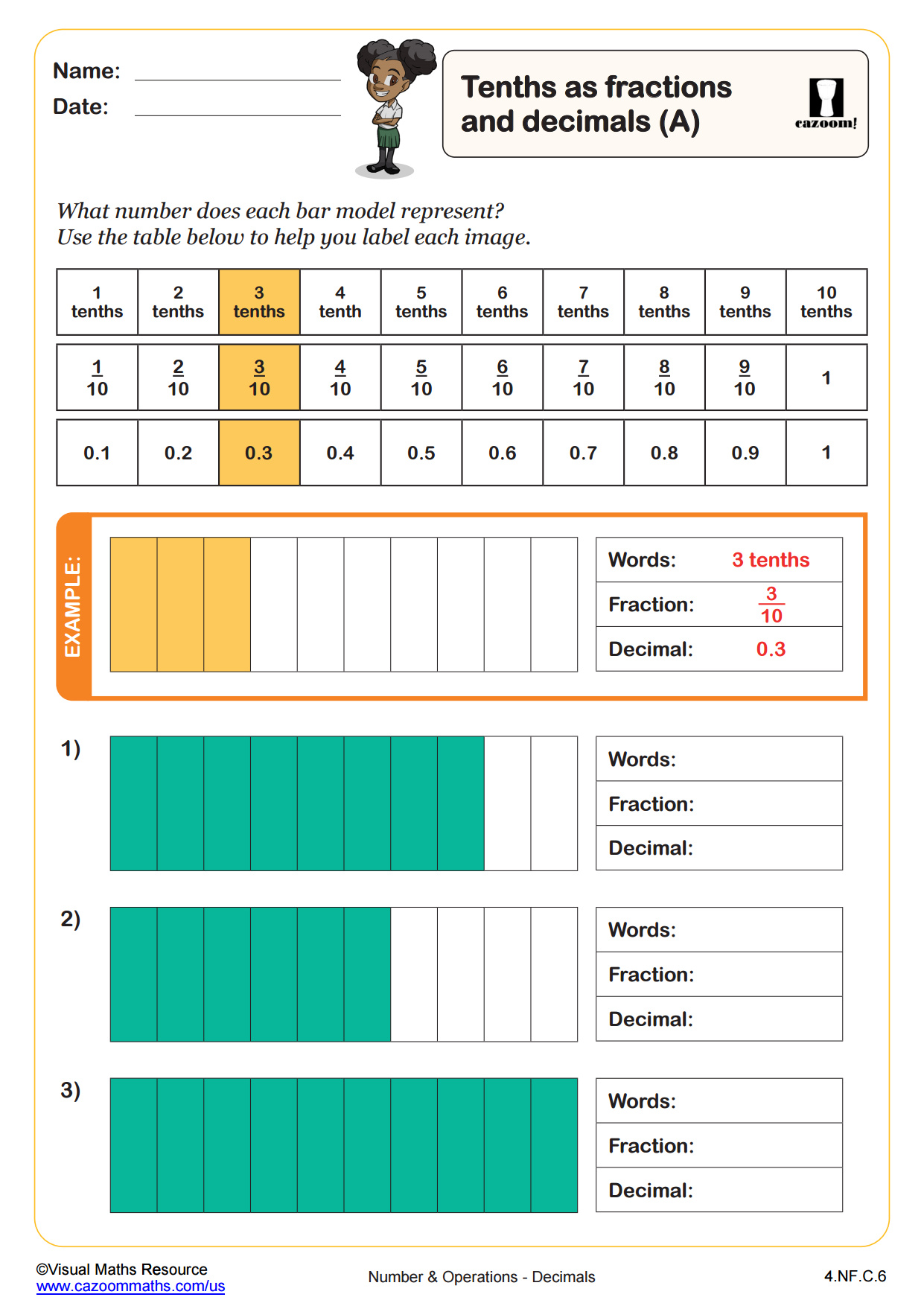
By the end of 4th grade, students should confidently read decimals to hundredths, write them in multiple forms (0.7, 7/10, seven tenths), and compare decimal values using place value reasoning. They should recognize equivalent decimals like 0.5 and 0.50, understand that the decimal point separates whole numbers from fractional parts, and use models to represent decimal quantities. State assessments typically include problems asking students to identify decimal locations on number lines and convert between fraction and decimal notation.
This work builds directly on 3rd grade fraction understanding, particularly comparing fractions with the same denominator and recognizing fractions on number lines. The decimal foundation established in 4th grade becomes critical in 5th grade when students begin adding, subtracting, multiplying, and dividing decimals. Students who master the fraction-decimal connection in 4th grade typically show greater confidence with decimal operations later.
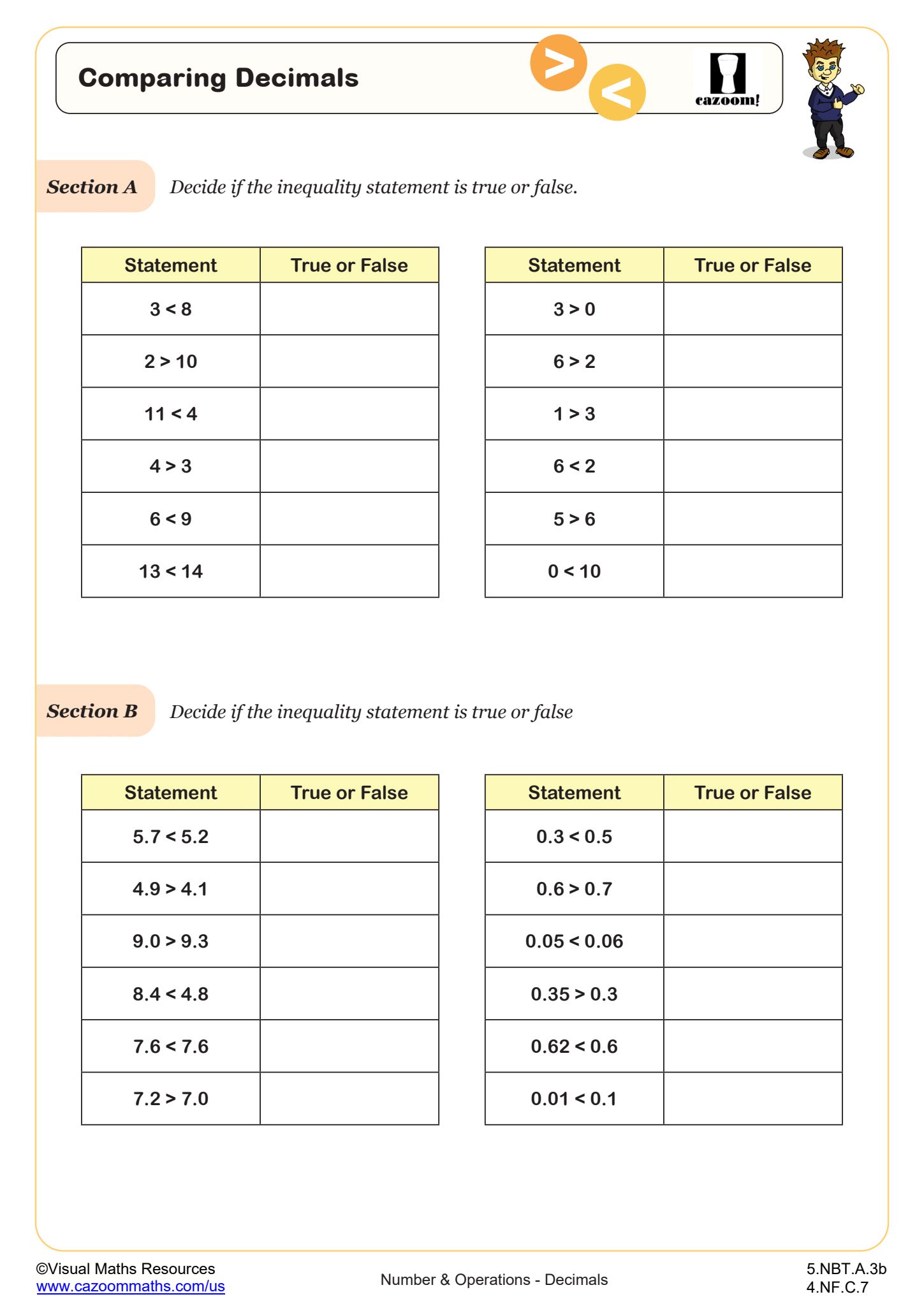
How Do Students Learn to Compare Decimals?
Comparing decimals requires students to align place values and compare digits systematically from left to right, starting with the tenths place and moving to hundredths. Teachers introduce comparison strategies by having students write decimals with the same number of decimal places (adding zeros as placeholders), then comparing as they would whole numbers. Visual models like hundred flats or number lines help students see which decimal quantity is actually larger before they develop the abstract algorithm.
This skill connects directly to real-world applications in measurement and money. Students encounter decimal comparisons when reading temperatures (which is colder: 98.4°F or 98.7°F?), measuring ingredients in recipes (0.75 cups versus 0.5 cups), or comparing prices ($3.45 versus $3.54). In STEM contexts, scientists and engineers constantly compare decimal measurements in data analysis, making this an authentic skill beyond the classroom.
How Can Teachers Use These Decimal Worksheets Effectively?
These worksheets provide scaffolded practice moving from concrete representations to abstract understanding. The activities incorporating hundred flats and visual models work well early in a decimal unit to build conceptual understanding, while comparison and conversion worksheets strengthen procedural fluency once students grasp the underlying concepts. The answer keys allow for immediate feedback, helping students identify errors in their reasoning before misconceptions become ingrained.
Many teachers use these worksheets during small group instruction to differentiate based on student readiness, assigning the tenths-focused activities to students still building foundational understanding while giving comparison tasks to students ready for challenge. The worksheets also serve as effective homework assignments that parents can support using the answer keys, or as intervention materials for students who need additional practice beyond classroom instruction. Paired work allows students to discuss their reasoning and catch each other's errors in real time.