5th Grade Functions Worksheets
What Are Functions in 5th Grade Math?
In 5th grade, functions appear as patterns where one quantity depends on another in a predictable way. Students explore these relationships through input-output tables, coordinate graphs, and visual models like stacked number lines. The focus remains on recognizing and describing patterns rather than using formal function notation, which appears later in middle school.
Direct proportion represents the most accessible type of function for elementary students. When exploring relationships like "gallons of paint needed for square feet of wall" or "total cost based on number of items," students discover multiplicative relationships where doubling the input doubles the output. A common error occurs when students confuse additive patterns with multiplicative ones, expecting the output to increase by the same amount rather than the same factor.
How Do 5th Grade Function Standards Build Mathematical Understanding?
Fifth graders work with two numerical patterns and identify relationships between corresponding terms, according to Common Core Standard 5.OA.B.3. Students generate these patterns using given rules, graph ordered pairs on coordinate planes, and explain how terms in one sequence relate to terms in another. This work directly extends their understanding of operations and prepares them for ratios in 6th grade.
This learning builds on 4th grade work with number patterns and multiples while laying groundwork for proportional reasoning in middle school. Students who recognize functional relationships in 5th grade transition more smoothly to formal equations like y = mx in 6th and 7th grades. The visual representation skills developed here become particularly valuable when students later encounter slope and linear relationships in algebra.
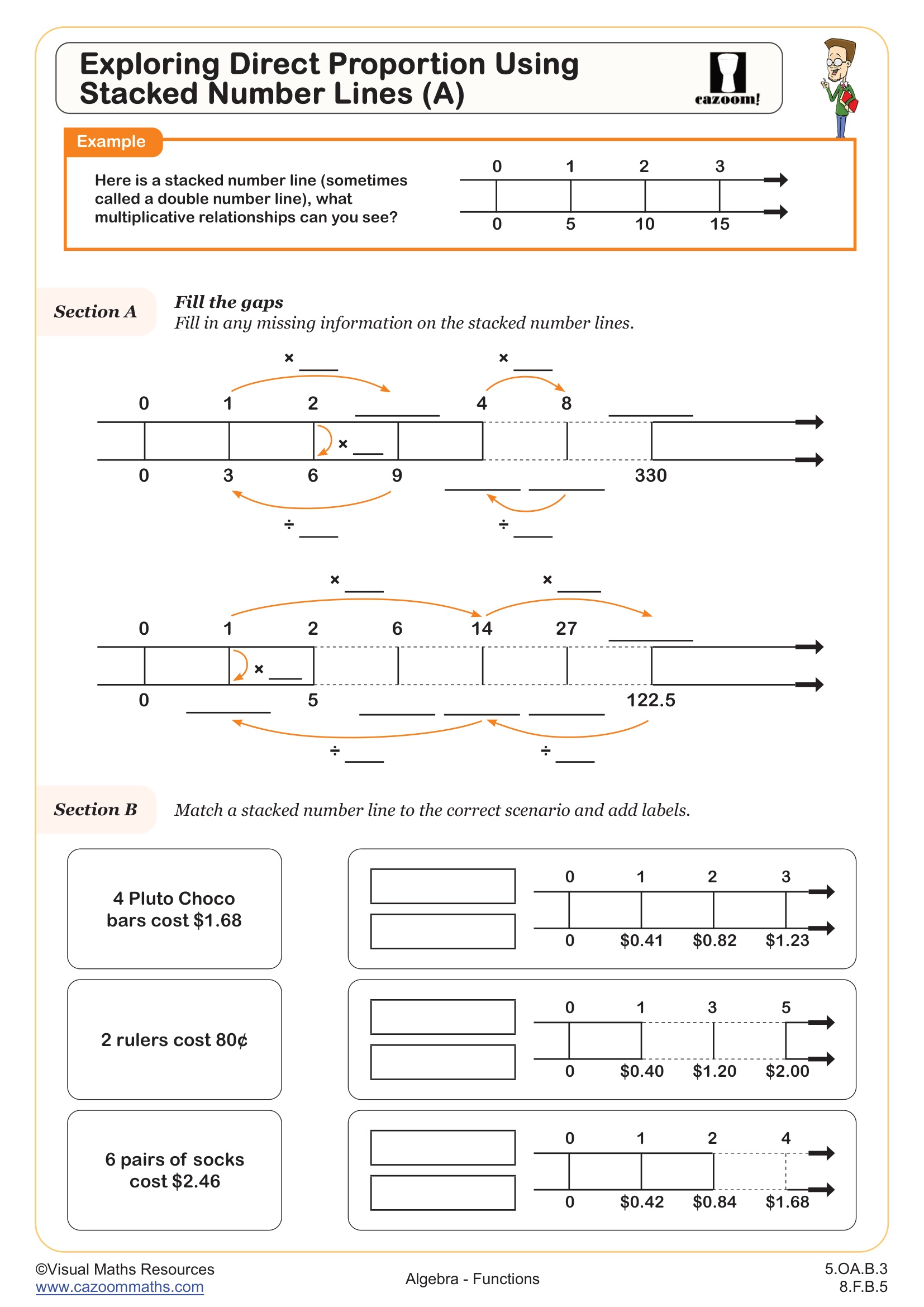
What Makes Stacked Number Lines Effective for Teaching Proportional Relationships?
Stacked number lines display two related quantities simultaneously, with one number line positioned directly above the other so corresponding values align vertically. This arrangement helps students see the constant multiplicative relationship between quantities. For example, one line might show hours (1, 2, 3, 4) while the line above shows miles traveled (55, 110, 165, 220), making the rate of 55 miles per hour visually apparent.
This visualization connects directly to STEM applications students encounter daily. Understanding proportional relationships helps students calculate cooking measurements when doubling recipes, determine costs when buying multiple items, or figure out how long a road trip will take at constant speed. Engineers use this same proportional thinking when scaling blueprints, and scientists apply it when converting between units or analyzing experimental data where one variable depends consistently on another.
How Can Teachers Use These Function Worksheets Most Effectively?
These worksheets guide students through structured exploration of proportional relationships using visual models before moving to numerical reasoning. The stacked number line format provides concrete support for students who struggle with abstract pattern recognition. Having two versions (A and B) allows teachers to differentiate instruction or provide additional practice on the same concept without simple repetition.
Many teachers use these worksheets during small group instruction to identify which students grasp the multiplicative nature of proportional relationships versus those still thinking additively. The answer keys make these materials practical for independent work stations, homework assignments, or intervention sessions where students need extra support before tackling more complex function problems. Paired work also proves effective, with partners explaining to each other why corresponding values maintain the same ratio throughout the relationship.