5th Grade Lines and Angles Worksheets
What Are the Main Concepts in 5th Grade Lines and Angles?
Fifth graders work with acute, obtuse, right, and straight angles, learning to classify them by their measures. Students also study parallel lines (lines that never intersect), perpendicular lines (lines that meet at 90-degree angles), and intersecting lines. The curriculum introduces angle measurement using protractors and connects these concepts to polygon properties, particularly regular polygons where all sides and angles are equal.
A common error occurs when students confuse the angle with the length of its rays. Many students initially believe that longer rays create larger angles, when angle size depends entirely on the amount of rotation between the rays. Teachers often use folded paper or rotating rulers to demonstrate that ray length doesn't affect angle measurement, helping students focus on the opening between the rays instead.
What Should 5th Graders Know About Lines and Angles?
By fifth grade, students should confidently identify and draw different types of angles, use a protractor to measure angles to the nearest degree, and recognize angle relationships in two-dimensional figures. They should understand that angles are measured in degrees and that a full rotation equals 360 degrees. Fifth graders also learn to calculate unknown angles using known angle measures, particularly when working with straight angles (180 degrees) and angles around a point.
This work builds directly on fourth grade geometry, where students first classified angles and identified perpendicular and parallel lines. The fifth grade focus on measurement and calculation prepares students for sixth grade work with angle relationships in triangles and other polygons. Understanding regular polygons and their angle properties in fifth grade creates a foundation for algebraic approaches to geometry in middle school.
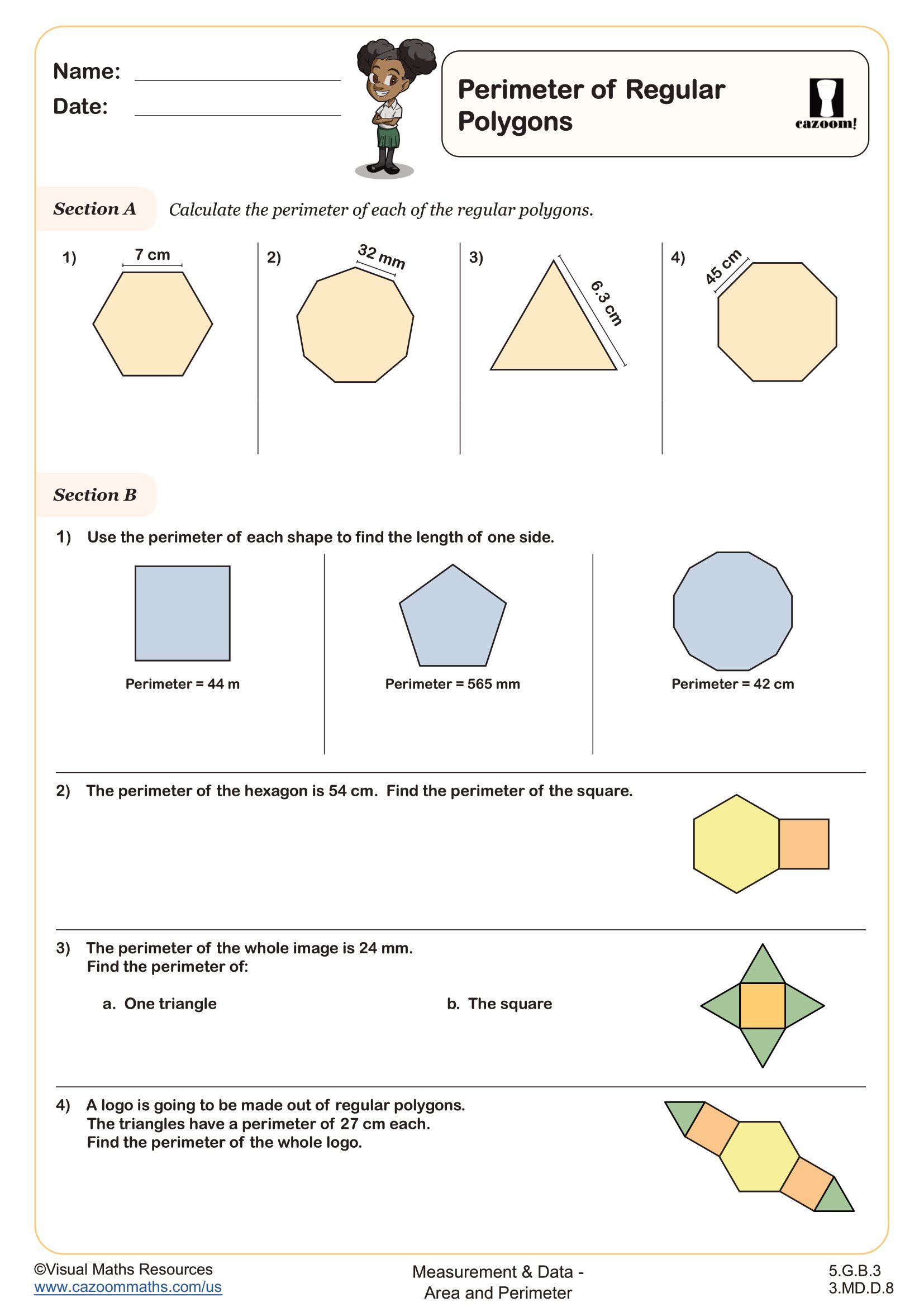
How Do Students Find the Perimeter of Regular Polygons?
Finding the perimeter of regular polygons requires students to understand that all sides have equal length. Once they know one side length and the number of sides, they multiply side length by the number of sides to find the total perimeter. For example, a regular pentagon with sides of 6 cm has a perimeter of 6 × 5 = 30 cm. This connects to their understanding of angle properties, since regular polygons also have equal interior angles.
This skill appears frequently in real-world applications, from calculating fencing needed for hexagonal garden plots to determining the border length for octagonal stop signs. Architects and engineers regularly work with regular polygons when designing structures with symmetrical properties. Students often notice the connection between perimeter formulas for regular polygons and array multiplication, recognizing that geometric problems often simplify to repeated addition or multiplication.
How Can Teachers Use These Worksheets Effectively?
The worksheets provide structured practice that moves from basic identification to application problems involving perimeter calculations. Each problem set allows students to work through examples at their own pace, building confidence before tackling more complex multi-step problems. The included answer keys let students check their work independently or allow teachers to quickly assess understanding during class.
Many teachers use these worksheets during small group instruction to target specific gaps, such as confusion about polygon properties or measurement errors. They work well as homework assignments that reinforce classroom lessons, giving students additional practice without introducing new concepts. Some teachers assign them as warm-up activities at the start of geometry units or use them for paired work, where students compare strategies for finding perimeter and discuss any differences in their approaches.