5th Grade Transformations Worksheets

These 5th grade transformations worksheets help students build spatial reasoning skills through reflections across the x and y axes on coordinate grids. Fifth graders learn to identify coordinates, apply reflection rules, and visualize how shapes move across axes while maintaining their size and properties. Teachers frequently notice that students who struggle with transformations often confuse which coordinate changes during reflection, flipping both x and y values instead of just one. This collection reinforces the connection between coordinate pairs and visual representations, preparing students for more complex geometry work in middle school. All worksheets download as PDFs with complete answer keys, making them ready for classroom practice, homework assignments, or review sessions.

Reflection in X and Y Axes

What Are Transformations in 5th Grade Math?

Transformations in 5th grade focus on moving shapes on a coordinate plane through reflections, rotations, and translations. At this level, students work primarily with reflections across the x-axis and y-axis, learning how each transformation affects the coordinates of points. Fifth graders identify the original position (pre-image) and the new position (image) after the transformation, developing understanding that reflections create mirror images across a line of reflection.

A common error occurs when students try to reflect a point across the x-axis but change both coordinates instead of just the y-coordinate. Teachers often use the memory aid "x-axis changes y" and "y-axis changes x" to help students remember which coordinate value flips while the other stays constant. This foundational work prepares students for more advanced transformations and symmetry concepts in later grades.

What Should 5th Graders Know About Transformations?

By the end of 5th grade, students should recognize and perform reflections across the x and y axes on a coordinate grid, accurately plotting both the original figure and its reflected image. The Common Core State Standards (5.G.A.1 and 5.G.A.2) expect students to graph points in the first quadrant and understand coordinate systems as preparation for transformation work. Fifth graders should also identify corresponding vertices between an original shape and its reflection, recognizing that distance from the axis of reflection remains constant.

This builds directly on 4th grade work with lines of symmetry and coordinate plotting. Students who mastered plotting ordered pairs in earlier grades transition more smoothly to understanding how transformations change coordinates systematically. These skills create the foundation for 6th and 7th grade geometry standards, where students perform transformations across all four quadrants and combine multiple transformations in sequence.

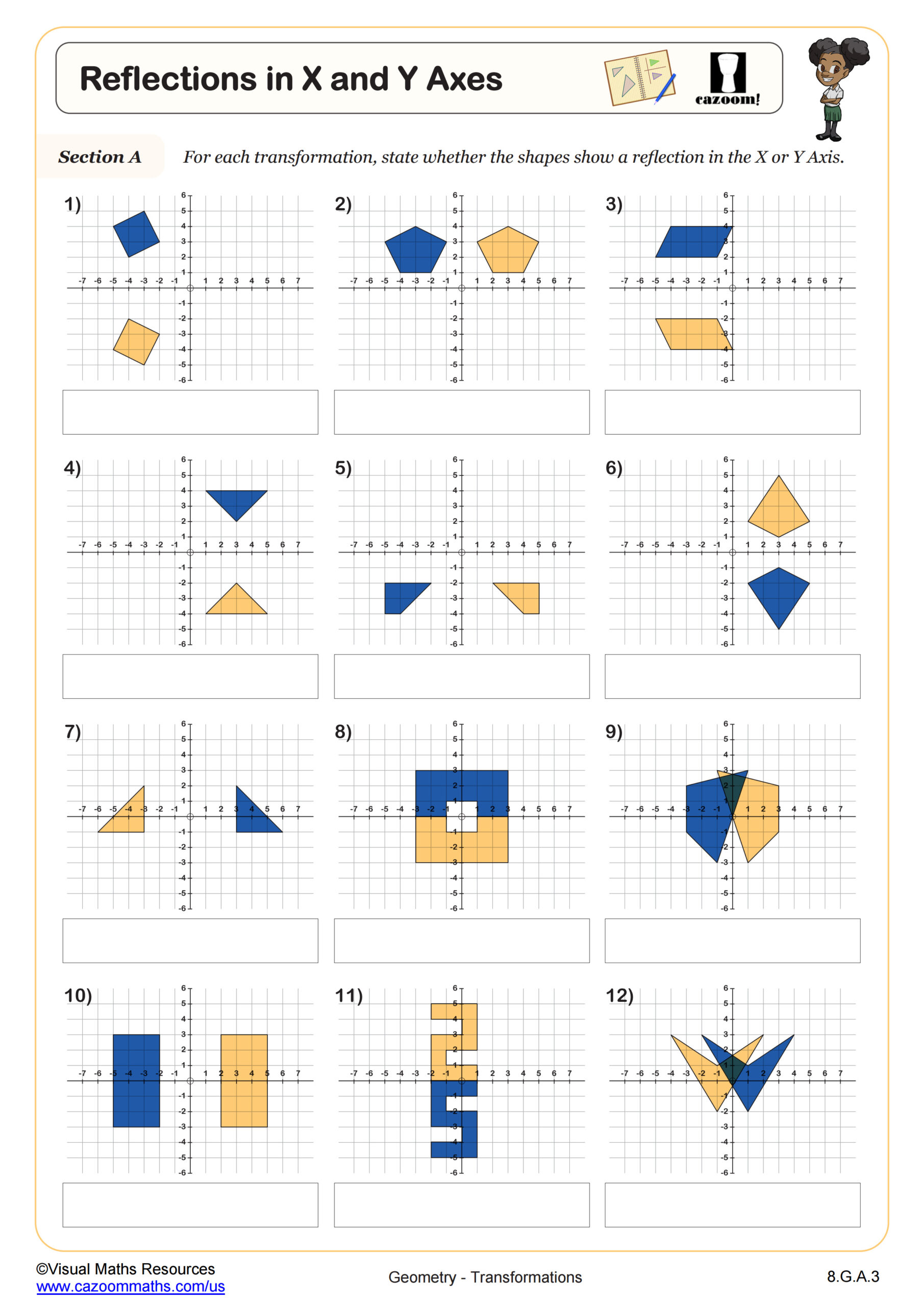
How Do Reflections Across the X-Axis and Y-Axis Work?

Reflection across the x-axis keeps the x-coordinate the same while changing the sign of the y-coordinate, transforming point (x, y) to (x, -y). Reflection across the y-axis keeps the y-coordinate constant while changing the sign of the x-coordinate, transforming point (x, y) to (-x, y). Students learn these patterns by working with multiple examples, observing that the axis of reflection acts as a mirror line and points maintain their distance from that line before and after the transformation.

Architects and graphic designers use reflections when creating symmetrical building facades and digital images. In computer animation and video game design, programmers apply transformation matrices based on these same reflection principles to flip characters and objects on screen. Understanding coordinate transformations connects to careers in engineering, robotics, and computer science, where precise spatial calculations determine how objects move and position themselves in both two-dimensional and three-dimensional spaces.

How Can Teachers Use These Transformation Worksheets?

The worksheets provide structured practice with coordinate grid reflections, allowing students to apply transformation rules systematically. Each problem requires students to identify original coordinates, apply the appropriate reflection rule, and plot the transformed image accurately. The included answer keys show complete solutions with both numerical coordinates and visual representations, helping teachers quickly identify where students make calculation or plotting errors during review sessions.

Many teachers use these worksheets during small group instruction to address specific misconceptions about which coordinate changes during reflection. The materials work well as independent practice after introducing transformations with manipulatives or dynamic geometry software. Teachers also assign these as homework to reinforce classroom learning or use them as warm-up activities to maintain skills between geometry units. Paired work allows students to check each other's coordinate calculations before plotting, catching sign errors before they affect the final graph.