5th Grade Volume and Surface Area Worksheets

Fifth grade marks students' first formal introduction to volume and surface area, building on their understanding of area from earlier grades. This collection helps students develop spatial reasoning skills as they calculate how much space a three-dimensional figure occupies and how much material covers its exterior. Teachers often notice that students initially confuse volume with surface area, trying to add all six face areas together when finding volume instead of multiplying length, width, and height. These worksheets guide students through calculating volume of rectangular prisms and cubes using the formula V = l × w × h, with clear visual representations that reinforce the connection between the formula and the physical structure. Each worksheet downloads as a PDF and includes complete answer keys for efficient grading and student self-checking.

Volume of Cubes

What Is the Difference Between Volume and Surface Area?

Volume measures the amount of space inside a three-dimensional figure, expressed in cubic units like cubic inches or cubic centimeters. Surface area measures the total area covering the outside of a solid figure, expressed in square units. Fifth graders work primarily with rectangular prisms and cubes, learning that volume answers "how much fits inside" while surface area answers "how much wraps around the outside."

Students frequently lose points on assessments when they mix up which measurement uses cubic units versus square units. A helpful classroom strategy involves using concrete examples: volume relates to filling a box with sugar cubes (counting how many fit inside), while surface area relates to wrapping that same box with paper (measuring how much paper covers all surfaces). This distinction becomes critical as students advance to middle school geometry.

What Should 5th Graders Know About Volume?

According to Common Core Standard 5.MD.C.3, fifth grade students should recognize volume as an attribute of solid figures and understand that volume is measured in cubic units. They need to measure volumes by counting unit cubes and apply the formulas V = l × w × h and V = b × h for rectangular prisms. Students should also relate volume to multiplication and addition, understanding why the formula works rather than just memorizing it.

This builds directly on fourth grade work with area formulas and multiplication fluency. Teachers notice that students who struggled with multi-digit multiplication often need extra support with volume calculations, since finding the volume of a prism with dimensions like 12 × 8 × 5 requires computational accuracy. Mastering volume in fifth grade prepares students for sixth grade work with nets, surface area formulas, and eventually volume of cylinders and pyramids in middle school.

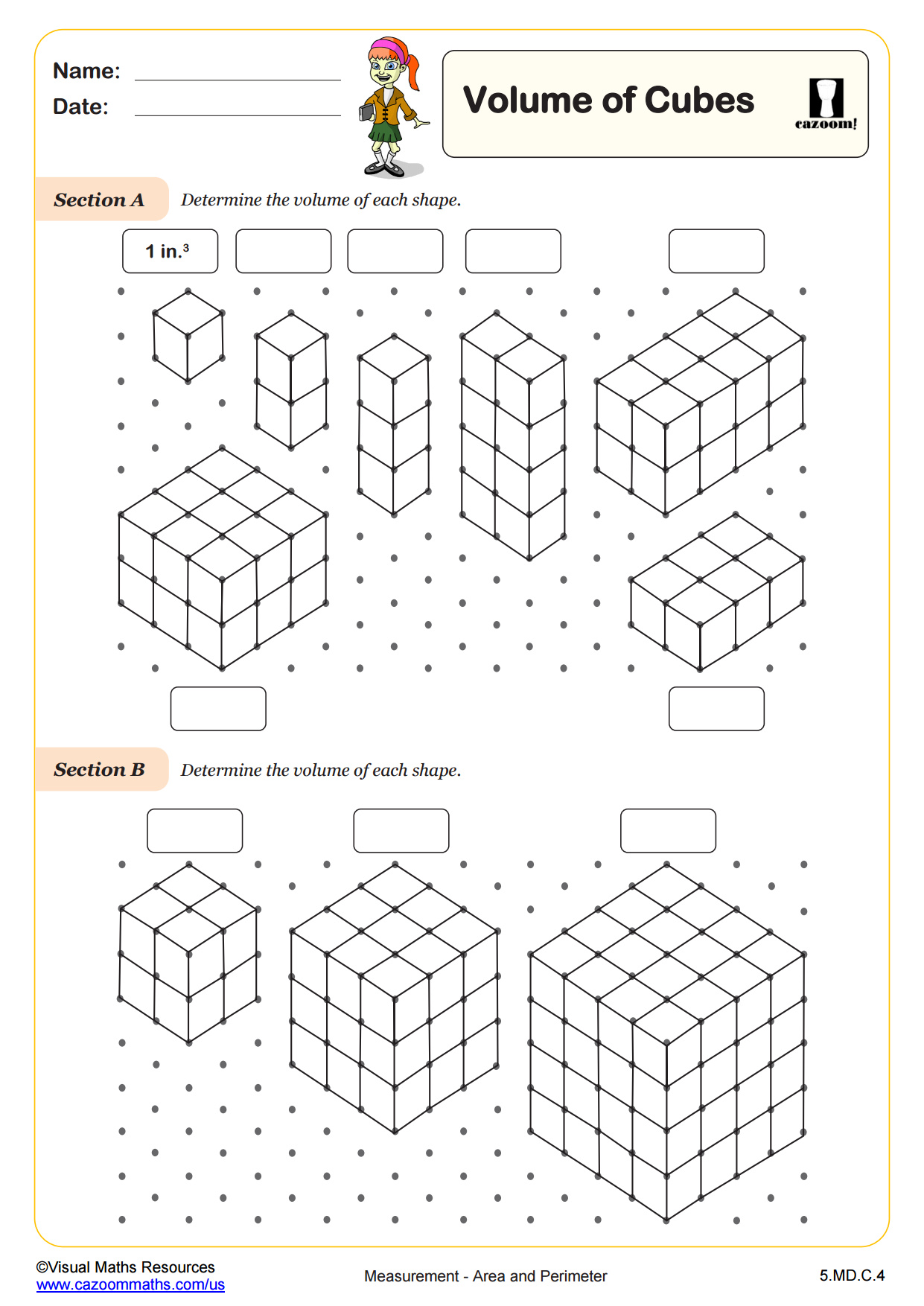
How Do You Find the Volume of a Cube?

A cube is a special rectangular prism where all edges have the same length. To find its volume, students multiply the edge length by itself three times: V = s × s × s, or V = s³. For example, a cube with 4-inch edges has a volume of 4 × 4 × 4 = 64 cubic inches. Many students recognize this as the same process they use for finding the third power of a number, making cubes an excellent bridge between geometry and exponents.

Cubes appear frequently in real-world packaging and storage contexts. Shipping companies use cubic measurements to calculate freight costs, and storage facilities advertise space in cubic feet. Students often encounter this when helping families organize moving boxes or calculating how many boxes fit in a storage unit. Understanding cube volume also connects to STEM fields like architecture, where cubic footage determines heating and cooling requirements for buildings, and manufacturing, where cubic capacity affects production planning.

How Can These Worksheets Help Students Master Volume Concepts?

The worksheets provide structured practice moving from visual cube-counting exercises to abstract formula application. Students start by counting unit cubes arranged in rectangular arrays, then transition to using dimensions and formulas. This progression helps students understand that the volume formula represents an efficient counting method rather than an arbitrary rule to memorize. Visual models showing layers of cubes help students see why multiplying length, width, and height works.

Teachers find these worksheets effective for differentiated math centers, where students working above grade level can complete problems independently while the teacher provides small-group instruction for students who need additional support. The answer keys allow for quick progress monitoring during intervention time or make the worksheets suitable for homework assignments. Many teachers use these as warm-up activities before hands-on lessons with manipulatives or as review before state assessments that include measurement and geometry standards.