6th Grade Polygons Worksheets
What Are the Key Polygon Properties Students Learn in 6th Grade?
In 6th grade, students focus on classifying polygons by the number of sides and angles, understanding that polygons are closed plane figures formed by three or more line segments. They learn to identify triangles, quadrilaterals, pentagons, hexagons, and other polygons while recognizing properties like parallel sides, perpendicular sides, and angle measures that distinguish different polygon types.
A common error occurs when students count vertices instead of sides or confuse regular polygons (equal sides and angles) with irregular polygons. Teachers often see students correctly identify a shape as a hexagon but incorrectly assume all hexagons have equal sides. Emphasizing that "regular" is a specific qualifier helps students understand that polygons can have the same number of sides while looking quite different from one another.
What Should 6th Graders Know About Polygons by the End of the Year?
By the end of 6th grade, students should confidently classify polygons based on attributes, find the area of triangles and special quadrilaterals using formulas, and work with polygons on the coordinate plane. They should understand how to break complex shapes into familiar polygons to calculate total area, a skill that appears regularly on state assessments and prepares them for composite figure problems in later grades.
This work builds directly on 5th grade experiences with coordinate grids and classifying two-dimensional figures. The polygon knowledge developed in 6th grade becomes the foundation for 7th and 8th grade work with scale drawings, cross-sections of three-dimensional figures, and eventually high school geometry topics including transformations, congruence proofs, and trigonometry. Students who master polygon properties in 6th grade find later geometry coursework significantly more manageable.
How Do Students Find the Sum of Interior Angles in Polygons?
Students learn that any polygon can be divided into triangles by drawing diagonals from one vertex, and since each triangle contains 180 degrees, they can calculate the total interior angle sum. For a polygon with n sides, the formula becomes (n-2) × 180°. A quadrilateral divides into 2 triangles (4-2=2), giving 2 × 180° = 360°, while a pentagon divides into 3 triangles, yielding 3 × 180° = 540°.
This concept connects directly to architecture and engineering, where designers must ensure angles meet correctly when creating structures. Tile designers use polygon angle properties to determine which shapes will fit together without gaps, explaining why hexagonal bathroom tiles work perfectly while regular pentagons leave spaces. Understanding interior angle sums also helps students recognize why certain polygons tessellate while others don't, a principle used in everything from flooring design to molecular chemistry structures.
How Can Teachers Use These Polygon Worksheets Most Effectively?
The worksheets provide structured practice that allows students to apply polygon concepts in engaging contexts, with the answer keys enabling students to self-check their understanding and identify errors immediately. Teachers notice that when students can verify their own work, they develop better error-analysis skills and learn to spot pattern mistakes before they become habits. The scaffolded approach helps students move from basic identification to more complex applications involving measurements and calculations.
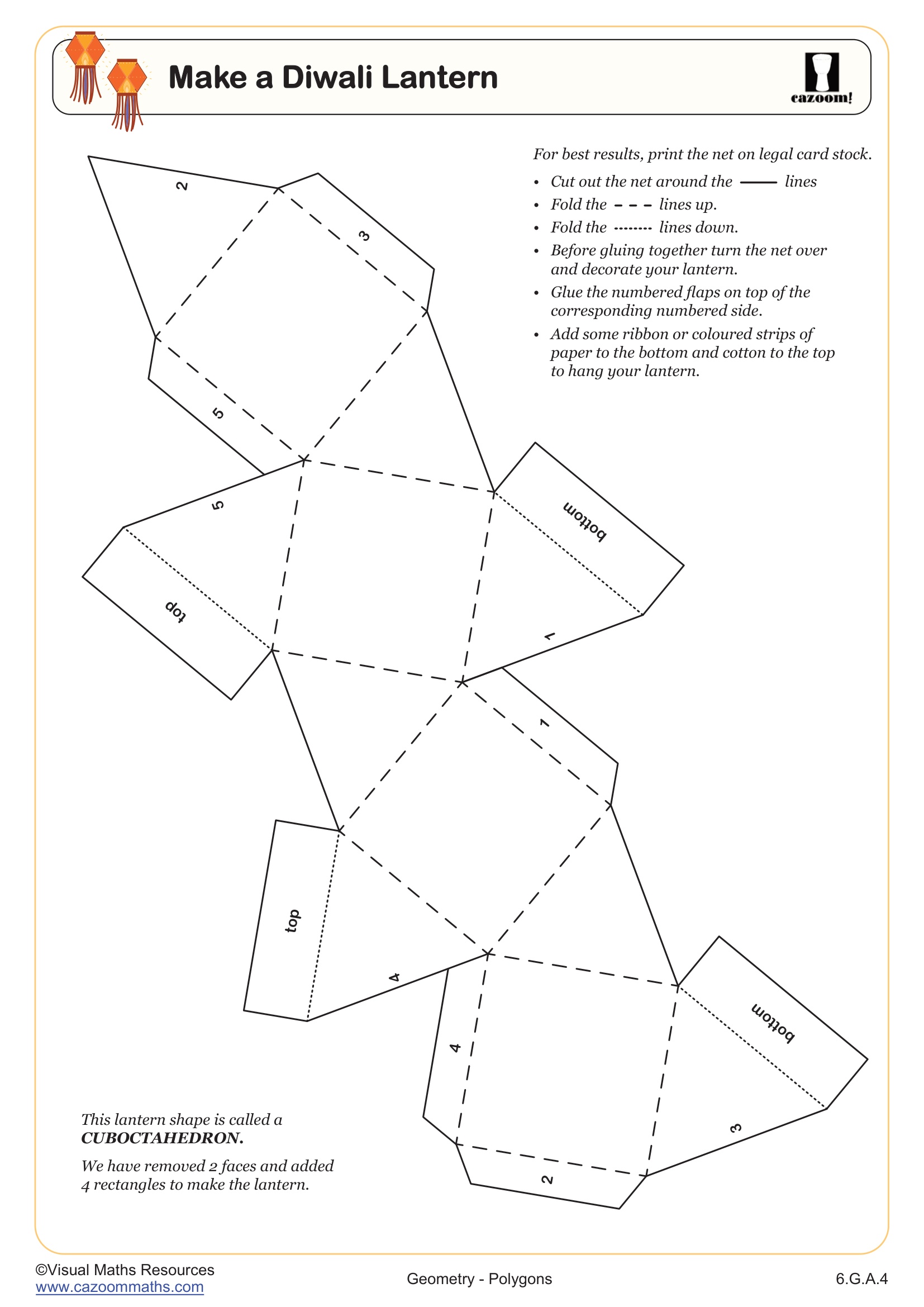
These materials work well for differentiated instruction, as teachers can assign them to students who need additional practice while working with small groups on more challenging concepts. Many teachers use polygon worksheets during math centers, as partner activities where students compare approaches, or as targeted homework following direct instruction. The cultural connection in the Diwali lantern activity also provides an opportunity to discuss how geometric principles appear across different traditions, making math feel more relevant to students' diverse backgrounds.