6th Grade Properties of Shapes Worksheets
What Are the Properties of Shapes in 6th Grade Math?
In 6th grade, properties of shapes focus primarily on understanding the characteristics of three-dimensional figures, particularly prisms and pyramids. Students work with attributes like faces, edges, vertices, surface area, and volume. The curriculum emphasizes decomposing complex shapes into simpler components, calculating measurements, and applying formulas to real geometric solids.
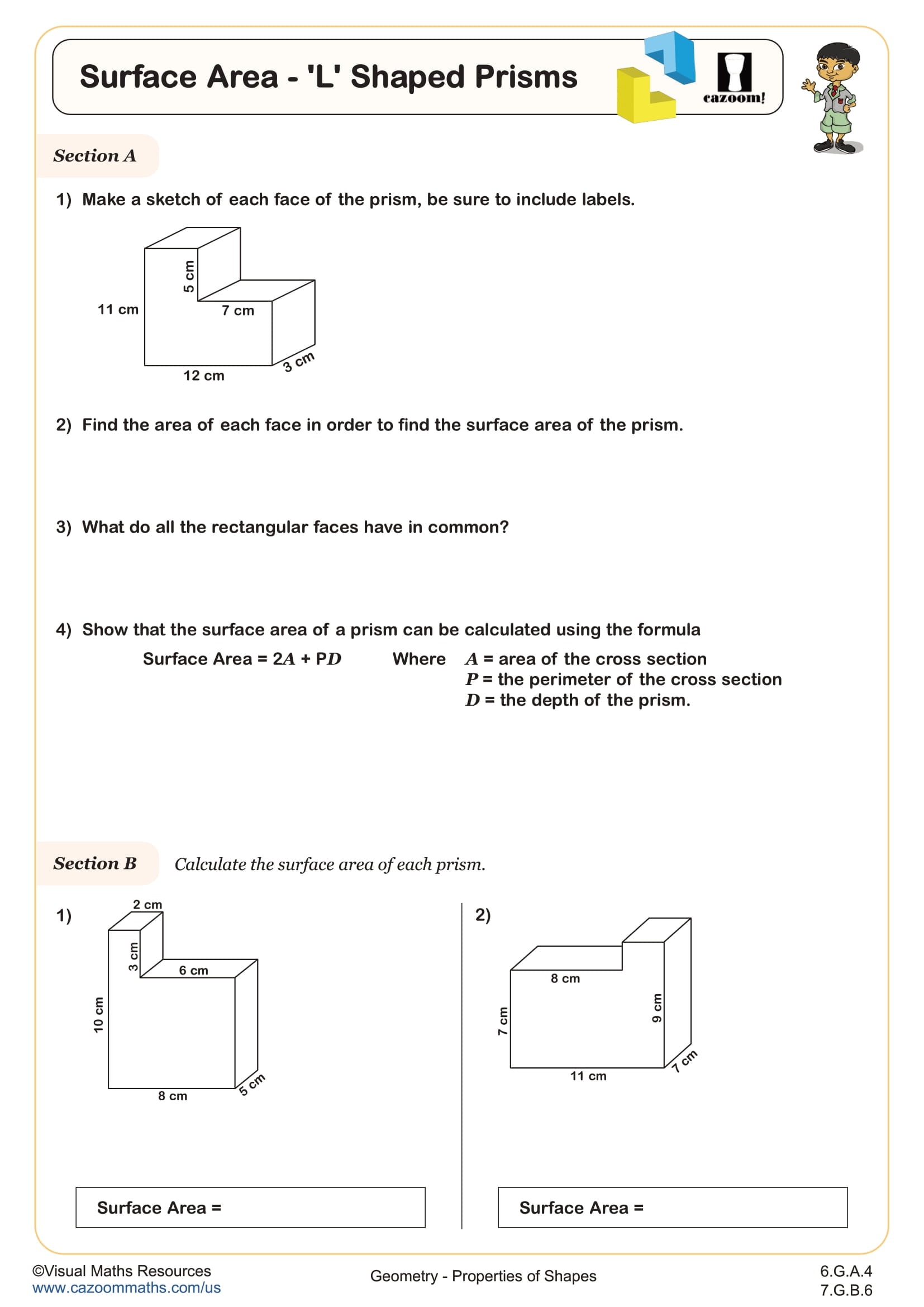
Students often lose points on assessments when they confuse surface area with volume or forget to subtract overlapping faces in composite figures. Teachers notice that success with L-shaped prisms depends on whether students can visualize the shape as two rectangular prisms joined together. This decomposition strategy becomes the foundation for finding both surface area and volume of irregular three-dimensional figures throughout middle school.
How Do 6th Graders Learn About Surface Area of Composite Prisms?
Sixth graders build on their 5th grade work with volume of rectangular prisms by adding surface area calculations and working with composite figures. Students learn to identify all faces of a three-dimensional shape, calculate the area of each rectangular face, and sum these areas while accounting for any hidden or shared surfaces. This skill aligns with Common Core Standard 6.G.A.4, which requires students to represent three-dimensional figures using nets and calculate surface area.
This topic prepares students for 7th grade geometry where they'll work with surface area and volume of cylinders, cones, and spheres. The decomposition strategy practiced with L-shaped prisms transfers directly to finding areas of composite two-dimensional figures in pre-algebra. Many state assessments include multi-step problems requiring students to both visualize composite shapes and perform accurate calculations with multi-digit numbers.
How Do You Calculate Surface Area of an L-Shaped Prism?
To find the surface area of an L-shaped prism, students mentally divide the figure into two rectangular prisms, then identify and measure all exterior faces. The key challenge involves recognizing that the interior face where the two prisms connect doesn't count toward surface area since it's hidden inside the composite shape. Students calculate the area of each visible rectangular face using length times width, then add all these areas together to find the total surface area in square units.
Architects and engineers regularly calculate surface area of composite structures when determining material quantities for construction projects. HVAC technicians need surface area calculations to estimate the ductwork required for building ventilation systems. Package designers use these same principles to minimize cardboard usage while maximizing storage space, making surface area calculations relevant across manufacturing, construction, and logistics industries. Understanding composite shapes helps students recognize how complex structures break down into manageable geometric components.
How Can Teachers Use These Surface Area Worksheets Effectively?
These worksheets provide structured practice with L-shaped prisms, helping students develop systematic approaches to decomposing composite figures. The problems guide students through identifying dimensions, counting faces correctly, and organizing calculations. Answer keys allow students to verify their decomposition strategy worked correctly and pinpoint exactly which face they may have miscounted or miscalculated, making error analysis more productive than simply marking problems wrong.
Teachers often use these worksheets during small group instruction to target students who struggled with the initial lesson or need intervention before assessments. The structured format works well for homework assignments since students can self-check using answer keys and come to class with specific questions. Some teachers assign these as warm-up problems to maintain geometry skills while teaching other units, or use them for paired work where students explain their decomposition strategies to each other, reinforcing conceptual understanding through mathematical discourse.