6th Grade Rational Numbers Worksheets
What Are Rational Numbers and Why Do Students Study Them in 6th Grade?
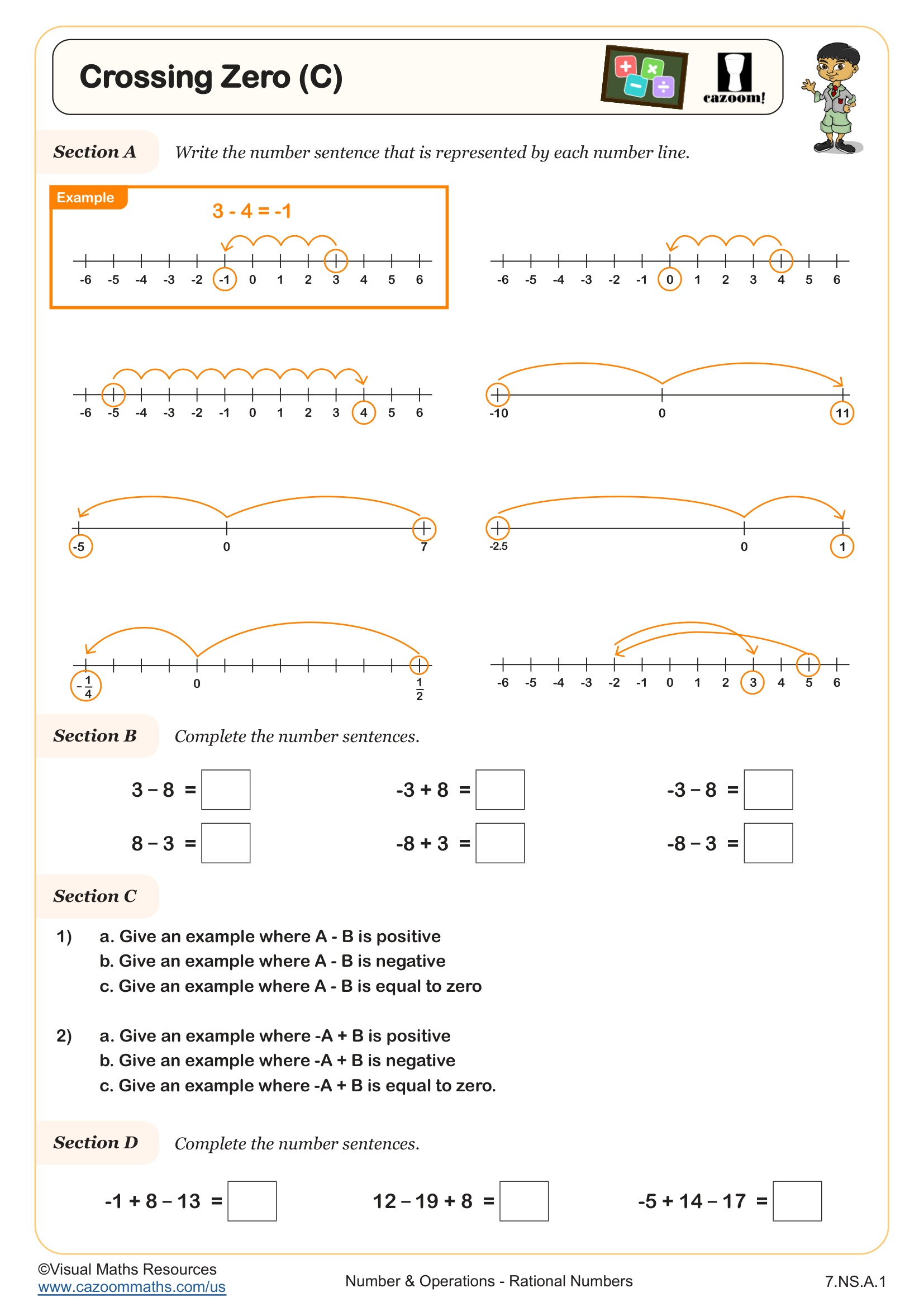
Rational numbers include any number that can be expressed as a fraction, which encompasses whole numbers, integers, decimals, and fractions themselves. In sixth grade, students extend their understanding of positive numbers to include negative values, learning that rational numbers exist on both sides of zero on a number line. This aligns with Common Core Standard 6.NS.C.6, which requires students to understand rational numbers as points on a number line and in the coordinate plane.
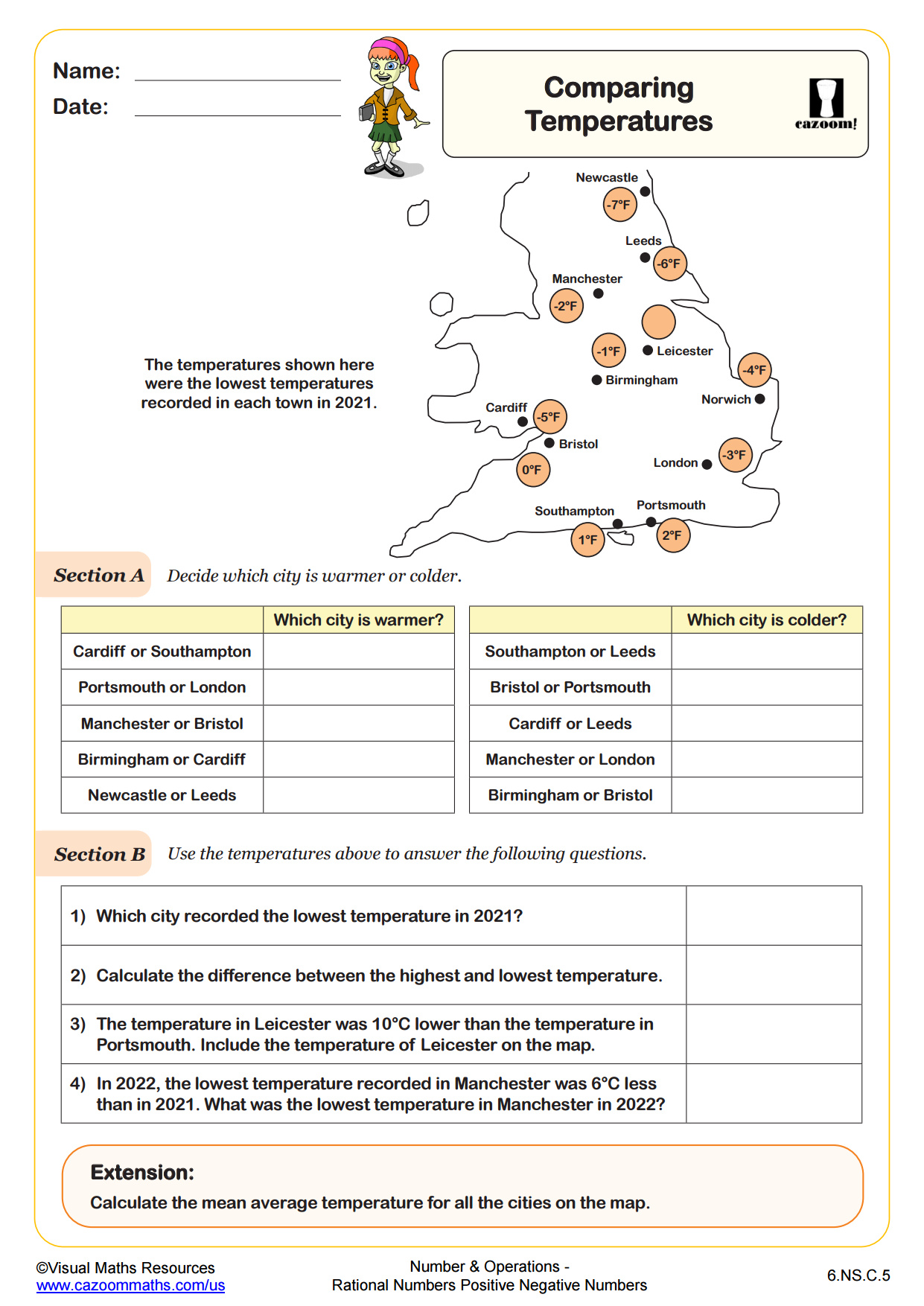
Many students make the error of thinking that negative numbers are always smaller than positive numbers in every context, leading to confusion when comparing temperatures or elevations. Teachers often use real-world scenarios like bank accounts (deposits and withdrawals) or building floors (above and below ground level) to help students recognize that "less than" depends on position relative to zero, not just the digits involved. Once students grasp that direction matters as much as magnitude, rational number concepts become significantly more accessible.
What Should 6th Graders Already Know Before Working with Rational Numbers?
By sixth grade, students should be comfortable with fraction operations, decimal place value, and understanding fractions as division. They should recognize that numbers have magnitude and be able to locate whole numbers and simple fractions on a number line. The transition to rational numbers builds directly on these skills by introducing the concept that numbers can extend in both directions from zero, creating a complete number system that includes opposites and negative values.
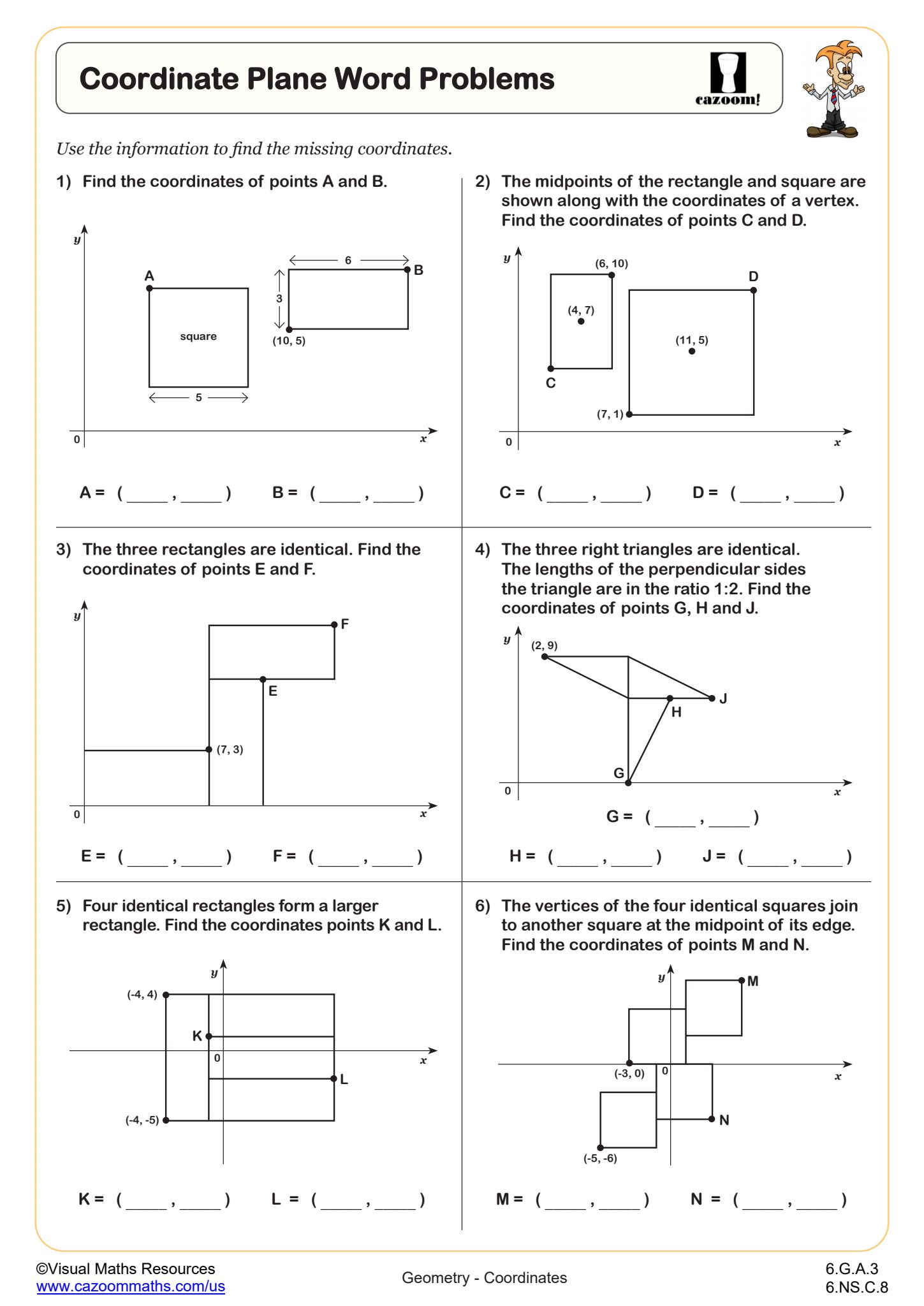
This topic prepares students for seventh and eighth grade work with operations on integers, solving equations with negative solutions, and eventually working with irrational numbers in high school geometry and algebra. Students who struggle with rational numbers often lack fluency with fraction-decimal conversions or haven't fully internalized the number line as a measurement tool. Strengthening these prerequisite skills before introducing negative values typically results in fewer misconceptions and greater confidence when graphing points in all four quadrants of the coordinate plane.
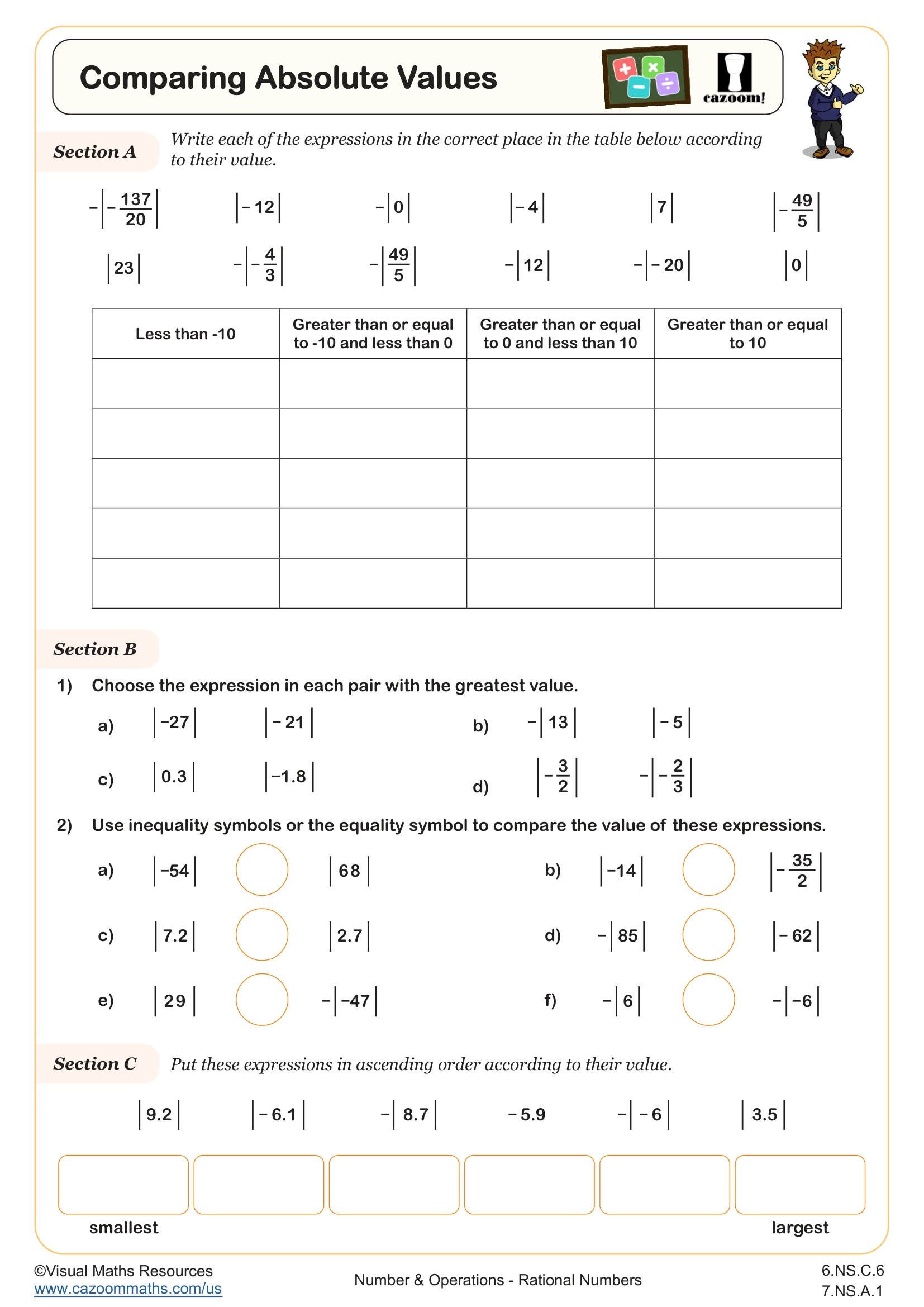
How Does Absolute Value Work and Why Is It Important?
Absolute value represents the distance a number is from zero on a number line, regardless of direction. For example, both -7 and 7 have an absolute value of 7 because each is seven units from zero. Students learn to use the notation |x| to indicate absolute value and understand that absolute value is always non-negative. This concept connects to the idea that while -5 and 5 are opposites, they share the same magnitude or size.
Absolute value appears frequently in STEM fields, particularly when calculating error margins in scientific measurements, determining temperature variations in meteorology, or measuring displacement versus distance in physics. When engineers design structures, they use absolute value to ensure materials can withstand forces from any direction. Students often experience a breakthrough when they realize that absolute value answers the question "how far?" rather than "in which direction?" This distinction becomes particularly important in middle school science classes where students measure experimental error and calculate percent difference between expected and actual results.
How Can Teachers Use These Rational Numbers Worksheets Most Effectively?
The worksheets scaffold learning by progressing from basic concepts like identifying opposites and absolute values to more complex applications involving coordinate planes and multi-step word problems. Starting with visual number line representations helps students develop intuition about rational number relationships before moving to abstract calculations. The answer keys allow teachers to quickly identify whether errors stem from conceptual misunderstandings or computational mistakes, which require different instructional responses.
Many teachers use these worksheets during guided practice after introducing new concepts, then assign similar problems for independent work once students demonstrate understanding. The coordinate plane worksheets work particularly well for partner activities, where one student plots points while another checks accuracy. Temperature comparison problems make effective warm-up exercises since they connect to students' daily experiences and naturally lead to discussions about negative numbers. Teachers also find these worksheets valuable for intervention groups, as the clear progression allows targeted practice on specific skills like distinguishing between absolute value and opposite values, which standardized tests assess separately.