6th Grade Volume and Surface Area Worksheets
What's the Difference Between Volume and Surface Area?
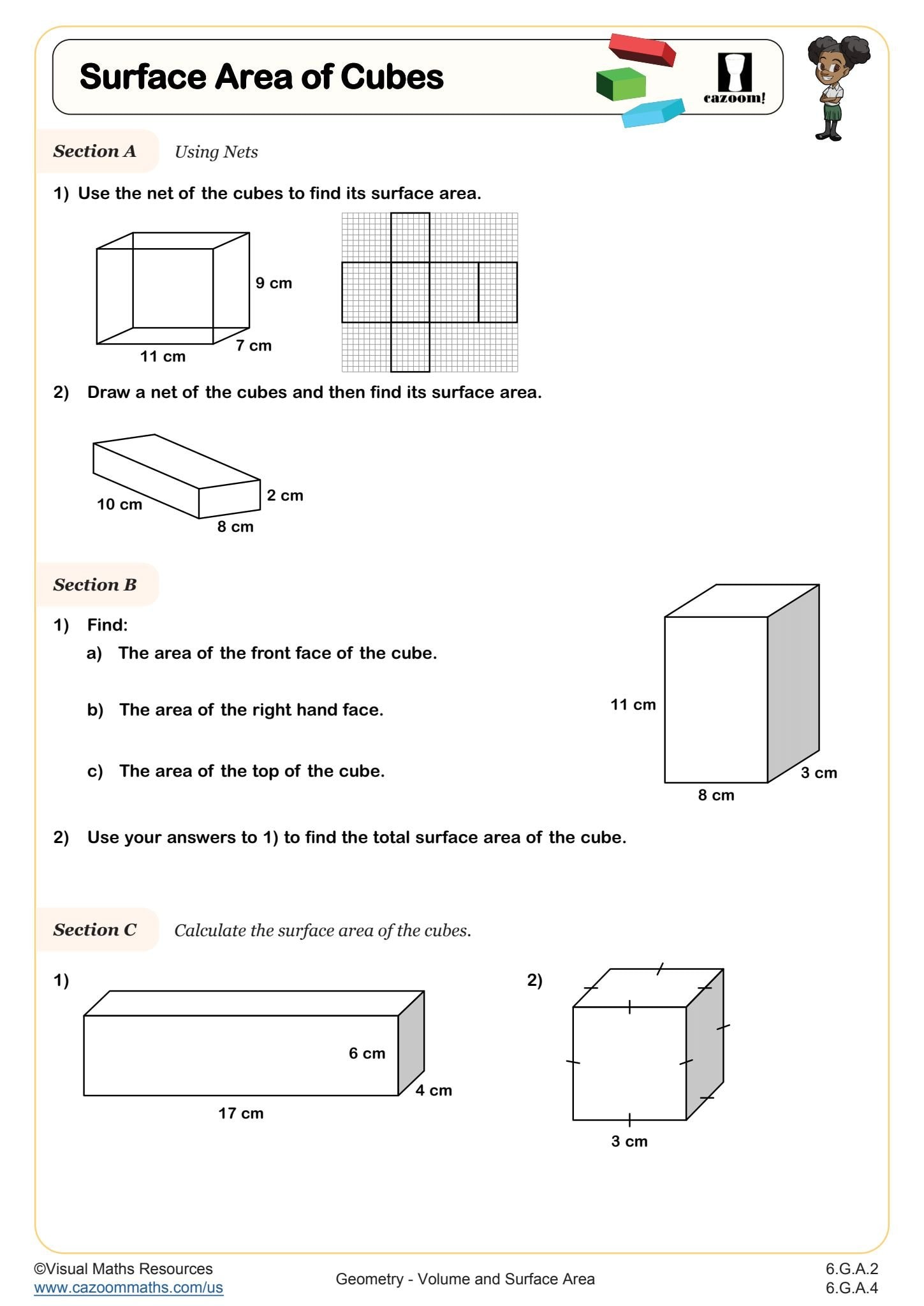
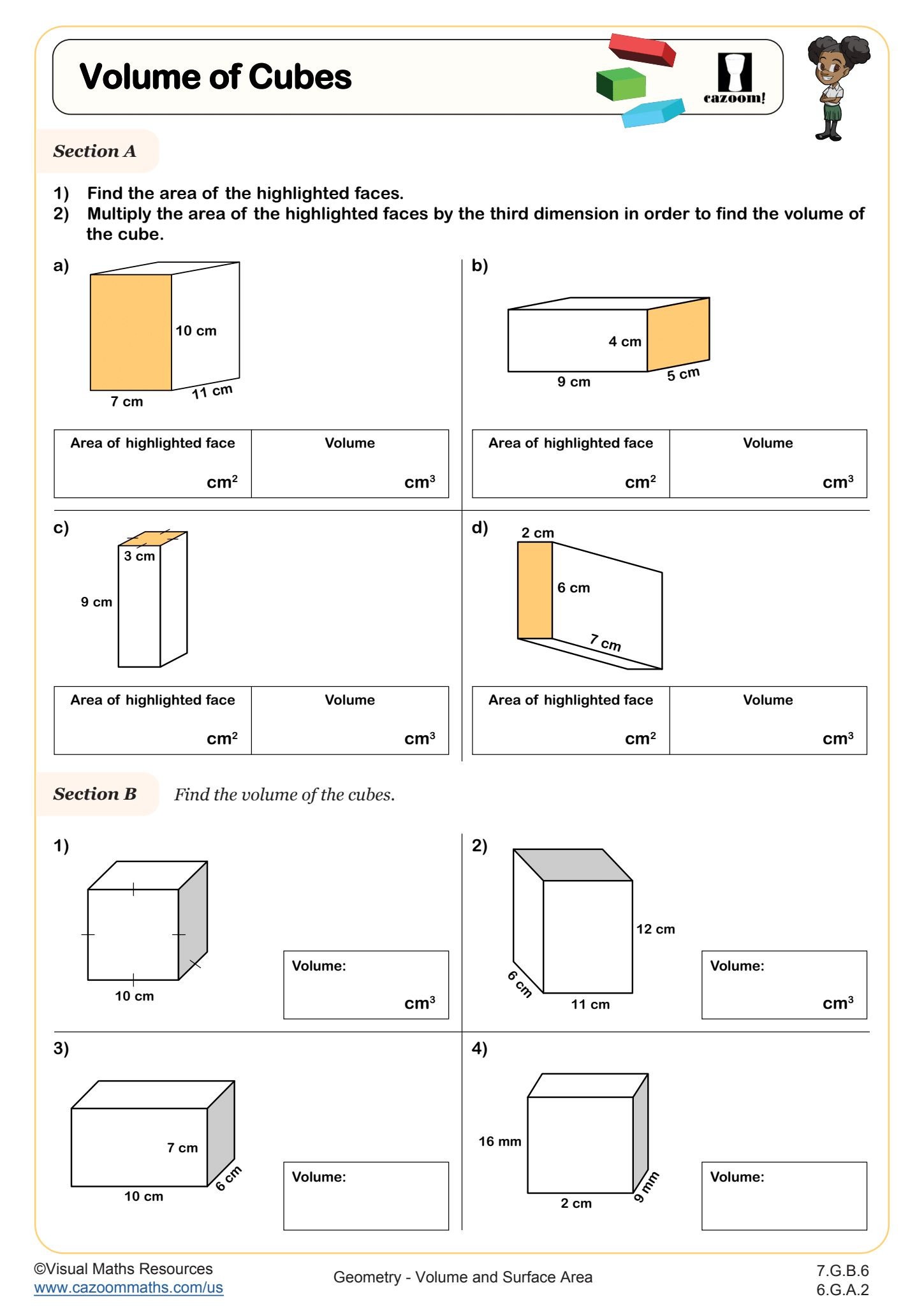
Volume measures the three-dimensional space inside a solid figure, expressed in cubic units like cubic centimeters or cubic inches. Surface area measures the total area of all outside faces of a solid figure, expressed in square units. While both concepts involve three-dimensional shapes, volume answers "how much fits inside" while surface area answers "how much material covers the outside."
Students often lose points on assessments when they mix up the units, writing cubic units for surface area or square units for volume. Teachers notice this confusion particularly when students work with cubes, where the numerical answer for surface area (6s²) and volume (s³) can be similar for certain side lengths. Emphasizing the units throughout calculation steps helps students catch their own errors before finalizing answers.
What Should 6th Graders Know About Volume and Surface Area?
According to Common Core State Standards (6.G.A.2 and 6.G.A.4), sixth graders should apply volume formulas for right rectangular prisms with fractional edge lengths and represent three-dimensional figures using nets to calculate surface area. Students work with cubes, rectangular prisms, and are introduced to pyramids, understanding that different formulas apply to different shapes. They should recognize that volume uses V = lwh for rectangular prisms and more complex formulas for pyramids.
This work builds directly on fifth grade understanding of volume with whole-number dimensions and prepares students for seventh and eighth grade study of cylinders, cones, and spheres. Teachers notice that students who master visualizing nets in sixth grade handle compound figures and composite solids much more confidently in later grades, since they've developed the habit of breaking complex shapes into manageable components.
How Do You Find the Volume of a Pyramid?
The volume of a pyramid equals one-third times the base area times the height: V = (1/3)Bh, where B represents the area of the base and h represents the perpendicular height from base to apex. Students must first calculate the base area using the appropriate formula (length times width for rectangular bases, or other area formulas for different base shapes), then multiply by the height and divide by three. A common misconception is using a slant height instead of the perpendicular height.
Pyramid volume calculations connect directly to architecture, archaeology, and engineering. The Great Pyramid of Giza required ancient Egyptians to understand these relationships when planning stone quantities for construction. Modern packaging designers use pyramid volume formulas when creating specialty containers for products, and civil engineers apply these concepts when designing drainage structures and decorative features. Students recognize that the one-third relationship means three pyramids exactly fill a prism with the same base and height.
How Can Teachers Use These Volume and Surface Area Worksheets?
The worksheets provide structured practice with progressively challenging problems, allowing students to build confidence with straightforward cube calculations before advancing to pyramids and more complex shapes. Answer keys let students check their work independently or allow teachers to quickly identify which formula applications need reinforcement. The variety across the collection means teachers can differentiate instruction by assigning specific shapes based on individual student readiness.
Many teachers use these worksheets during small-group instruction when students need focused support on distinguishing between volume and surface area formulas. They work well as homework to reinforce classroom lessons or as warm-up activities to activate prior knowledge before introducing new three-dimensional figures. Some teachers assign them as paired work, where students solve problems independently then compare solutions and reasoning, which builds mathematical communication skills alongside computational accuracy.