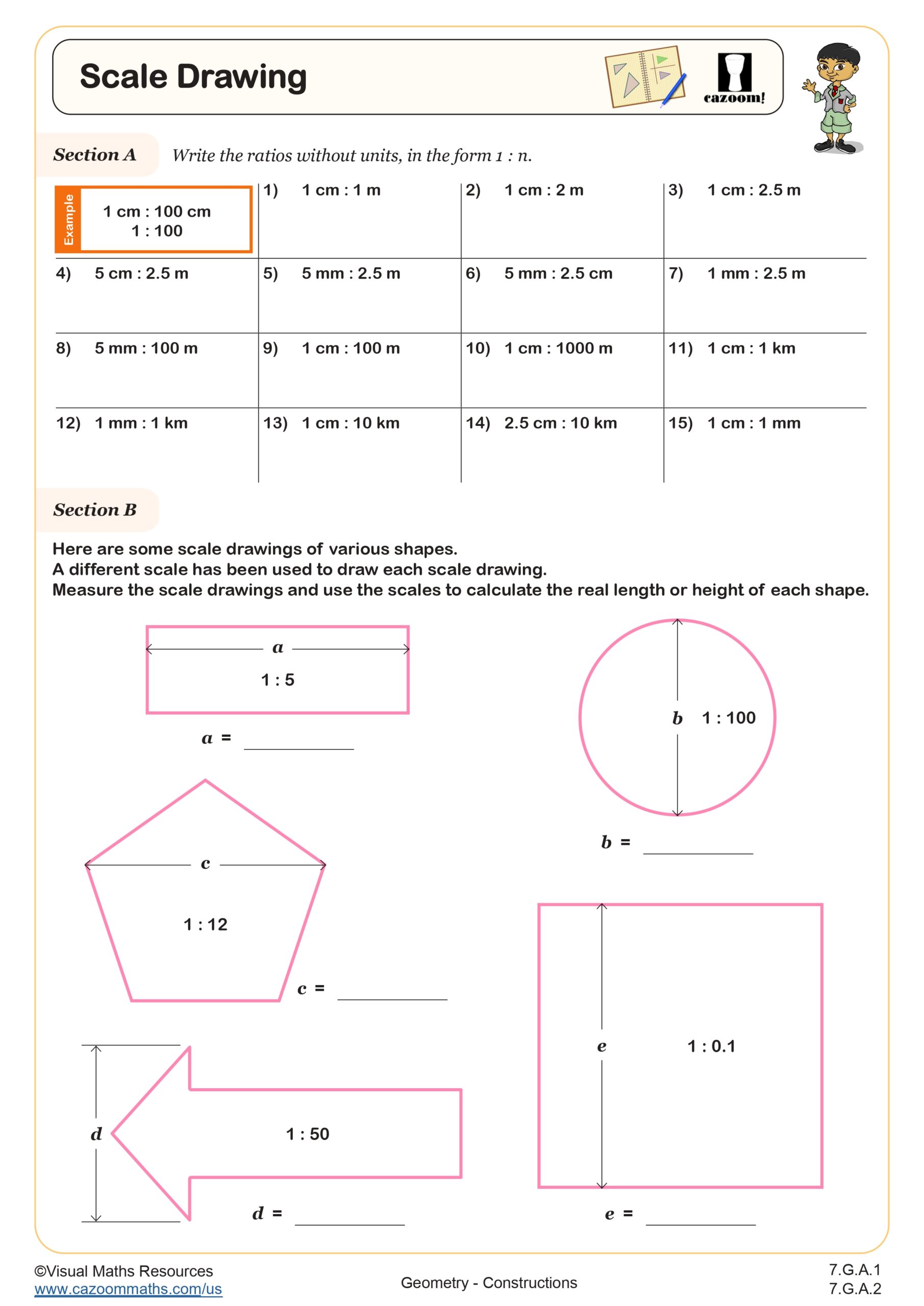
7th Grade Constructions Worksheets
What Are Geometric Constructions in 7th Grade Math?
Geometric constructions in 7th grade focus on using tools like compasses, straightedges, and rulers to create precise geometric figures and understand three-dimensional shapes through their two-dimensional representations. Students work with nets (unfolded representations of 3D shapes), construct triangles given specific measurements, explore inscribed circles, and apply angle relationships within triangles. This aligns with Common Core Standard 7.G.A.2, which requires students to draw geometric shapes with given conditions and 7.G.B.6, which addresses solving problems involving area, surface area, and volume.
A common mistake occurs when students confuse which measurements are sufficient to construct a unique triangle. Many attempt to construct triangles with combinations like three angles (which creates infinitely many similar triangles) rather than recognizing that side-side-side, side-angle-side, or angle-side-angle combinations guarantee a unique construction. Teachers often address this by having students attempt impossible constructions first, leading to the realization that not all measurement combinations work.
What Grade Level Are These Construction Worksheets For?
These worksheets are specifically designed for 7th grade students in middle school, addressing geometric construction concepts that bridge concrete geometric thinking from elementary school with the formal proof-based geometry students will encounter in high school. At this stage, students transition from simply identifying shapes to understanding the properties and relationships that define them, which prepares them for the logical reasoning required in later mathematics courses.
In 6th grade, students worked with area, surface area, and volume of basic shapes, providing the foundation for understanding nets and three-dimensional visualization. After mastering 7th grade constructions, 8th graders build on these skills by exploring transformations, congruence, and similarity, where precise construction techniques become tools for demonstrating geometric relationships. This progression ensures students develop both the technical skills and conceptual understanding needed for high school geometry.
How Do Nets and Cube Constructions Work?
Nets are two-dimensional patterns that can be folded to create three-dimensional shapes, with cube nets being particularly important because cubes have twelve edges and six faces that must connect in specific ways. Students analyze different net configurations to determine which arrangements will fold into complete cubes without overlapping faces, developing spatial reasoning skills that extend beyond simple visualization. Teachers notice that students often believe any arrangement of six squares will form a cube, but only eleven distinct net patterns actually work.
Architects and package designers rely heavily on net construction skills when creating prototypes and manufacturing specifications. Product packaging engineers use nets to minimize material waste while ensuring structural integrity, calculating how to arrange panels for the most efficient use of cardboard or other materials. Understanding nets also connects to computer graphics and 3D modeling software, where digital objects are often created by defining two-dimensional surfaces that wrap around three-dimensional frameworks, making this skill directly applicable to STEM careers in design and engineering.
How Can Teachers Use These Construction Worksheets Effectively?
The worksheets provide structured practice that builds from foundational skills to more complex applications, with answer keys allowing students to self-check their work and identify specific errors in their construction process. The mixed practice format helps students recognize which construction technique applies to different problem types, reinforcing the decision-making process that standardized assessments frequently test. Teachers find that having students explain why certain constructions are impossible (like a triangle with sides 2 cm, 3 cm, and 10 cm) deepens understanding more than simply completing successful constructions.
These worksheets work well as differentiated practice during geometry units, with struggling students benefiting from starting with the nets and faces problems before moving to triangle constructions. Many teachers assign construction worksheets as paired activities where one student reads specifications while the other constructs, then they switch roles, building communication skills alongside geometric understanding. The worksheets also serve effectively as formative assessments before state testing, helping teachers identify which construction concepts need reteaching.