7th Grade Fractions Worksheets
What fraction skills do 7th graders need to master?
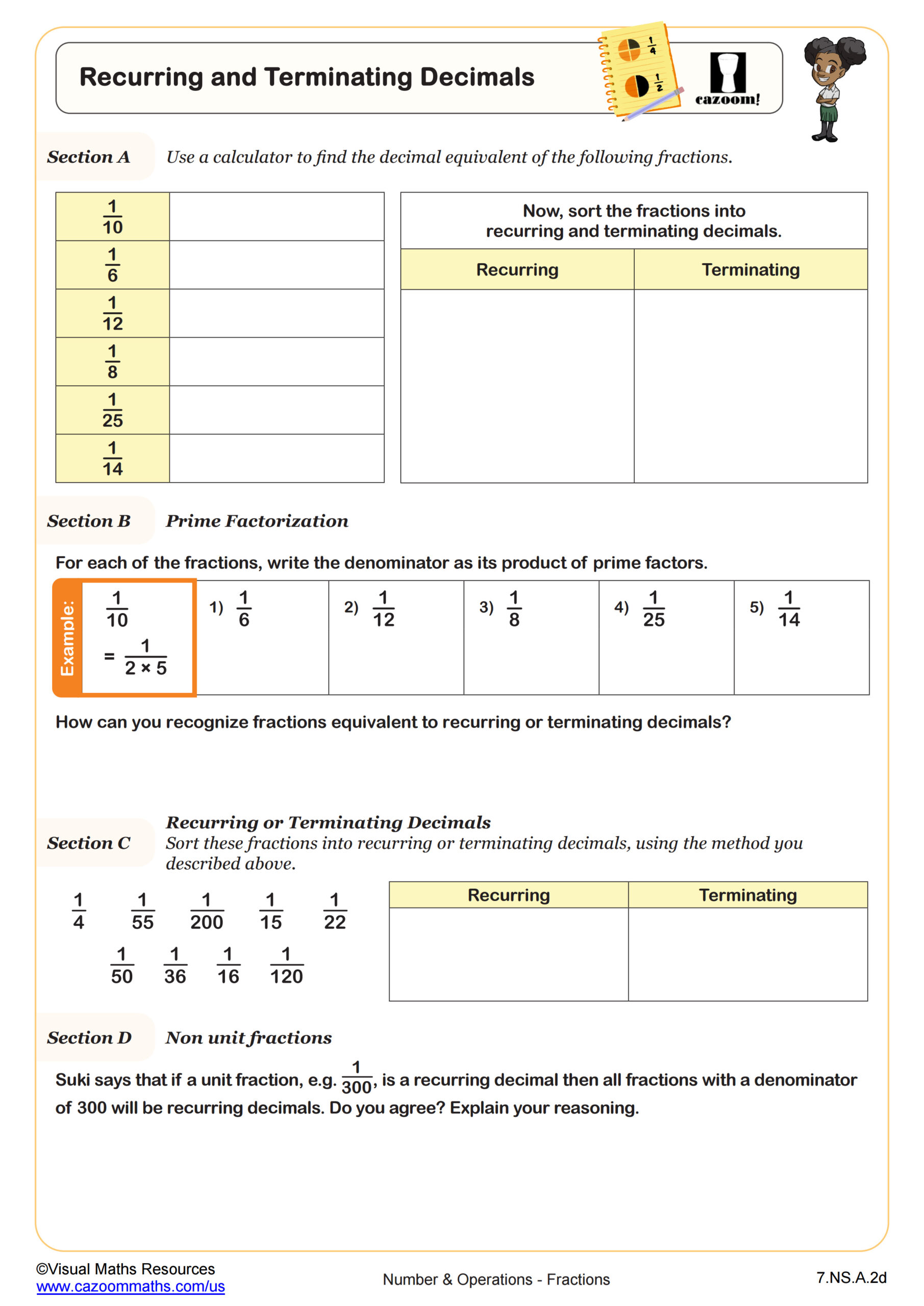
Seventh grade students work on all four operations with fractions (addition, subtraction, multiplication, and division), comparing and ordering fractions with different denominators, simplifying complex fractions, and solving problems that involve finding the whole when given a fractional part. The Common Core State Standards emphasize fluency with fraction operations by seventh grade, as students prepare for algebraic thinking and proportional relationships.
A common error occurs when students try to add or subtract fractions by adding both numerators and denominators separately, treating fractions like whole number operations. Teachers often address this by having students estimate answers first, helping them recognize that 1/2 + 1/3 cannot equal 2/5 since both fractions are nearly half, making the sum close to one whole. This estimation habit builds number sense that standardized tests reward.
Are these worksheets appropriate for middle school students?
These worksheets target 7th grade students in middle school, typically ages 12-13. At this grade level, students transition from basic fraction concepts to applying fraction operations in multi-step problems and algebraic contexts. Seventh grade sits at a critical junction where fraction fluency directly impacts success in pre-algebra and algebra courses.
In 6th grade, students focused on dividing fractions and understanding the concept of rational numbers. By 7th grade, they apply these skills to solve complex word problems and work with negative fractions. Moving into 8th grade, students use fraction operations within algebraic equations and functions, making seventh grade the year to solidify computational fluency before abstractions increase.
How do students find the whole when given a fractional part?
Finding the whole involves working backward from a fraction to determine the complete quantity. For example, if 3/5 of a number equals 15, students divide 15 by 3 to find the value of one-fifth (which is 5), then multiply by 5 to find the whole (which is 25). This skill requires understanding that fractions represent division and being comfortable with inverse operations.
This concept connects directly to real-world applications in science and engineering. When chemists prepare solutions, they often start with a concentration that represents a fraction of the final mixture and must calculate the total volume needed. Similarly, when architects scale blueprints, they work backward from fractional representations to determine actual building dimensions, making this skill foundational for STEM careers that involve proportional reasoning and measurement conversions.
How can teachers use these worksheets effectively in the classroom?
The worksheets progress from foundational skills like comparing fractions with the same denominator to more complex operations with mixed numbers and unlike denominators. This scaffolded approach allows teachers to differentiate instruction based on student readiness, assigning simpler comparison tasks to students still building confidence while challenging advanced learners with multi-step operation problems. Complete answer keys let students check their work independently, building self-assessment skills.
Many teachers use these worksheets for targeted intervention during math workshop rotations, assigning specific sheets based on assessment data that identifies which fraction skills need reinforcement. The worksheets also work well as homework assignments that parents can support using the answer keys, or as warm-up activities that review fraction concepts before introducing ratio and proportion units. Paired work allows stronger students to explain their reasoning, which deepens their own understanding.