7th Grade Measurement Worksheets
What measurement skills do 7th graders need to master?
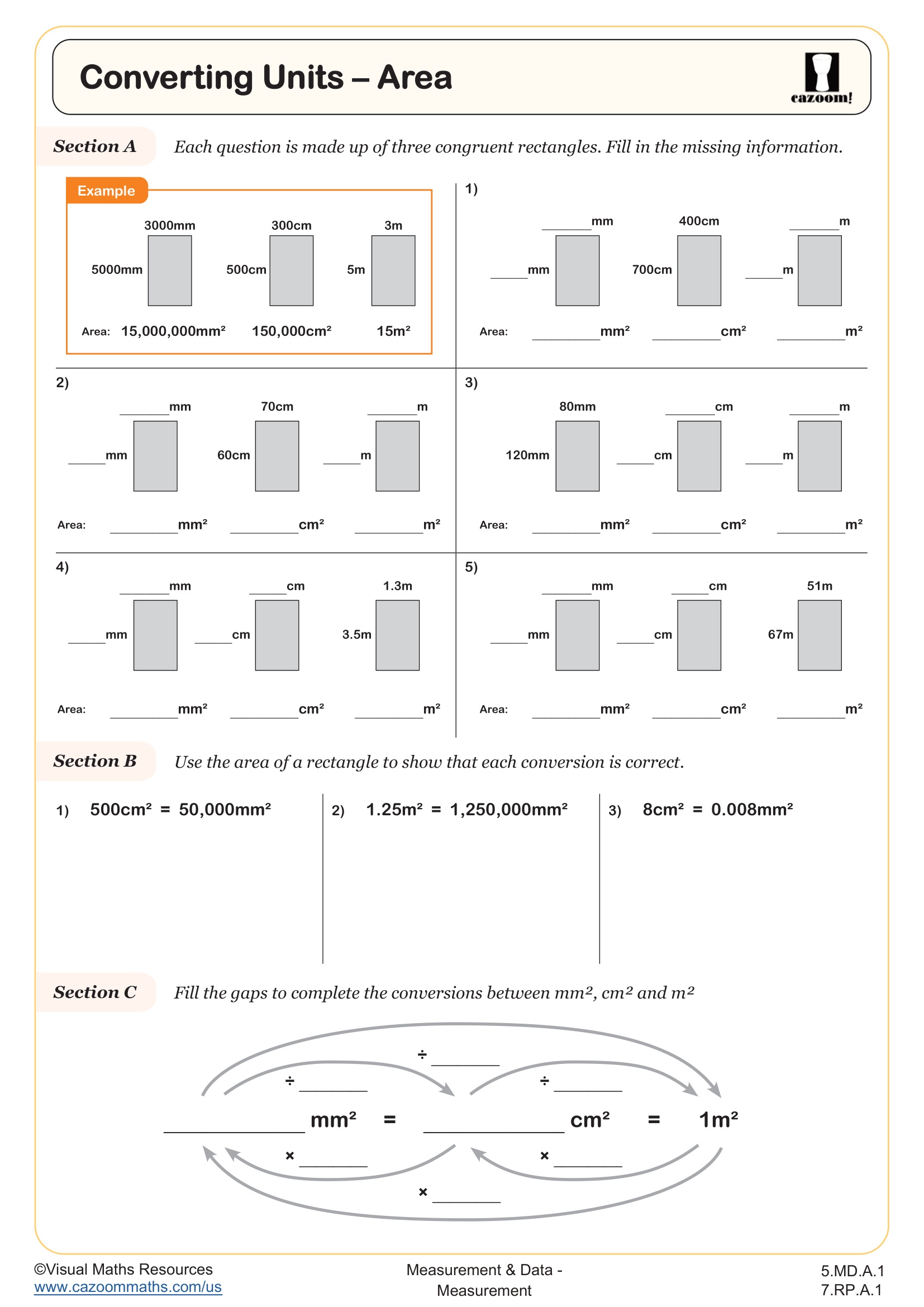
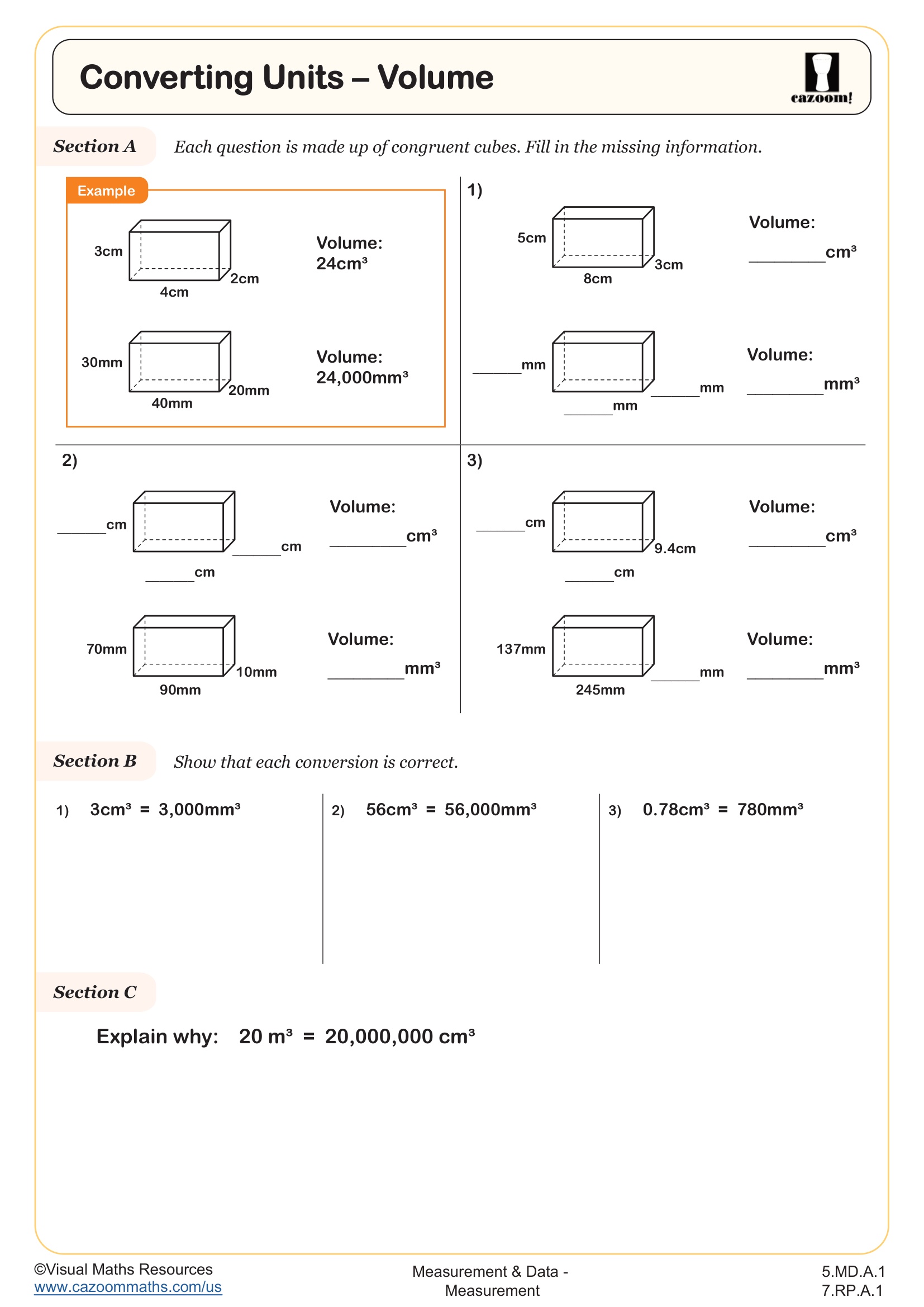
Seventh grade measurement focuses on converting within and between measurement systems, calculating area and volume of composite figures, and applying measurement concepts to solve multi-step word problems. Students work with both the customary system (inches, feet, yards, miles, ounces, pounds) and the metric system (millimeters, centimeters, meters, kilometers, grams, kilograms), converting flexibly between units. The Common Core State Standards expect students to apply proportional reasoning to these conversions and solve problems involving scale drawings and geometric measurements.
Students often struggle when conversion problems require multiple steps or switching between systems. Many lose points on assessments when they multiply instead of divide (or vice versa) during conversions, particularly when converting from smaller to larger units. Teachers notice that students gain accuracy when they learn to estimate answers first, asking themselves whether the converted value should be larger or smaller than the original measurement.
Are these measurement worksheets appropriate for middle school students?
These worksheets are specifically designed for 7th grade students in middle school, aligning with the measurement expectations for this grade level. At this stage, students transition from basic measurement concepts to more complex applications that integrate proportional reasoning, algebraic thinking, and geometric calculations. The problems require students to think critically about which operations to use and how measurements relate to each other in problem-solving contexts.
This work builds directly on 6th grade skills with ratios and unit rates, which form the foundation for conversion problems. Students who master 7th grade measurement are better prepared for 8th grade geometry, where they'll calculate surface area and volume of three-dimensional figures, and for high school physics and chemistry, where unit conversions and dimensional analysis become essential tools. The progression from concrete conversions to abstract problem-solving prepares students for STEM coursework ahead.
How do students use proportional reasoning with measurement?
Proportional reasoning in measurement means using equivalent ratios to convert between units or solve scale problems. For example, when converting 3.5 feet to inches, students set up the proportion knowing that 1 foot equals 12 inches, then solve to find 42 inches. This same reasoning applies to scale drawings, where students might use a scale of 1 inch = 4 feet to determine actual dimensions from a blueprint. Understanding that conversion factors are really unit rates helps students choose the correct operation and set up problems accurately.
This skill connects directly to careers in engineering, architecture, and healthcare, where professionals convert measurements constantly. A civil engineer designing a bridge works with blueprints at scale, converting between drawing measurements and actual construction dimensions. Pharmacists calculate medication dosages by converting between metric units based on patient weight. These real-world applications help students understand why mastering proportional reasoning with measurement matters beyond the classroom and standardized tests.
How can teachers use these measurement worksheets effectively?
The worksheets provide structured practice that moves from basic conversions to complex problem-solving, allowing teachers to differentiate instruction based on student readiness. Each problem set includes skill builders that isolate specific conversion types before combining multiple skills in word problems. The complete answer keys let teachers quickly identify patterns in student errors, whether students are struggling with the mechanics of conversion or with selecting appropriate strategies for multi-step problems.
Many teachers use these worksheets for targeted intervention with small groups who need additional practice before assessments. They work well as homework after introducing a new conversion strategy, or as warm-up activities to maintain skills throughout the year. Some teachers assign worksheets for paired work, where students compare their solution processes and catch each other's errors. The format also makes them useful for test prep, helping students recognize the types of measurement problems they'll encounter on state assessments and building the fluency they need to complete timed tests accurately.