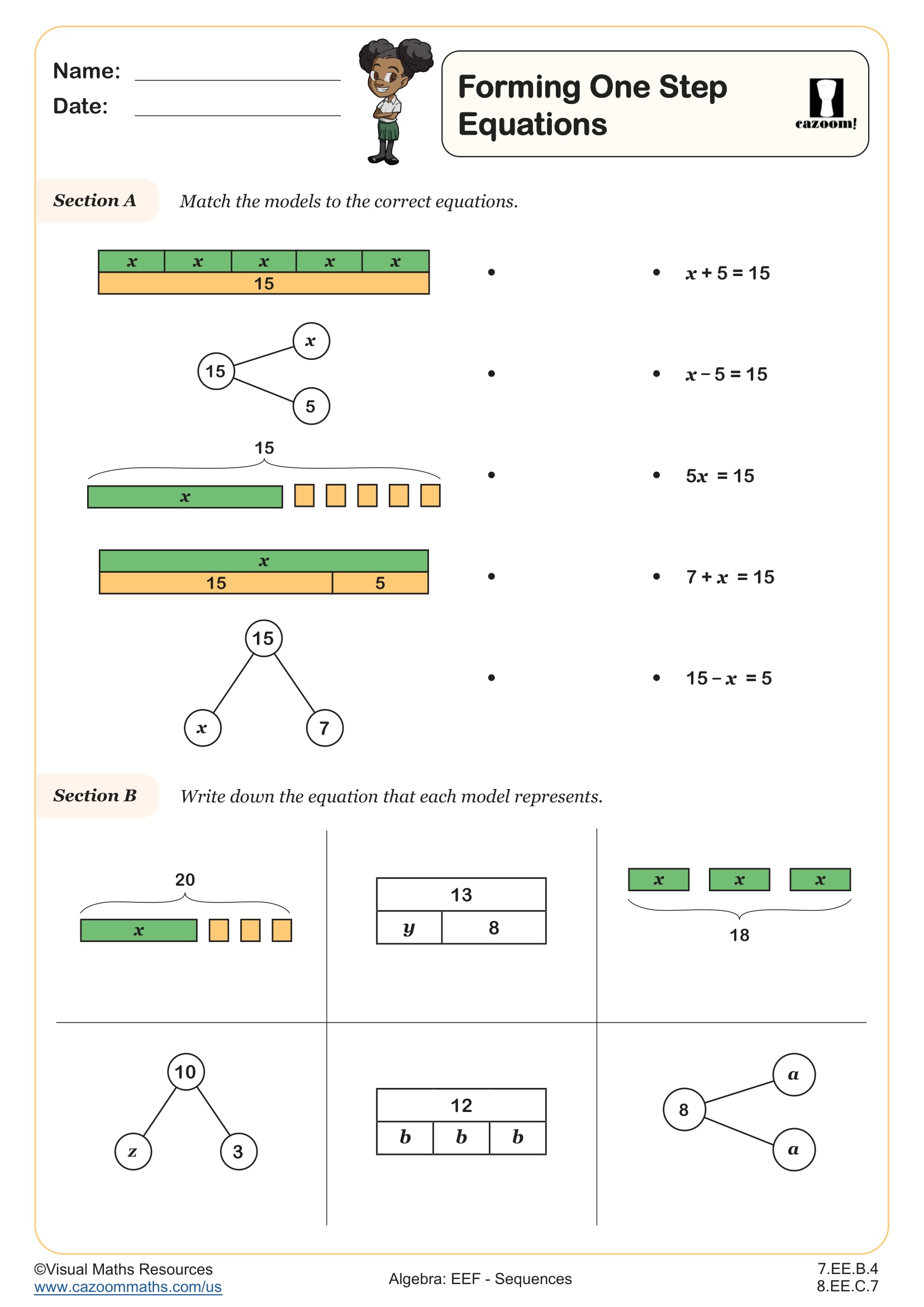
7th Grade Sequences Worksheets
What types of sequences do 7th graders learn?
Seventh grade students work with arithmetic sequences (where each term increases or decreases by a constant amount), geometric sequences (where each term is multiplied by a constant ratio), and pattern-based sequences that require visual or logical reasoning. The Common Core State Standards expect students to use variables to represent relationships in sequences and generate terms from a rule or position number.
Many students lose points on assessments because they confuse arithmetic and geometric growth—adding 3 each time versus multiplying by 3 produces very different sequences. Teachers often use visual representations or tables to help students see the distinction: arithmetic sequences show equal jumps between terms, while geometric sequences show exponential growth or decay that accelerates or shrinks dramatically.
What grade level are these sequences worksheets for?
These worksheets target 7th grade students in middle school, aligning with standards that bridge basic pattern recognition and formal algebraic reasoning. At this level, students move beyond simple number patterns from elementary school to formalize their understanding using variables, expressions, and function notation that will appear throughout algebra.
In 6th grade, students typically worked with numerical patterns and ratio tables, while 8th graders extend sequence work into linear and nonlinear functions, graphing, and exponential relationships. Seventh grade serves as the transition year where students learn to describe patterns algebraically—writing expressions like 3n + 2 for the nth term rather than just continuing a pattern by observation.
How do arithmetic sequences connect to real-world situations?
Arithmetic sequences model any situation with constant change over equal time intervals. Students learn to write nth term formulas in the form a + (n - 1)d, where a represents the starting value and d represents the common difference between consecutive terms. This algebraic representation transforms pattern observation into a predictive tool.
Students encounter arithmetic sequences when calculating savings plans (depositing $20 weekly), construction projects (stacking blocks in rows that decrease by 2 each level), or subscription costs with flat monthly fees. In STEM fields, arithmetic sequences appear in computer science algorithms, engineering designs with uniform spacing, and scientific data showing linear growth rates. Students confidently tackle word problems once they recognize the constant difference signals an arithmetic sequence and translate the context into algebraic notation.
How can teachers use these sequence worksheets in the classroom?
The worksheets scaffold learning by starting with visual patterns and continuing sequences before progressing to generating terms from nth term rules and working backward to find formulas. Answer keys allow students to check their work independently during practice, helping them catch errors in pattern recognition or calculation before those mistakes become habits.
Teachers use these worksheets for targeted intervention when students struggle with specific sequence types, as warm-up activities to activate prior knowledge before introducing functions, or as homework that reinforces classroom instruction. Paired work helps students articulate their reasoning—explaining why a sequence is arithmetic versus geometric often solidifies understanding better than silent practice. The variety of subtopics allows teachers to differentiate, assigning geometric sequences to students ready for challenge while others master arithmetic sequences first.