7th Grade Units and Dimensions Worksheets
What Are Units and Dimensions in 7th Grade Math?
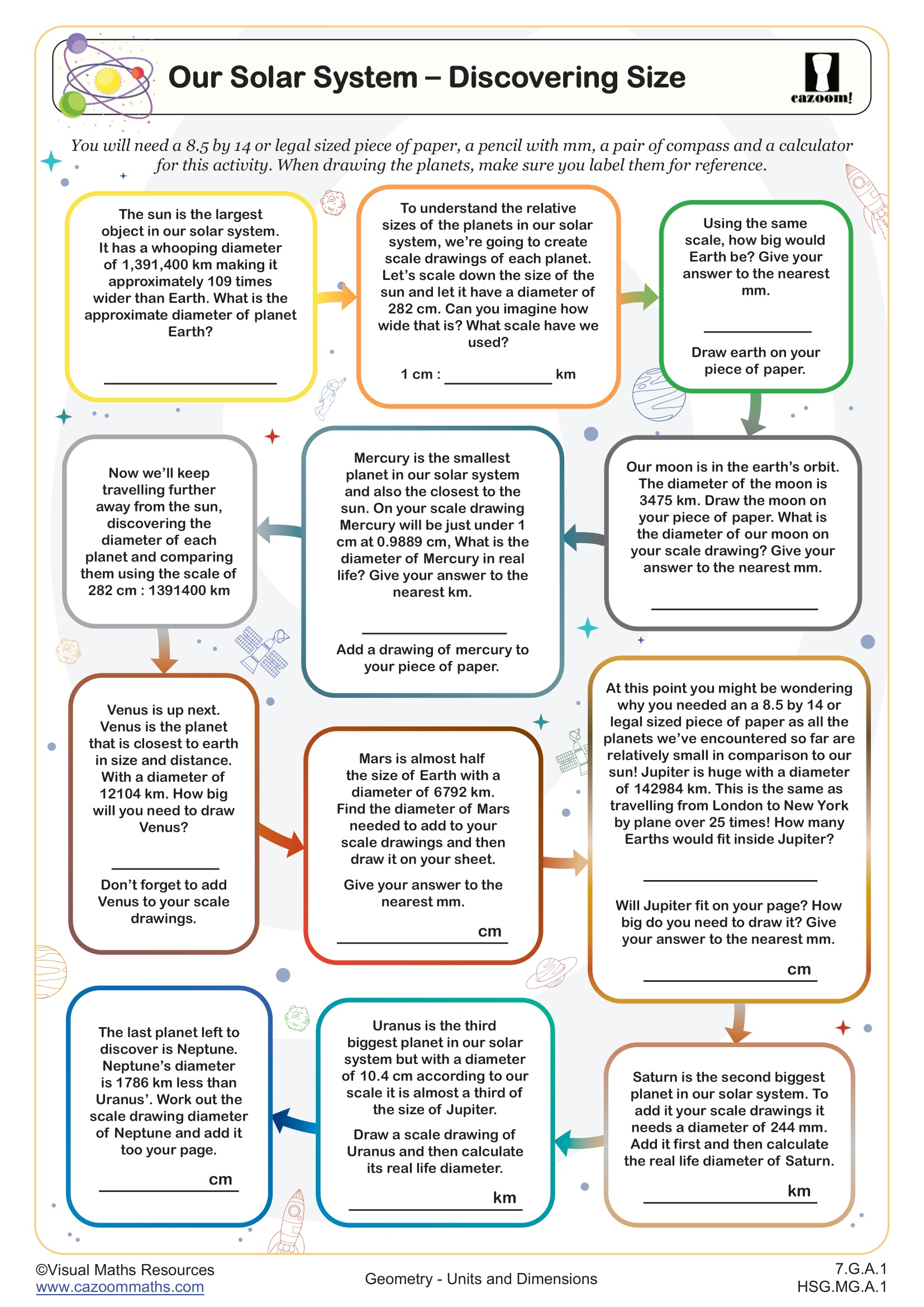
Units and dimensions in 7th grade mathematics encompass measurement conversions within the metric system and understanding how dimensions relate to geometric formulas. Students work with linear units like meters, centimeters, and millimeters, mass units including grams and kilograms, and learn to identify whether formulas calculate one-dimensional perimeter, two-dimensional area, or three-dimensional volume. This aligns with Common Core standards 7.G.A.1 and 7.G.B.6, which address solving real-world problems involving area, surface area, and volume.
Many students initially struggle to distinguish when a problem requires area versus perimeter or volume, often selecting formulas based on familiarity rather than dimensional analysis. Teachers frequently observe that breakthrough happens when students recognize patterns in units: perimeter yields linear units (cm), area produces square units (cm²), and volume results in cubic units (cm³). This dimensional awareness prevents the common error of calculating area when the problem context clearly requires perimeter, or vice versa.
What Grade Level Are These Units and Dimensions Worksheets For?
These worksheets are specifically designed for 7th grade students in middle school, typically ages 12-13. At this stage, students refine measurement skills developed in earlier grades and apply them to increasingly complex geometric contexts. Seventh grade represents the transition from basic measurement operations to analytical thinking about how dimensions behave in formulas and real-world applications.
In 6th grade, students learned fundamental metric conversions and calculated area and volume of basic shapes. Eighth grade builds on 7th grade units and dimensions work by introducing the Pythagorean theorem, volumes of cylinders and spheres, and scientific notation involving units. The 7th grade curriculum serves as the bridge, ensuring students can fluently convert measurements and match formulas to contexts before tackling more abstract applications. Students who master dimensional reasoning in 7th grade find 8th grade geometry significantly more accessible.
How Do Students Work with Nets and Faces of Cubes?
Working with nets and faces of cubes develops spatial reasoning by asking students to visualize how two-dimensional patterns fold into three-dimensional shapes. Students identify which flat patterns (nets) can fold to form a cube and count faces, edges, and vertices. This skill requires mental rotation and the understanding that a cube has six congruent square faces, twelve edges, and eight vertices, regardless of how the net is arranged.
This visualization skill connects directly to STEM fields, particularly engineering and architecture, where professionals must read two-dimensional blueprints and translate them into three-dimensional structures. Packaging designers use net patterns to create efficient box designs that minimize material waste while maximizing structural integrity. Students often make the connection between cube nets and the flat cardboard patterns they see before boxes are assembled, helping them recognize that mathematical concepts govern everyday manufacturing and design processes.
How Can Teachers Use These Units and Dimensions Worksheets?
The worksheets provide structured practice that scaffolds from basic unit conversions to formula matching and three-dimensional reasoning. Each problem set progresses in complexity, allowing students to build confidence with straightforward conversions before applying that knowledge to geometric contexts. The included answer keys enable students to check their work independently, promoting self-correction and metacognitive skills as they identify where errors occurred in their conversion process or formula selection.
Teachers use these worksheets effectively for targeted intervention with students who struggle on state assessments requiring measurement skills, as warm-up activities to activate prior knowledge before geometry units, or as homework that reinforces classroom instruction. They work particularly well in paired activities where students compare their formula matching reasoning or check each other's conversion calculations. The mix of conversion practice and geometric application makes the collection suitable for differentiation, allowing teachers to assign specific sections based on individual student needs identified through formative assessment.