8th Grade Estimation Worksheets
Why is estimation important in 8th grade math?
Estimation serves as a critical check for reasonableness in 8th grade, especially as students use calculators more frequently and work with irrational numbers. The Common Core State Standards emphasize estimation as a tool for validating computational results and developing mental math fluency that supports algebraic thinking and problem-solving across all mathematical domains.
Students lose points on standardized assessments when they accept unreasonable calculator outputs without questioning them. For example, when finding the square root of 50, students who don't estimate between 7 and 8 might accept 25 or 2500 as reasonable answers. Teachers frequently notice that students who practice estimation catch their own errors before submitting work, demonstrating stronger metacognitive skills that extend beyond mathematics.
What estimation skills should 8th graders master?
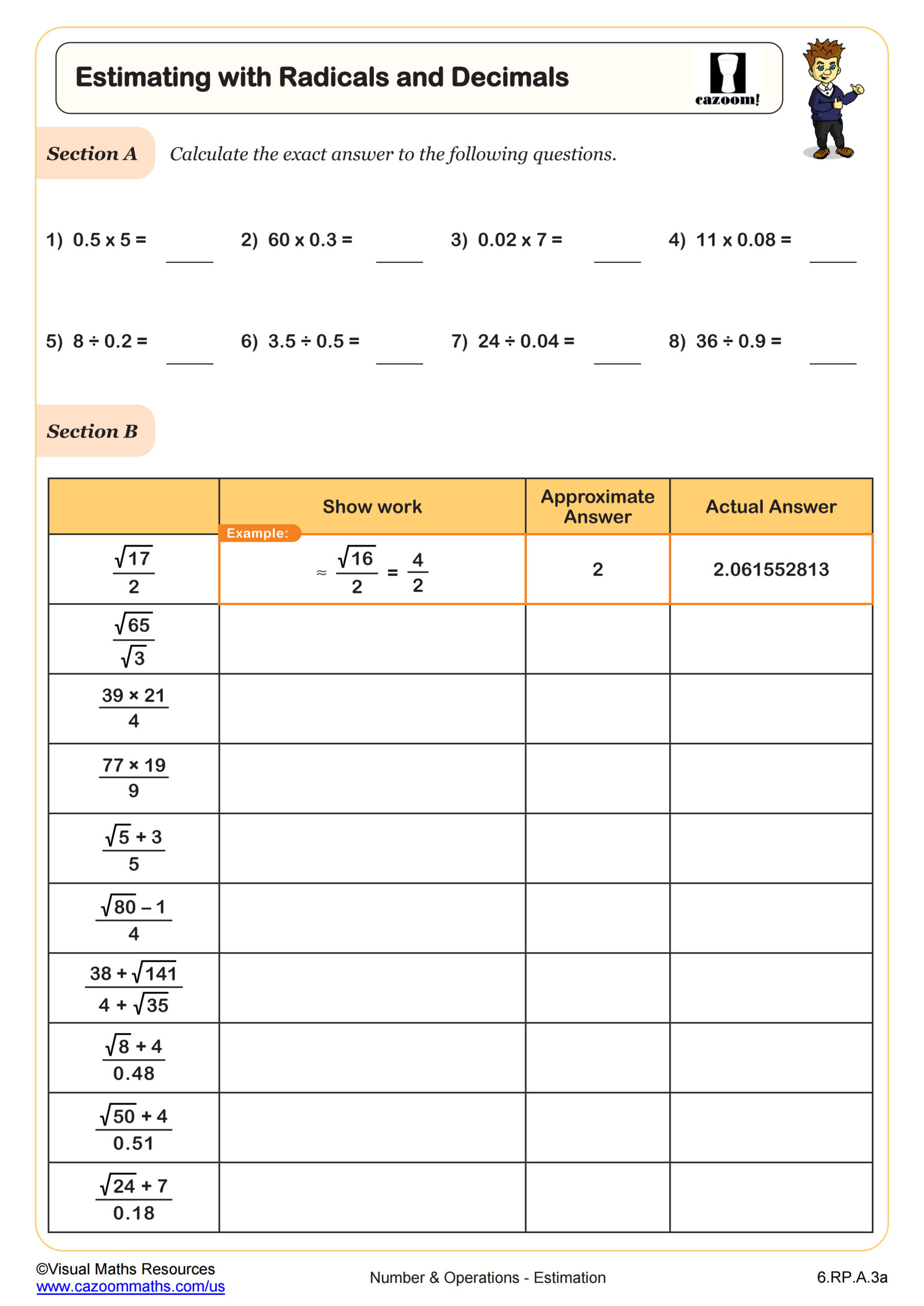
By 8th grade, students should estimate square roots of non-perfect squares by identifying the nearest perfect squares, approximate operations with radicals, and round decimals strategically based on context. They need to work comfortably with benchmark fractions and their decimal equivalents, understanding when to round up versus down depending on the real-world situation. This skill set directly supports their work with the Pythagorean theorem, scientific notation, and rational versus irrational number classification.
These estimation abilities build on the place value understanding and rounding strategies from elementary school while preparing students for high school algebra and geometry. Students who master estimation in 8th grade approach functions, exponential growth, and trigonometry with stronger intuition about expected answer ranges, making them less dependent on technology for validation.
How do students estimate square roots effectively?
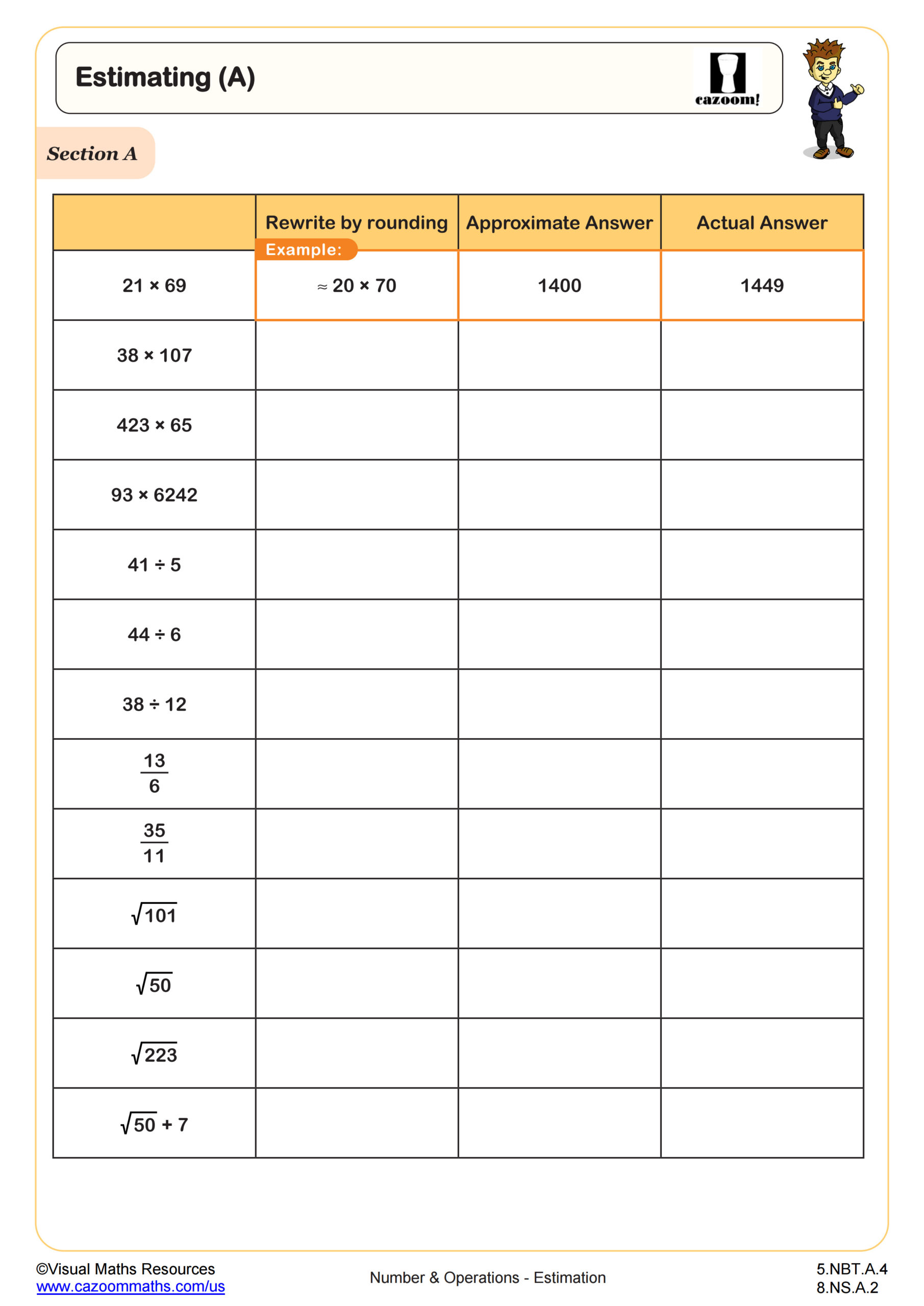
Estimating square roots requires students to identify the two consecutive perfect squares that bracket the number, then determine which is closer. For example, to estimate √73, students recognize that 64 < 73 < 81, so √73 falls between 8 and 9. Since 73 is closer to 81 than to 64, the estimate should be closer to 9, perhaps around 8.5 or 8.6. Many students make the connection between this process and their earlier work with number lines, using proportional reasoning to refine their estimates.
This skill appears regularly in STEM fields, particularly in physics and engineering where calculations involve dimensions and measurements. Construction professionals estimate square roots when determining diagonal measurements, while data scientists approximate standard deviations without reaching for calculators. Students confidently tackle more complex radical expressions once they recognize that estimation provides a mental framework for evaluating their algebraic manipulations.
How should teachers use these estimation worksheets?
These worksheets provide structured practice that progresses from straightforward square root estimation to more complex scenarios involving radicals and decimal operations. The answer keys allow students to self-check their work, encouraging them to analyze which estimation strategies yield the most accurate results. Teachers often use the worksheets to diagnose whether students understand perfect squares and benchmark values before moving into more abstract algebraic concepts.
The worksheets work well as warm-up activities to activate number sense before calculator-intensive lessons, or as intervention resources for students who struggle with reasonableness checks. Many teachers assign them as homework following lessons on irrational numbers or radical operations, then use paired work to have students explain their estimation strategies to each other. They're also effective during test review sessions, helping students develop the mental math habits that prevent careless errors on assessments.