Algebra I Indices Worksheets
What Do Algebra I Indices Worksheets Cover?
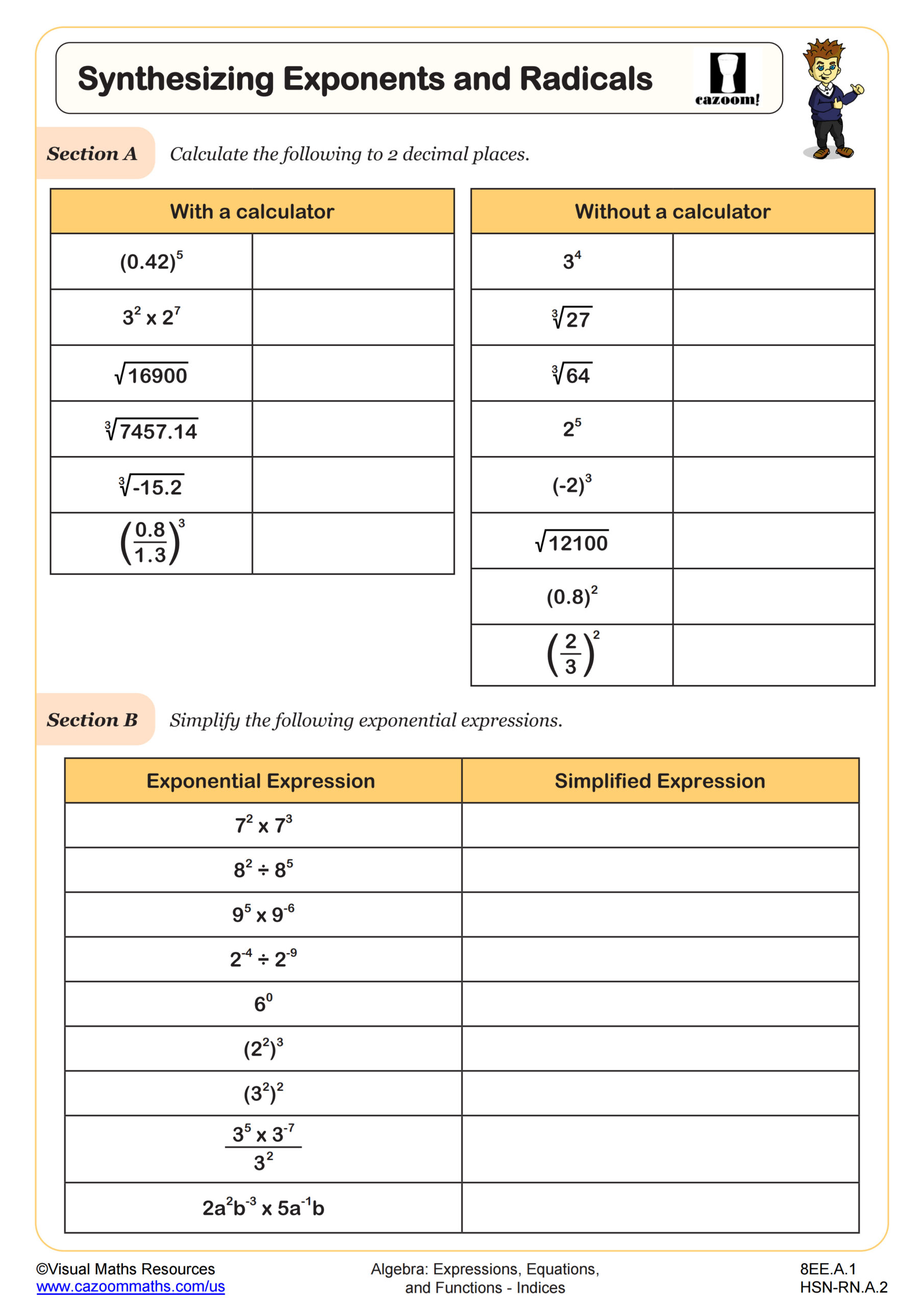
Algebra I indices worksheets address the fundamental exponent properties students need for success throughout high school math, including the product rule, quotient rule, power rule, and zero exponent property. Students practice applying these rules to simplify expressions with positive and negative exponents, then extend their understanding to radicals as fractional exponents. The worksheets align with Common Core standards for working with integer and rational exponents (HSN-RN.A.1, HSN-RN.A.2).
Teachers often observe that students lose points by applying the product rule when they should use the power rule, particularly with expressions like (x³)⁴ versus x³ · x⁴. The worksheets provide targeted practice distinguishing between these scenarios through varied problem types that require students to identify which rule applies before simplifying. This deliberate scaffolding helps students develop the pattern recognition skills necessary for more complex algebraic manipulation.
How Do Indices Appear on the SAT and ACT?
Standardized tests like the SAT and ACT regularly include questions requiring students to simplify exponential expressions, often embedded within larger algebraic problems rather than as isolated simplification exercises. Students must recognize when to apply exponent rules while solving equations, manipulating formulas, or working with scientific notation. The ACT particularly tests negative exponents and fractional exponents within real-world contexts, while the SAT calculator section often presents these concepts algebraically without numeric values.
Students lose points when they incorrectly simplify expressions with negative exponents by making the entire term negative rather than finding the reciprocal. Another frequent error occurs when students add exponents during multiplication but forget to multiply them during exponentiation. Teachers notice that students who practice converting between radical and exponential notation perform significantly better on test questions involving rational exponents, as this flexibility allows them to choose whichever form makes the problem easier to solve.
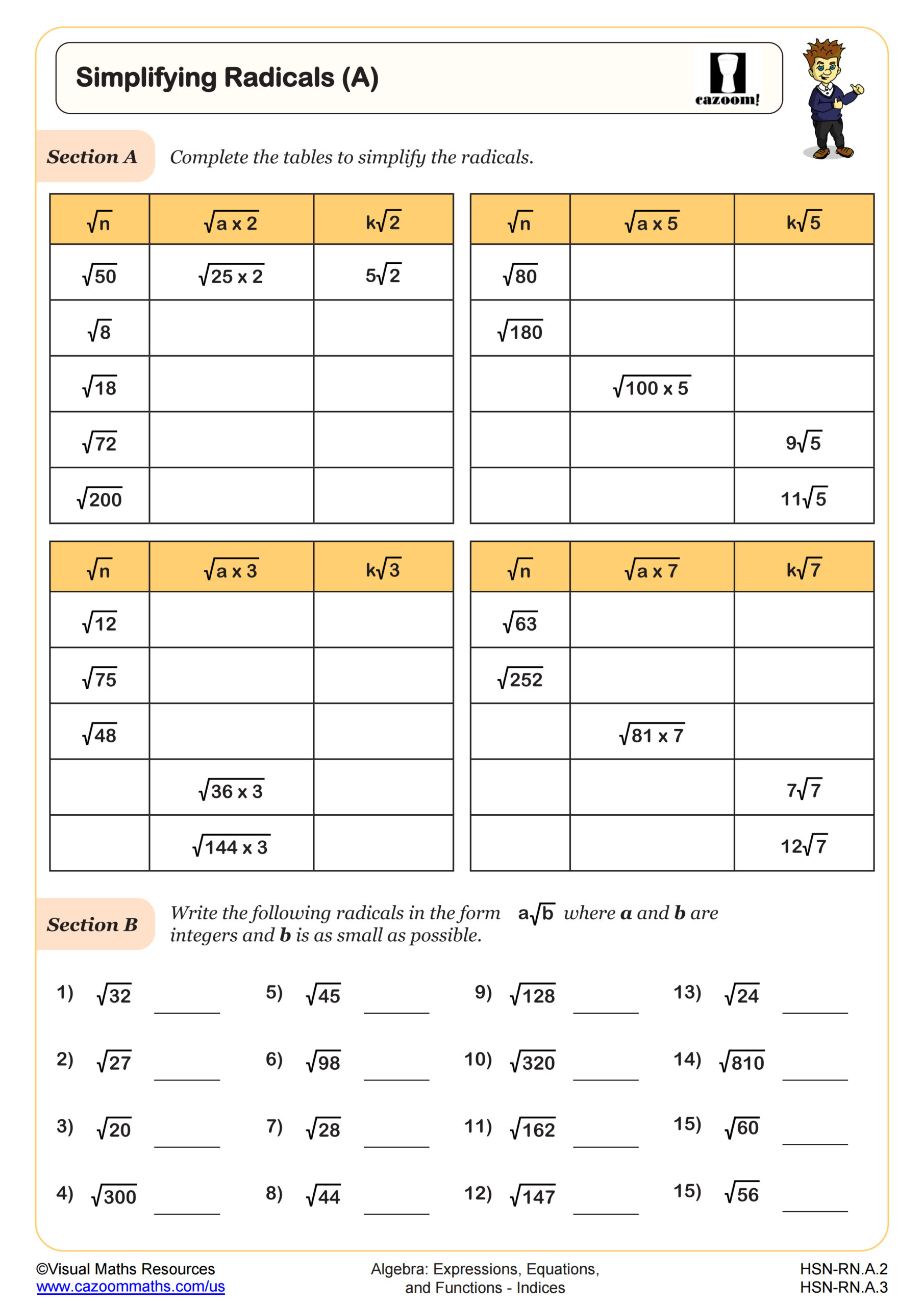
What Strategy Works Best for Simplifying Radicals?
Simplifying radicals requires students to identify perfect square factors (or perfect cube factors for cube roots) within the radicand, then apply the product property of radicals to separate them. The systematic approach involves factoring the radicand into prime factors, grouping pairs of identical factors, and moving those pairs outside the radical as single factors. Students confidently tackle radical simplification once they recognize this process as the reverse of squaring numbers, connecting it to their earlier work with perfect squares and multiplication.
This skill appears extensively in STEM fields, particularly when working with distance formulas in physics, standard deviation calculations in statistics, and geometric applications involving the Pythagorean theorem. Engineers routinely simplify radicals when calculating dimensions, determining load capacities, and analyzing waveforms. College-bound students benefit from automaticity with radical simplification since it reappears in trigonometry when working with special right triangles, in Pre-Calculus with complex numbers, and in Calculus when finding derivatives and integrals involving square roots.
How Should Teachers Use These Indices Worksheets in Algebra I?
The worksheets progress through increasing complexity levels, allowing teachers to differentiate instruction based on student readiness. The scaffolded structure works well for introducing one exponent rule at a time before combining multiple properties in synthesis problems. Teachers find that starting with the basic simplification worksheets, then advancing to negative indices, and finally tackling radical simplification helps students build confidence while preventing the cognitive overload that occurs when too many new concepts appear simultaneously.
Many teachers assign these worksheets as warm-up activities to maintain skill retention throughout the year, since exponent rules appear in nearly every subsequent Algebra I unit. The answer keys make them practical for independent practice stations, homework assignments with immediate feedback, or paired work where students check each other's solutions and discuss errors. The worksheets also serve effectively as targeted intervention for students preparing for unit assessments or state tests, allowing teachers to identify specific misconceptions and address them before summative evaluations.