Algebra I Inequalities Worksheets
Add and Subtract in Standard Form

Add and Subtract Radicals and Rational Exponents

Graphing Inequalities (A)
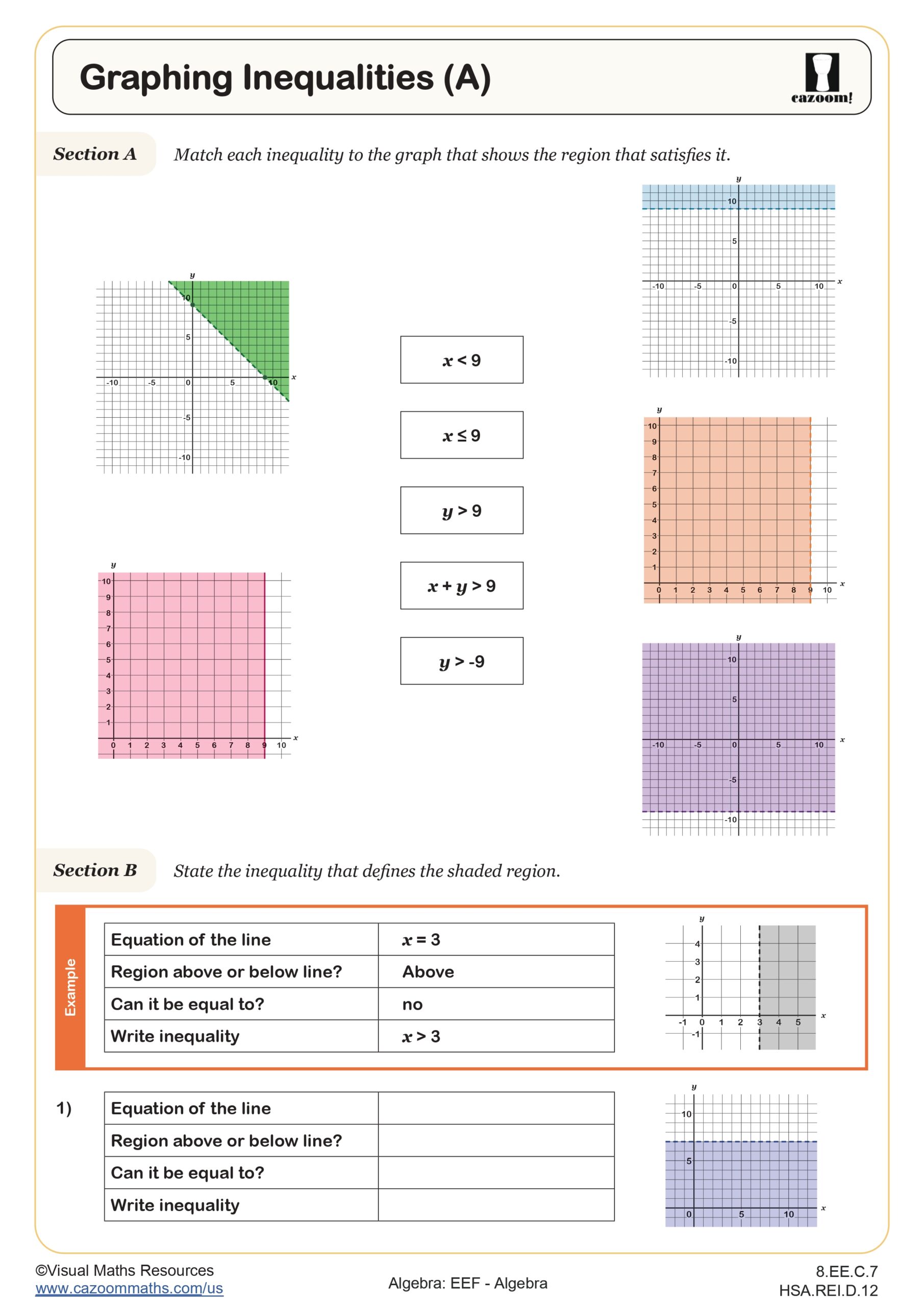
Graphing Inequalities (B)
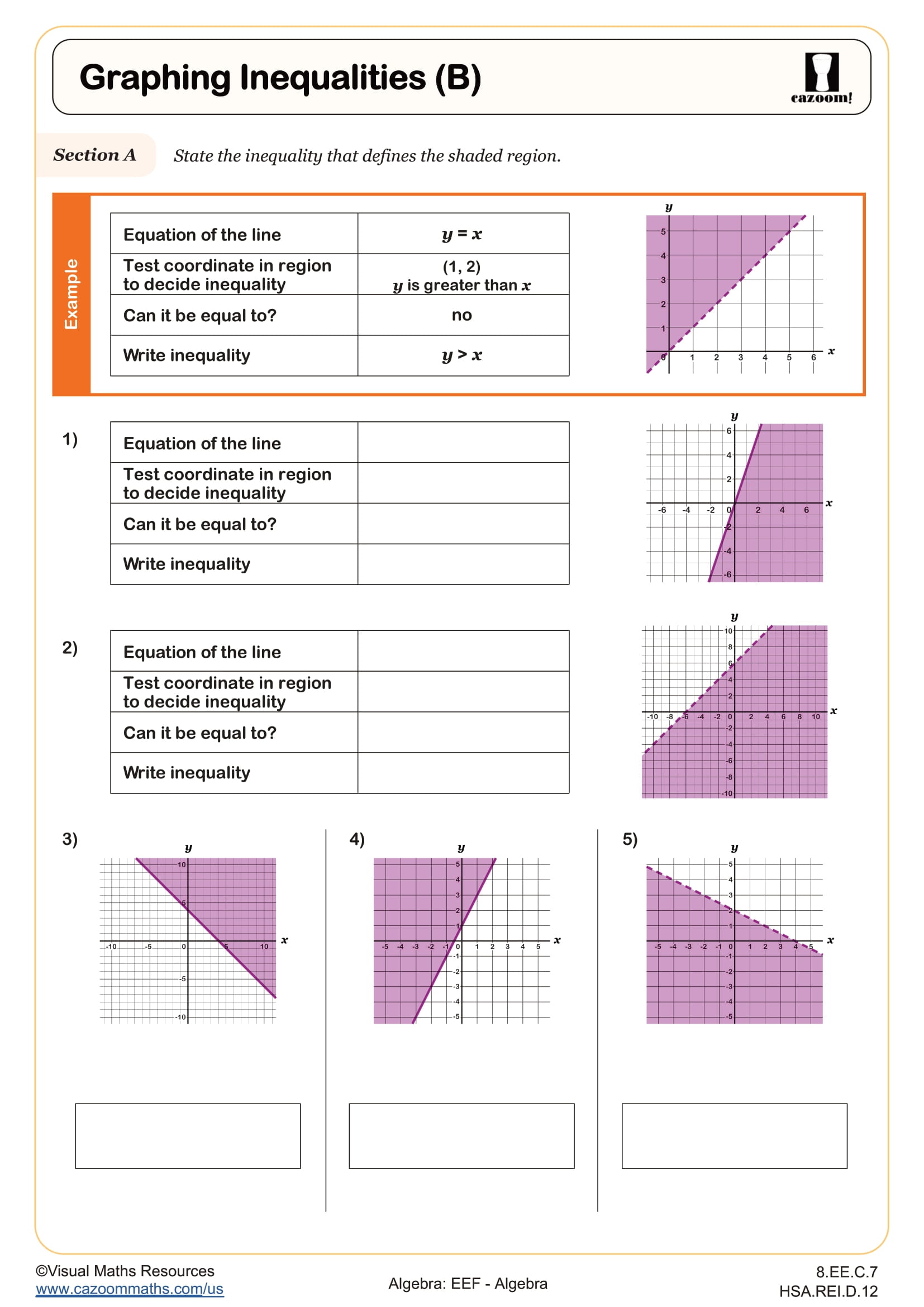
Graphing Inequalities (C)
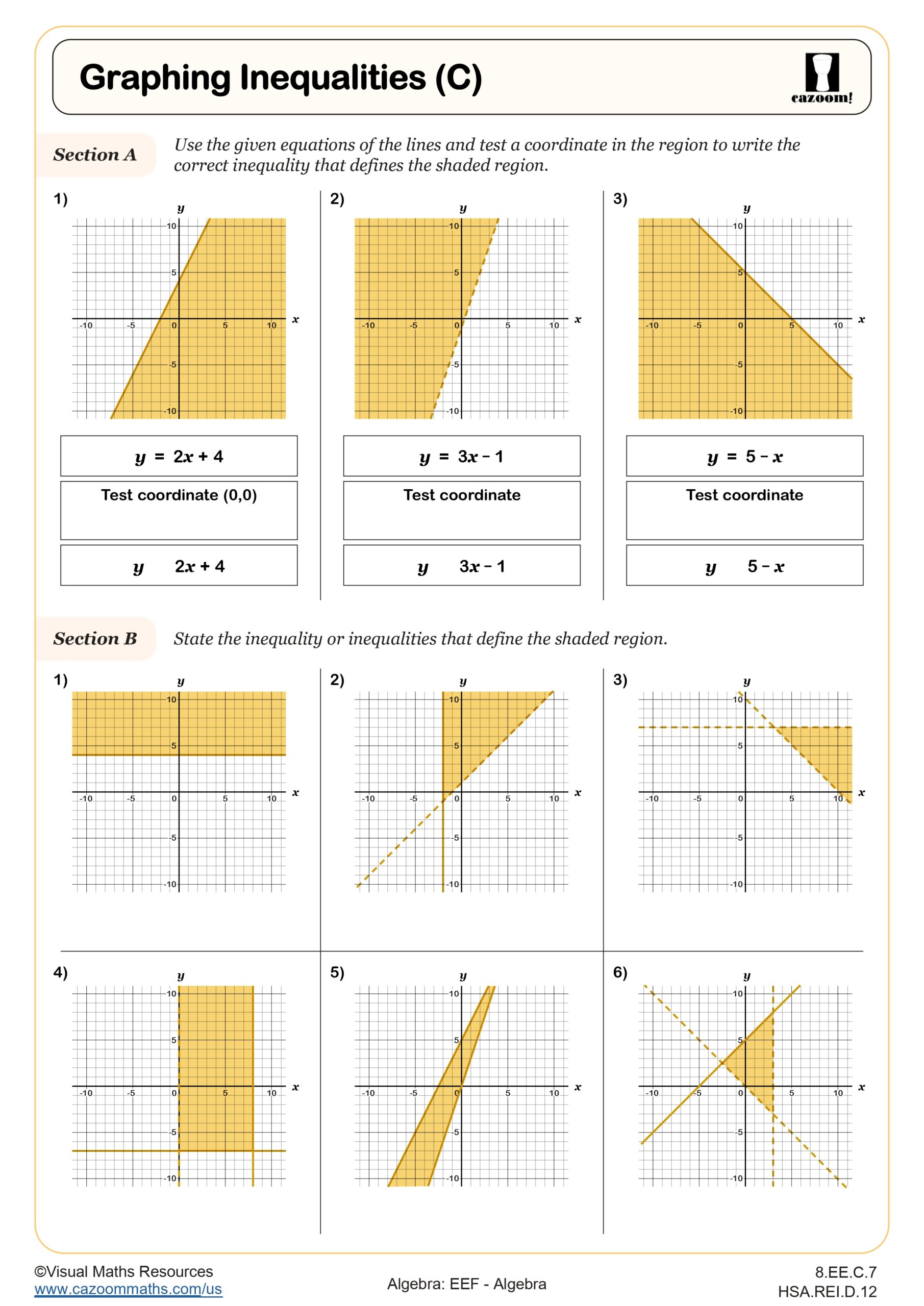
Solving Inequalities (A)

Solving Inequalities (B)

Solving Inequalities (C)

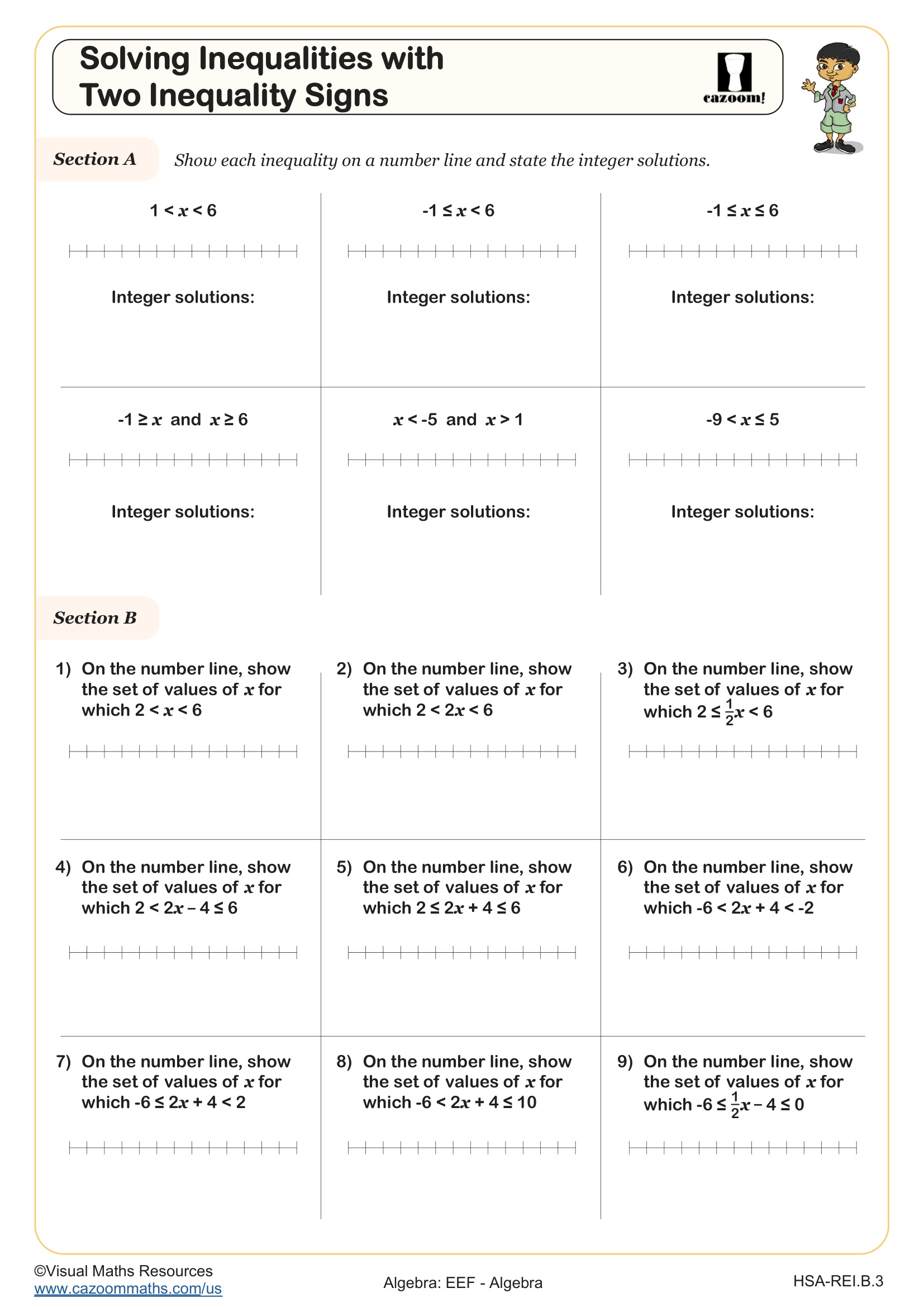
Solving Inequalities with Two Inequalitity Signs
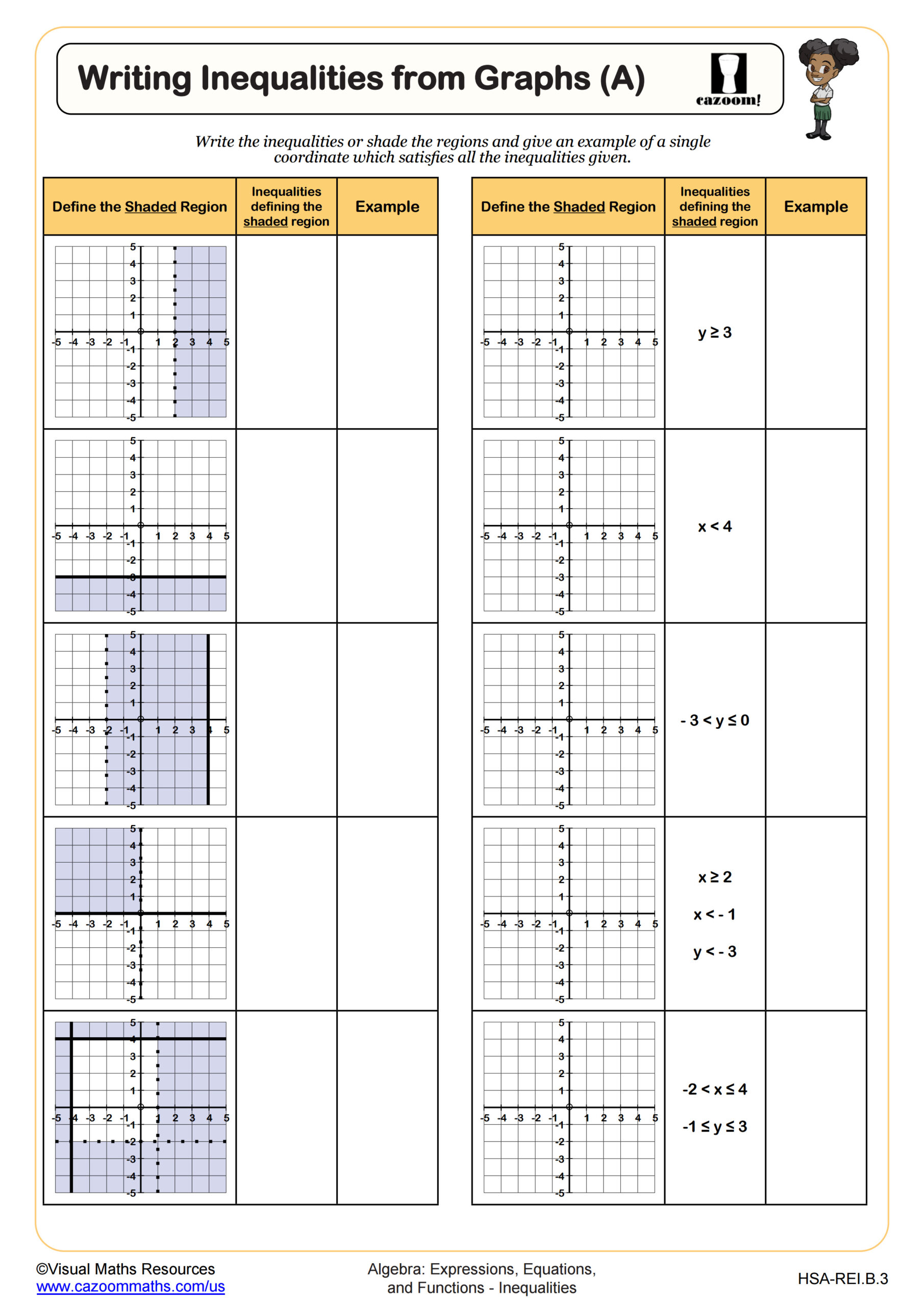
Writing Inequalities from Graphs (A)
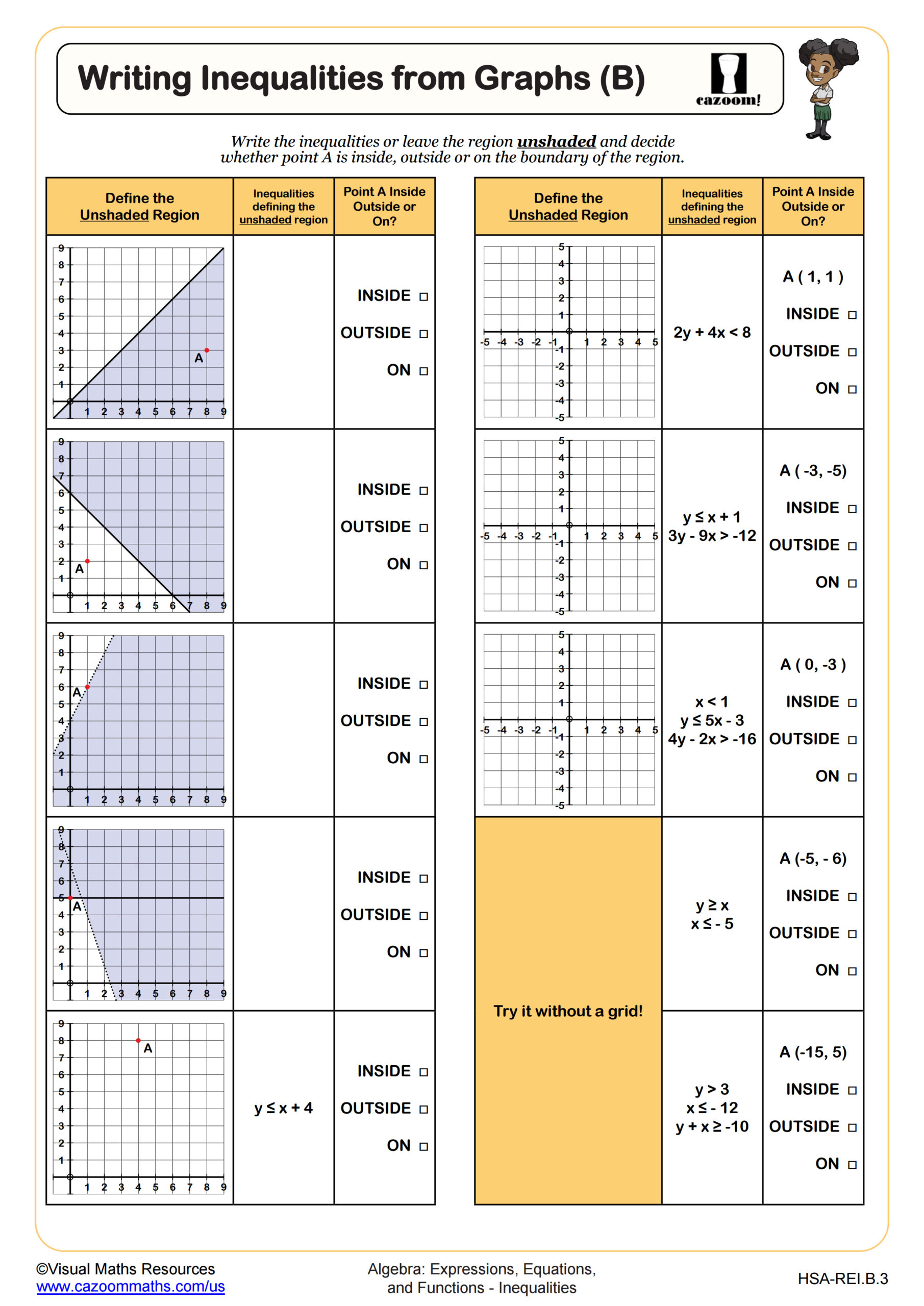
Writing Inequalities from Graphs (B)
What Do Algebra I Inequalities Worksheets Cover?
Algebra I inequalities worksheets address solving one-variable inequalities, graphing solutions on number lines, writing inequalities from graphs, and working with compound inequalities that involve two inequality signs. Students practice applying inverse operations while maintaining inequality relationships, identifying when to reverse inequality symbols, and representing solution sets using both interval notation and graphical methods. The worksheets progress from basic one-step inequalities through more complex multi-step problems that require distributive property and combining like terms.
A common error pattern emerges when students treat inequality symbols exactly like equal signs, forgetting that multiplying or dividing both sides by a negative number requires reversing the direction. Teachers frequently notice students write correct numerical answers but mark solutions incorrectly on number lines, confusing open and closed circles or shading in the wrong direction. Targeted practice with graphing helps students develop the visual reasoning needed to check their algebraic work against what makes mathematical sense.
How Do Inequalities Appear on the SAT and ACT?
Standardized tests like the SAT and ACT regularly include inequality problems in both multiple-choice and grid-in formats, testing students' ability to solve inequalities algebraically, interpret graphs, and apply inequality concepts to word problems. Test questions often embed inequalities within real-world contexts like budget constraints, distance relationships, or minimum requirements, requiring students to translate verbal descriptions into mathematical statements before solving. Both tests expect students to recognize equivalent forms of inequalities and identify solution sets from multiple representations.
Students lose points when they solve inequalities correctly but select answer choices that don't match the proper notation or interval representation. Another frequent mistake involves reversing inequality symbols at the wrong step or failing to reverse them when required, particularly in multi-step problems where negative coefficients appear midway through the solution process. Test-takers also struggle with compound inequality questions that ask which values satisfy both conditions simultaneously, often selecting values that meet only one part of the compound statement.
What Are Compound Inequalities and Why Do They Matter?
Compound inequalities involve two inequality statements connected by "and" or "or," requiring students to find values that satisfy either both conditions simultaneously or at least one condition. An "and" compound inequality like -3 < x ≤ 5 identifies values between two boundaries, while an "or" compound inequality like x < -2 or x > 4 describes values in either of two separate regions. Students solve these by isolating the variable while maintaining the relationship between all three parts of the inequality, particularly in problems written as a single statement with two inequality signs.
Compound inequalities model countless real-world situations in engineering, quality control, and data science. Manufacturing specifications often require measurements to fall within acceptable ranges, such as bolt diameters between 0.248 and 0.252 inches for proper fit. Temperature control systems in laboratories maintain conditions within specific bounds, medical dosages must stay within safe minimums and maximums, and acceptable pH levels for drinking water fall between 6.5 and 8.5. These applications demonstrate why STEM fields rely heavily on inequality reasoning to establish parameters and safety thresholds.
How Can Teachers Use These Inequality Worksheets Effectively?
These worksheets support differentiated instruction by offering problems that range from foundational inequality solving through more challenging applications involving absolute values and compound statements. Teachers can sequence the worksheets to build skills progressively, starting with graphing and writing simple inequalities before advancing to algebraic solutions. The included answer keys enable students to check their work independently during practice sessions, making the worksheets valuable for self-paced learning or flipped classroom models where students work through initial concepts before class discussion.
Many teachers use these worksheets as warm-up activities to maintain inequality fluency throughout the school year, even after the unit concludes, since the skills transfer to later topics like systems of inequalities and quadratic inequalities in Algebra II. The worksheets work well for intervention with students who struggle to distinguish between equation-solving and inequality-solving procedures, providing focused repetition without overwhelming cognitive load. Paired work sessions where students compare their graphed solutions and explain their reasoning help identify conceptual gaps that whole-class instruction might miss, particularly regarding boundary points and solution set notation.