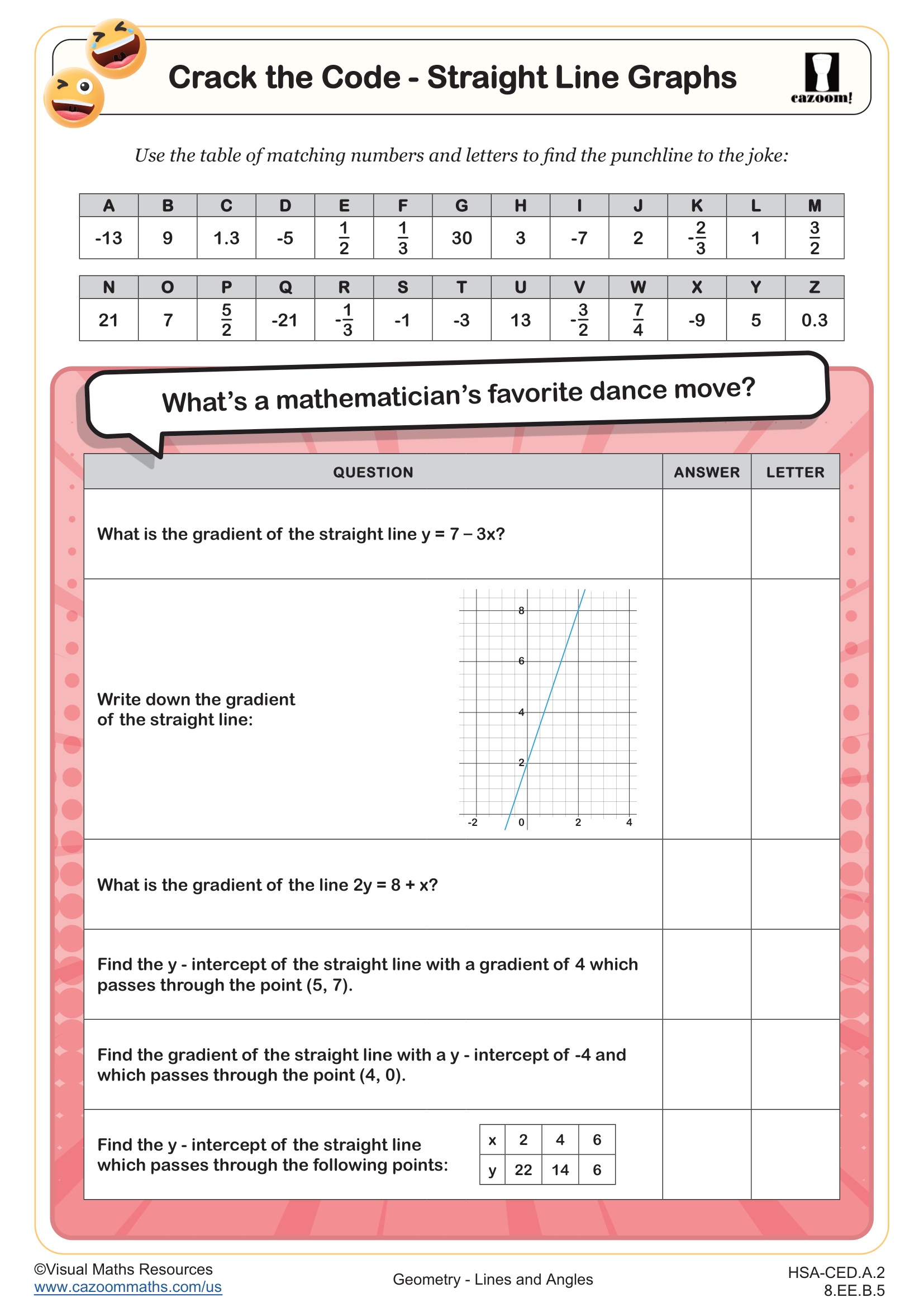
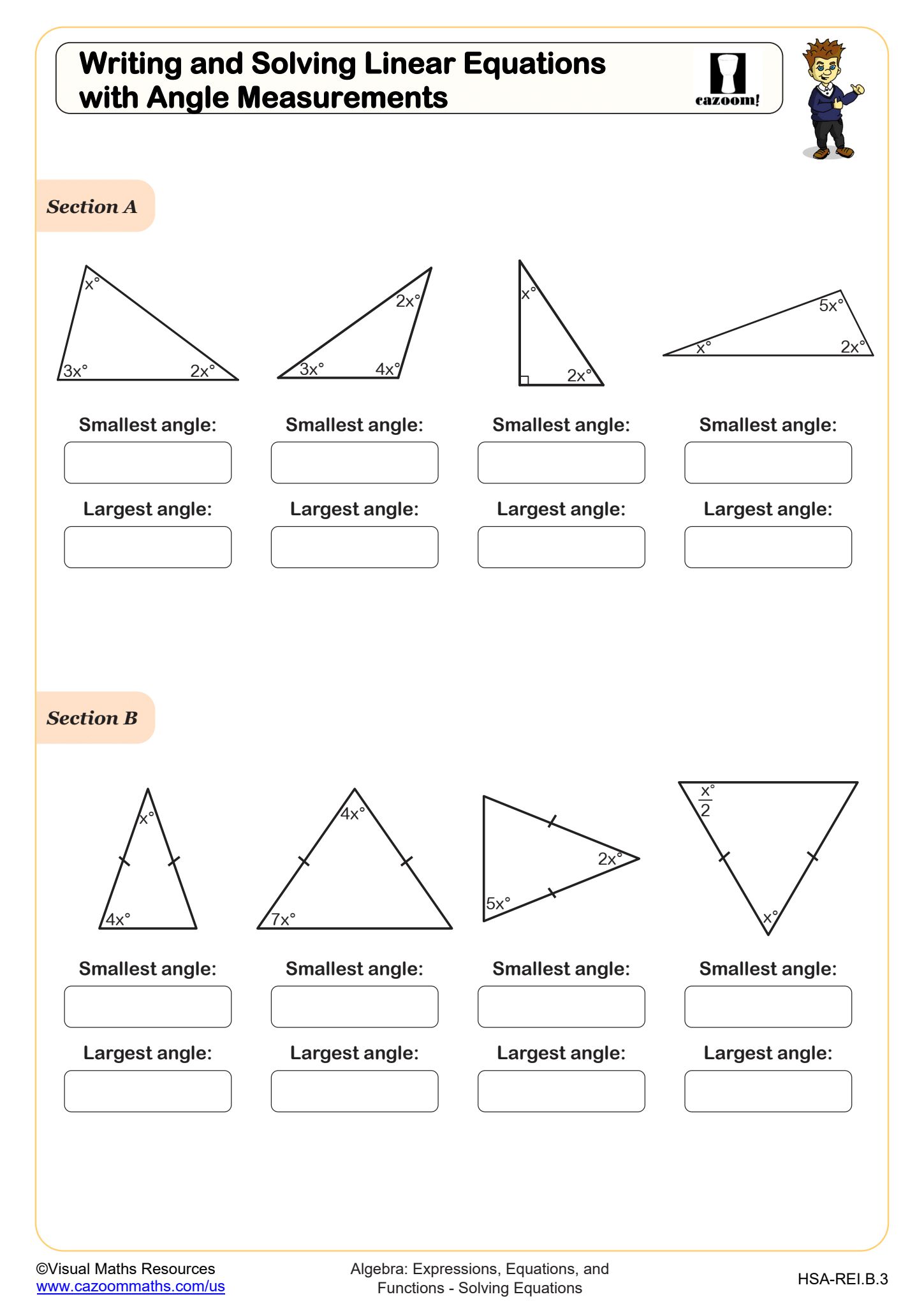
Algebra I Lines and Angles Worksheets
What Do Students Learn in Lines and Angles for Algebra I?
Lines and angles in Algebra I extends beyond basic coordinate graphing to include geometric relationships within the coordinate plane. Students work with parallel and perpendicular lines by analyzing slope relationships, apply angle theorems (supplementary, complementary, vertical angles) to algebraic contexts, and write linear equations based on angle measurements. This topic aligns with Common Core standards for expressing geometric properties with equations and reinforces the connection between algebra and geometry that students will encounter throughout high school mathematics.
Many students initially separate their geometry knowledge from algebra, not recognizing that angle relationships can generate linear equations. Teachers observe that students often correctly identify angle pairs but struggle to translate those relationships into algebraic expressions. For example, when given that two angles are supplementary and one angle measures (3x + 20)°, students may forget to set up the equation (3x + 20) + angle2 = 180 before solving.
How Are Lines and Angles Tested on the SAT and ACT?
Standardized tests frequently combine coordinate geometry with angle relationships in multi-step problems. The SAT expects students to determine whether lines are parallel or perpendicular by comparing slopes, find missing angle measures using algebraic expressions, and apply properties of angles formed by transversals cutting parallel lines. ACT problems often present diagrams where students must write equations from angle relationships, then solve for variables and substitute back to find specific measurements. Both tests assess whether students can move fluidly between geometric visualization and algebraic manipulation.
Students lose points when they correctly solve for a variable but forget the question asks for an angle measurement requiring substitution. Another common error occurs when students confuse negative reciprocal slopes (perpendicular lines) with simply negative slopes. Test-taking students also struggle when angle diagrams appear on coordinate grids, requiring them to calculate slopes from coordinates and then apply angle theorems—this integrated thinking separates proficient students from those who memorize procedures in isolation.
How Do Students Use Slope to Identify Parallel and Perpendicular Lines?
Slope analysis reveals the geometric relationship between lines without requiring measurement tools. Parallel lines maintain constant distance apart, which translates algebraically to identical slopes—if line 1 has slope m = 2/3, any line parallel to it also has m = 2/3. Perpendicular lines intersect at 90° angles, creating slopes that are negative reciprocals of each other: a line with slope 2/3 is perpendicular to any line with slope -3/2. Students practice extracting slopes from equations in various forms (slope-intercept, standard, point-slope) and determining geometric relationships through numerical comparison rather than visual estimation.
This skill proves valuable in computer graphics, engineering design, and architecture, where precise perpendicular and parallel relationships are essential. GPS navigation systems use perpendicular line algorithms to calculate shortest distances from points to roads. Urban planners apply these concepts when designing street grids, ensuring roads meet at appropriate angles for safe traffic flow. College-bound students encounter these principles again in calculus when studying normal lines (perpendicular to tangent lines) and in linear algebra when exploring orthogonal vectors.
How Can Teachers Use These Algebra I Worksheets in the Classroom?
These worksheets provide structured practice that builds from identifying slope relationships to writing complex equations involving angle measurements. The code-breaking format engages students who typically disengage during routine practice, while the linear equation problems with angle contexts reinforce the algebra-geometry connection that state assessments emphasize. Answer keys allow students to check their work during independent practice, helping them identify whether errors stem from calculation mistakes or conceptual misunderstandings about slope relationships or angle properties.
Teachers use these resources effectively during review before coordinate geometry unit tests or as intervention materials for students who struggle to connect algebraic and geometric thinking. The worksheets work well for paired problem-solving, where one student solves while the partner checks against the answer key, then they switch roles. Many teachers assign these as homework before assessments covering equations of parallel and perpendicular lines, since students benefit from repeated exposure to problems requiring them to translate between geometric language and algebraic notation.