Algebra I Sequences Worksheets
What Do Algebra I Students Learn About Sequences?
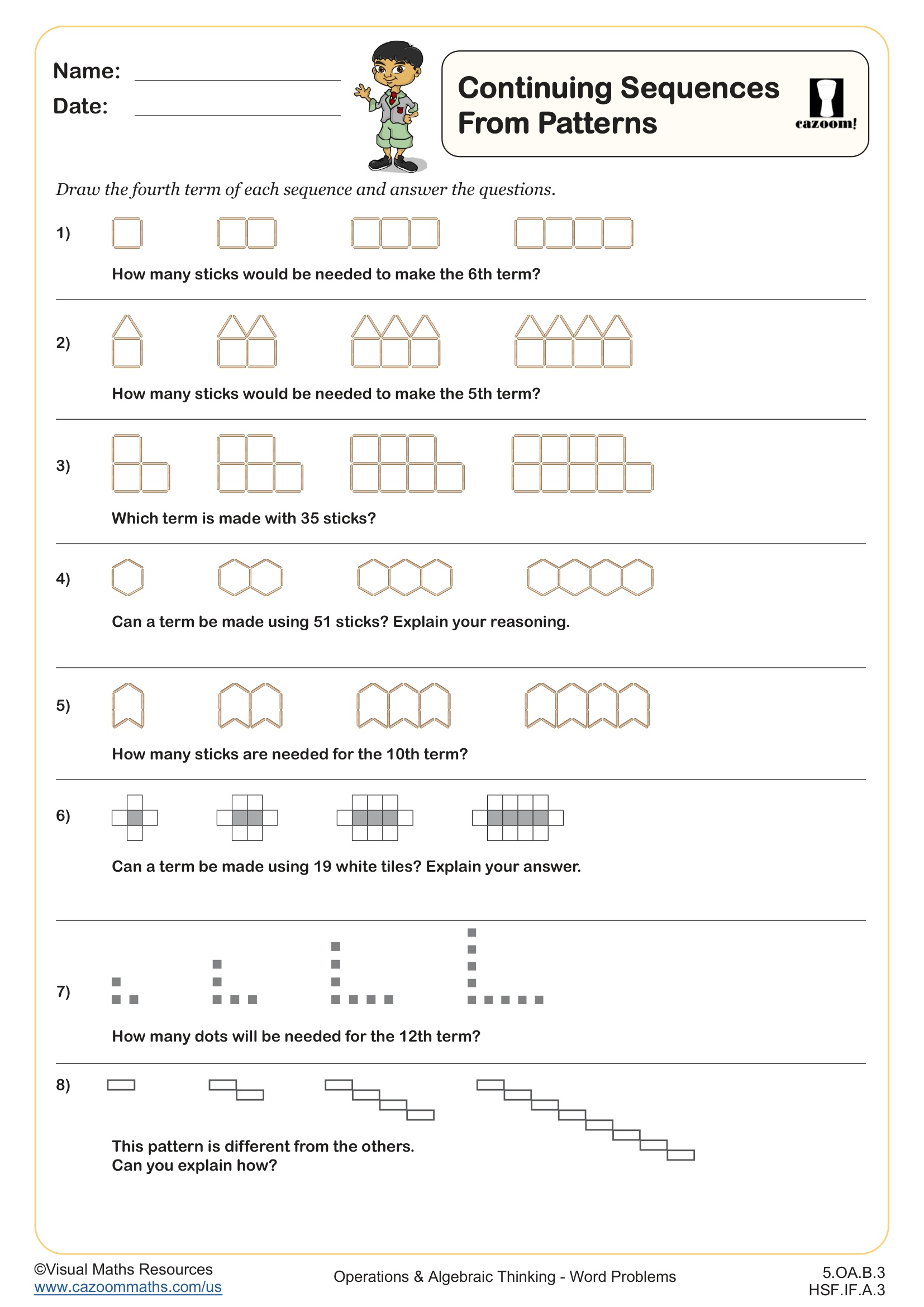
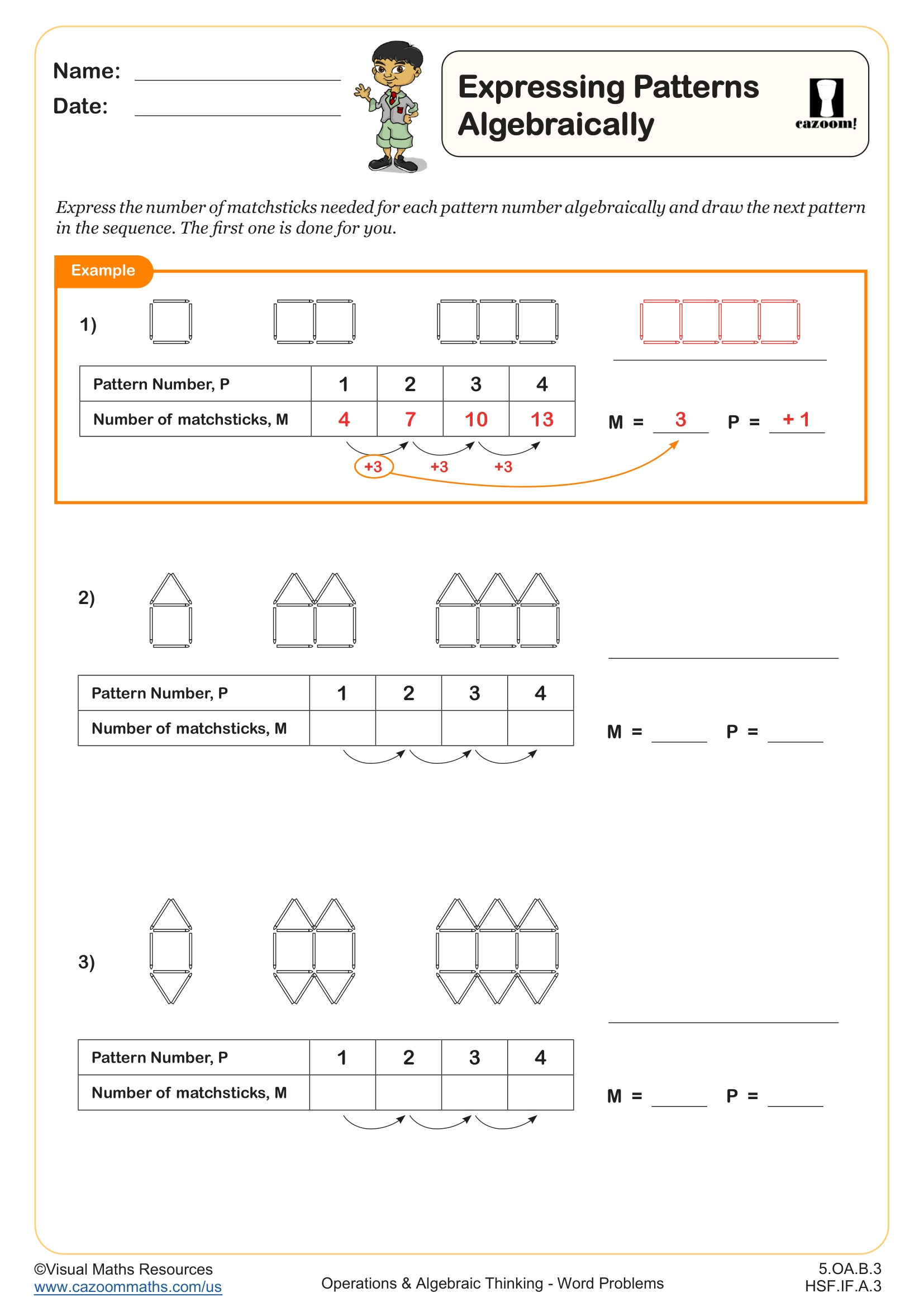
In Algebra I, students learn to identify patterns in sequences, determine the rule governing how terms change, and continue sequences based on those patterns. They practice distinguishing between arithmetic sequences (constant difference) and other pattern types, then move toward expressing these patterns algebraically using nth term notation. This work aligns with Common Core standards for linear functions and introduces the idea that sequences are discrete functions where the domain is positive integers.
A common error occurs when students confuse the term value with its position number. For example, in the sequence 5, 8, 11, 14, students might write the third term as 11 instead of recognizing that n=3 produces the value 11 when using the rule 3n+2. Teachers find that explicitly labeling position versus value in early practice helps students keep these concepts separate and builds accuracy when writing algebraic expressions.
How Do Sequences Appear on the SAT and State Assessments?
Standardized tests like the SAT and ACT often present sequence problems within function notation questions or ask students to determine the nth term of an arithmetic sequence. Test questions might provide the first few terms and ask students to find a specific later term, identify the rule, or recognize whether a given formula matches the sequence. State assessments typically include multiple-choice and short-answer items that require students to continue patterns or write expressions representing sequences.
Students lose points when they calculate the next few terms correctly but fail to generalize the pattern into an algebraic rule. Another frequent mistake involves misapplying formulas for arithmetic sequences, particularly confusing the first term with the common difference. Test-takers who practice translating between numeric patterns and algebraic expressions, then checking their formulas against given terms, perform significantly better on these assessment items.
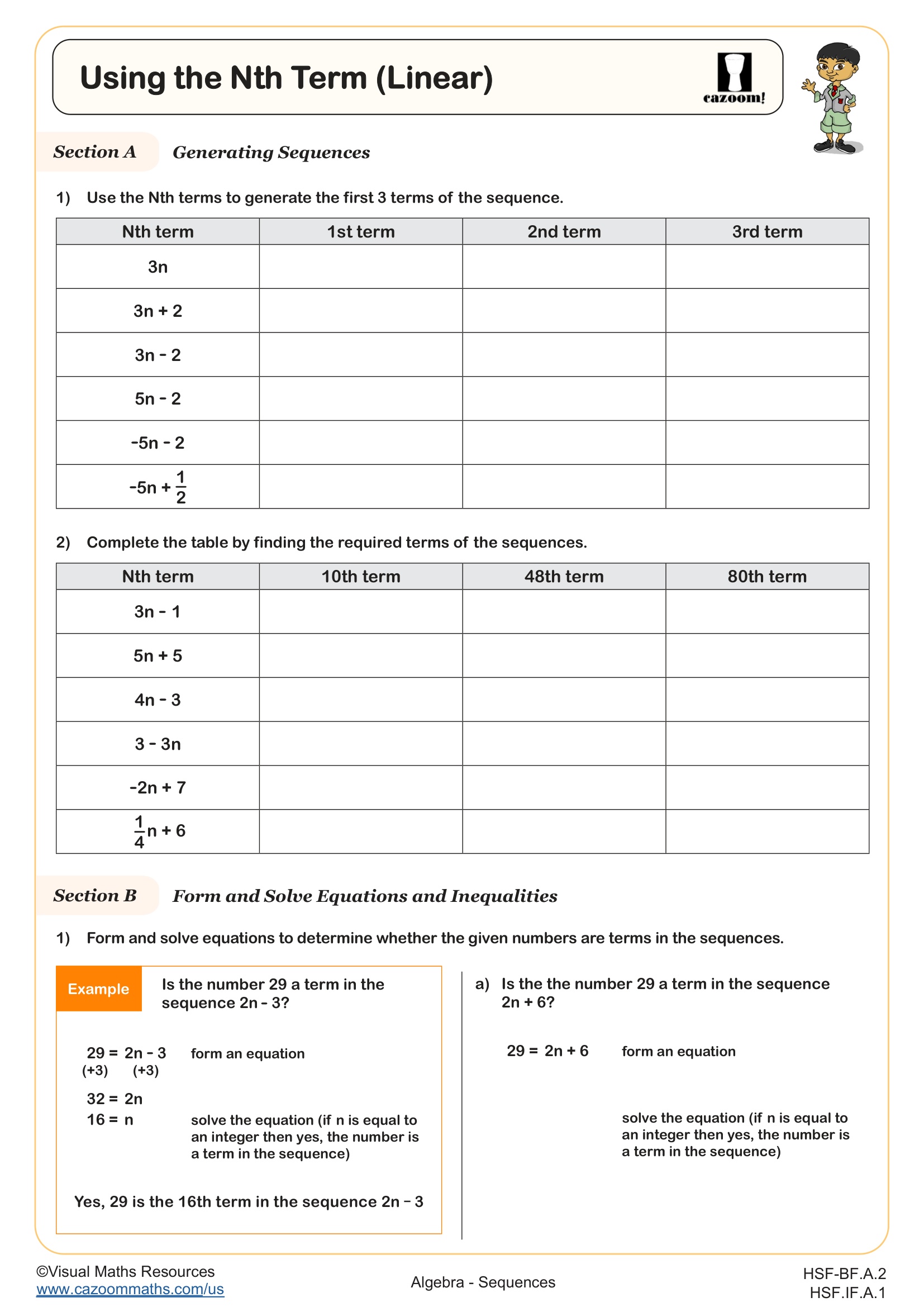
What Is the Nth Term Formula for Linear Sequences?
The nth term formula for a linear (arithmetic) sequence expresses any term's value based on its position number n. The general form is an = a1 + (n-1)d, where a1 represents the first term and d represents the common difference between consecutive terms. In Algebra I, students often work with simplified versions like an = dn + c, which directly shows the relationship as a linear function. Recognizing that arithmetic sequences are linear functions with discrete inputs helps students see the connection between slope and common difference.
This concept appears frequently in STEM contexts, particularly when modeling situations with constant rates of change. Engineers use sequence formulas to calculate material quantities in repetitive structures, while computer scientists apply them in algorithm analysis to predict computation time. Finance applications include calculating loan payments or investment values over fixed periods, making nth term formulas a practical tool beyond pure mathematics coursework and into college-level quantitative fields.
How Can Teachers Use These Sequences Worksheets in Algebra I?
These worksheets provide scaffolded practice that starts with visual and numeric patterns before progressing to algebraic representations and nth term applications. The collection moves from continuing sequences by recognizing patterns to expressing those patterns symbolically, allowing teachers to differentiate instruction based on student readiness. Complete answer keys enable students to check their work independently during practice sessions, while teachers can quickly identify which students grasp pattern recognition versus which need additional support translating patterns into algebraic language.
Many teachers use these worksheets for warm-up activities that activate prior knowledge before introducing new function concepts, or as targeted intervention for students struggling with linear relationships. The materials work well for test preparation since sequences appear regularly on state assessments and college entrance exams. Teachers also find value in assigning different worksheets to small groups, then having students explain their strategies to classmates—this peer discussion often clarifies the connection between numeric patterns and algebraic thinking more effectively than teacher-led instruction alone.