Algebra I Simplification Worksheets
Add and Subtract in Standard Form

Adding and Subtracting Algebraic Fractions

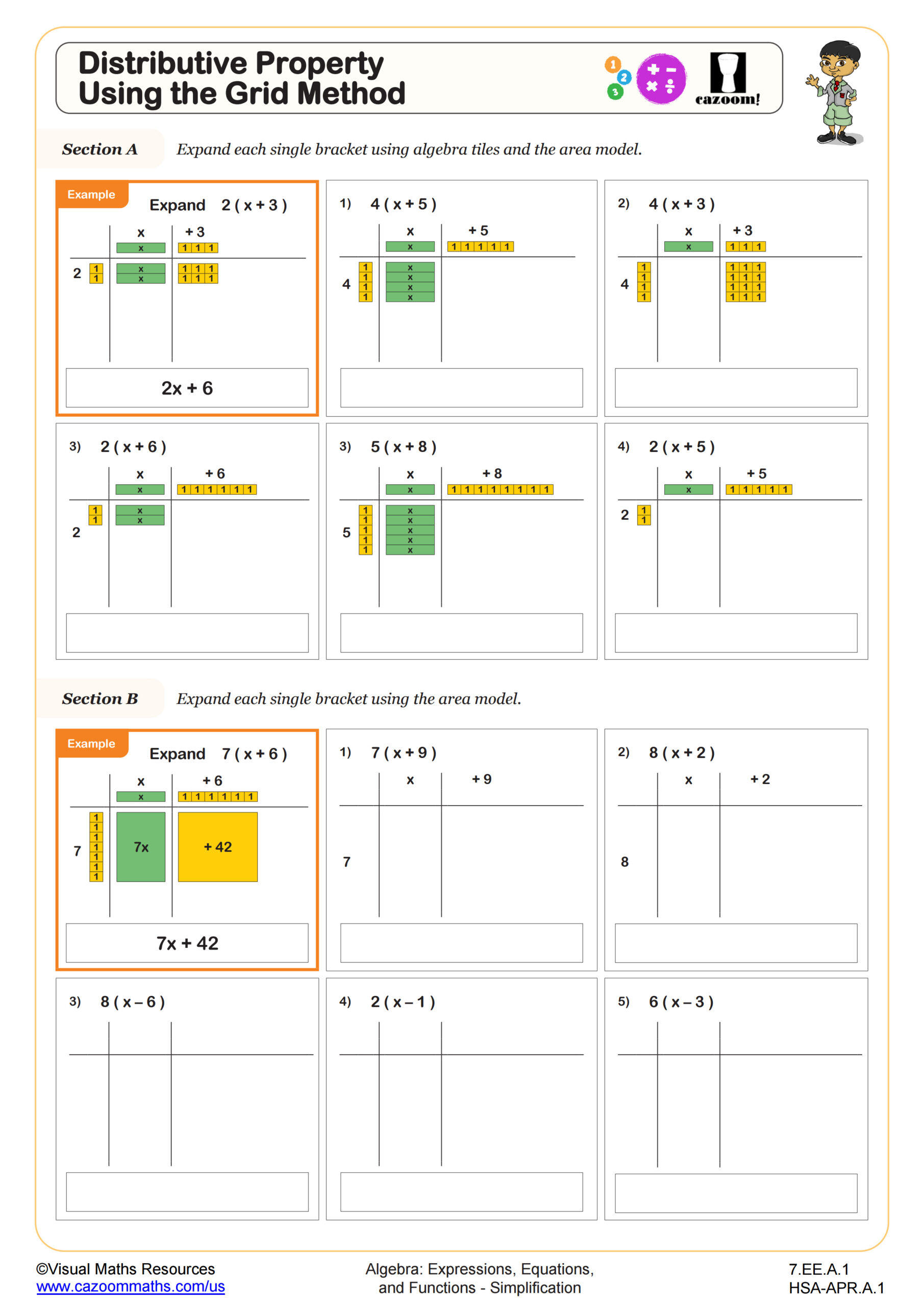
Distributive Property

Distributive Property using the Grid Method
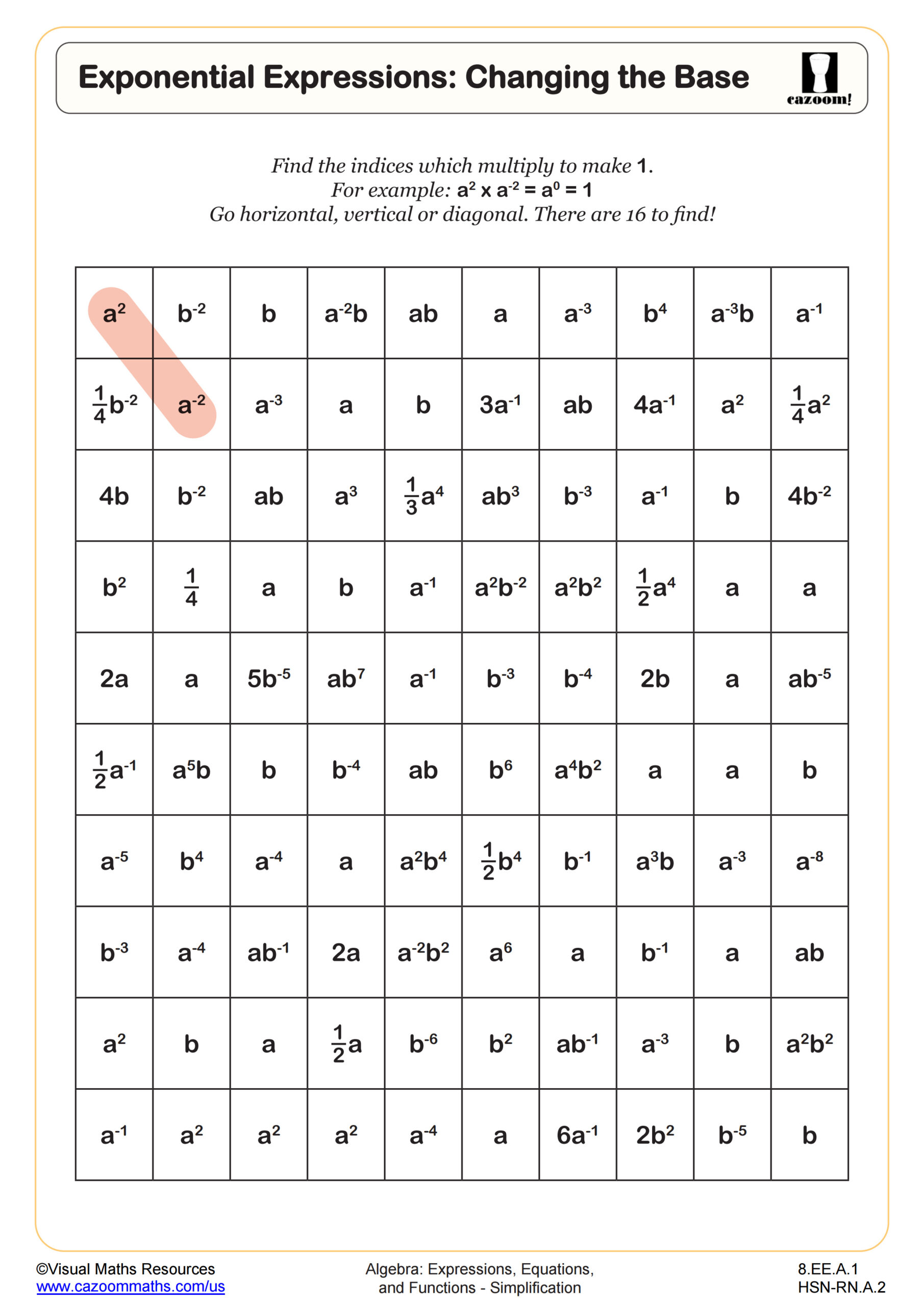
Exponential Expressions: Changing the Base
Factoring Quadratic Expressions

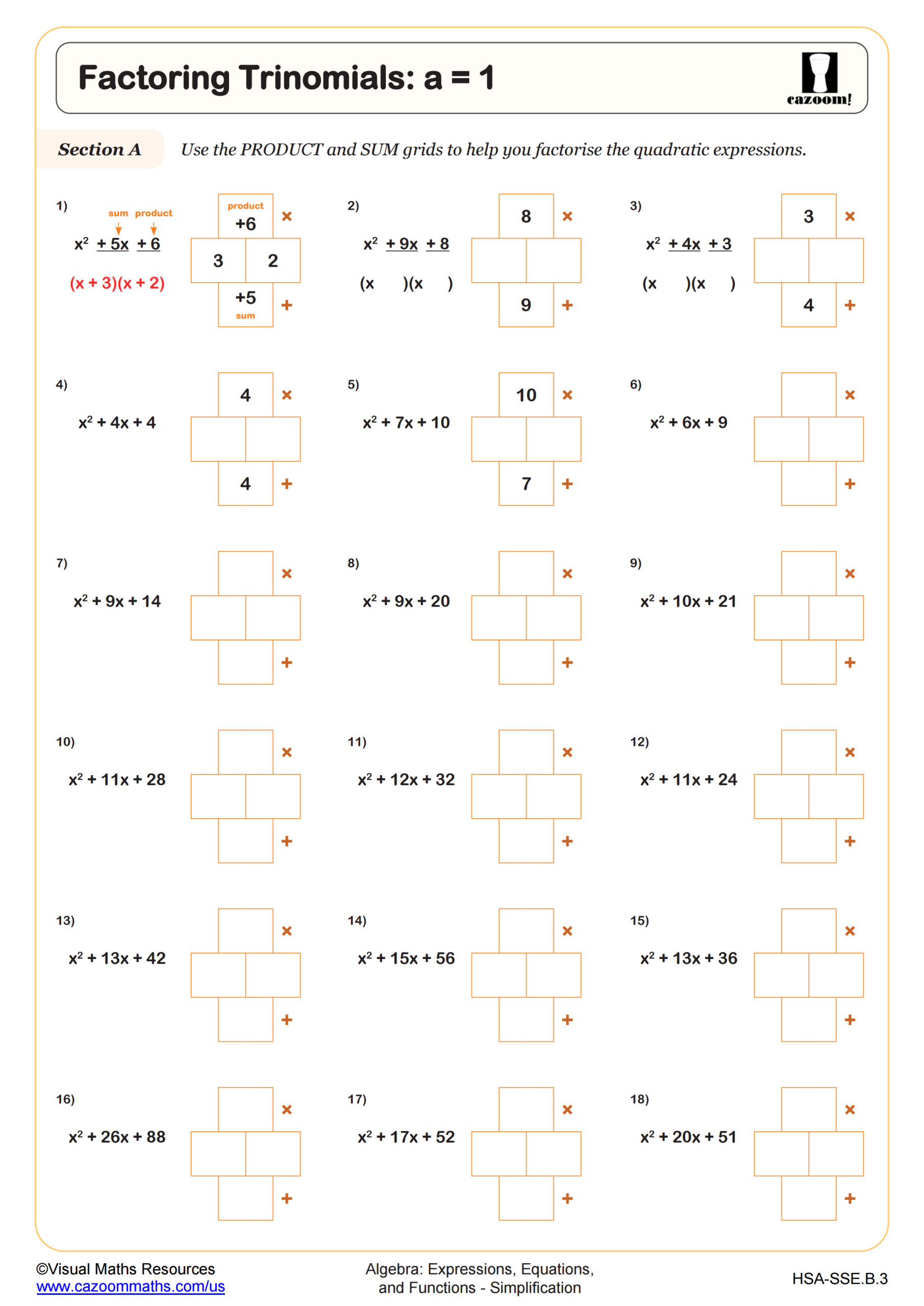
Factoring Trinomials

Factoring Trinomials: a = 1
Factoring using GCF

Factoring: Difference of Two Squares

Greatest Common Factor

Identifying Like Terms

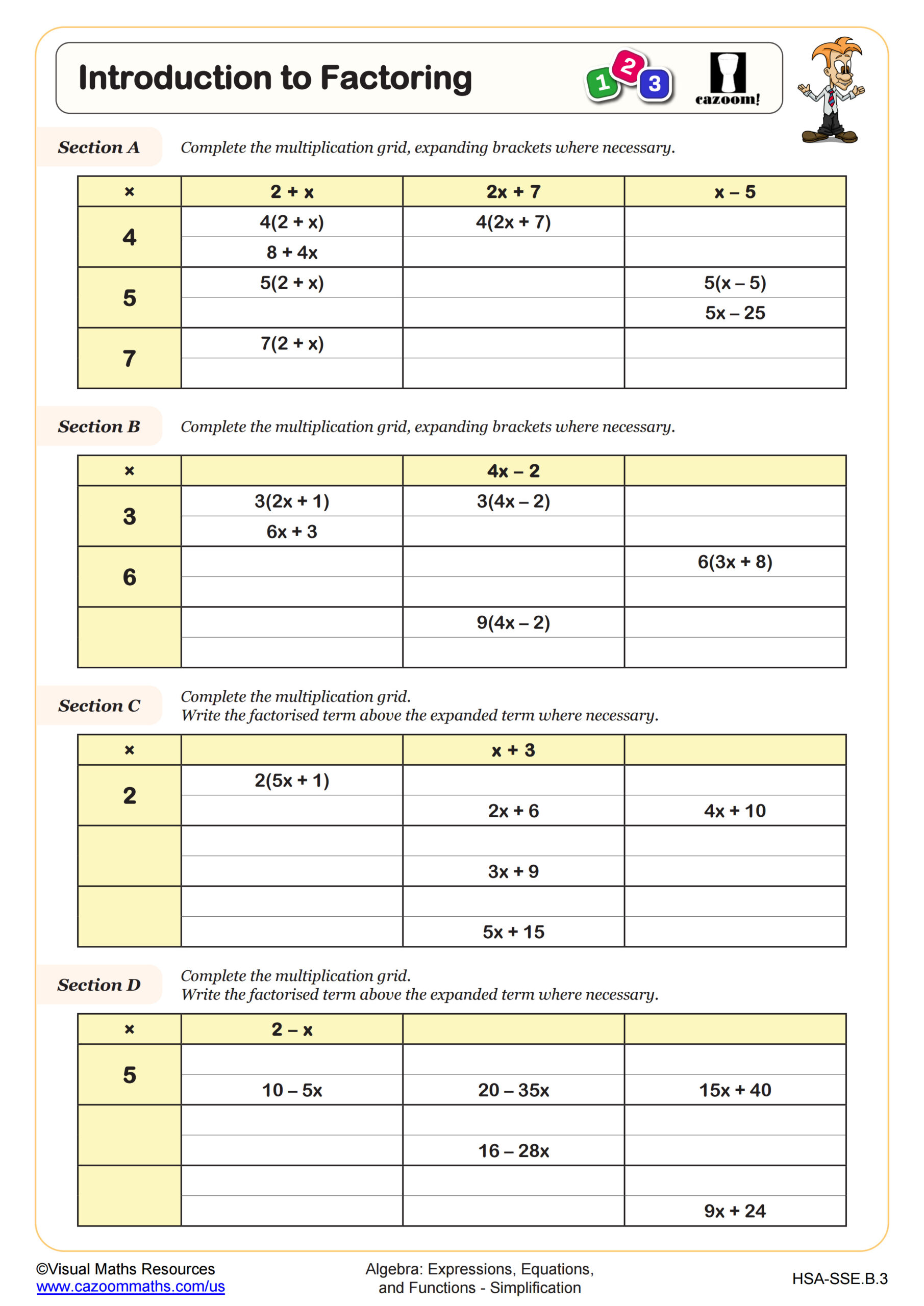
Introduction to Factoring
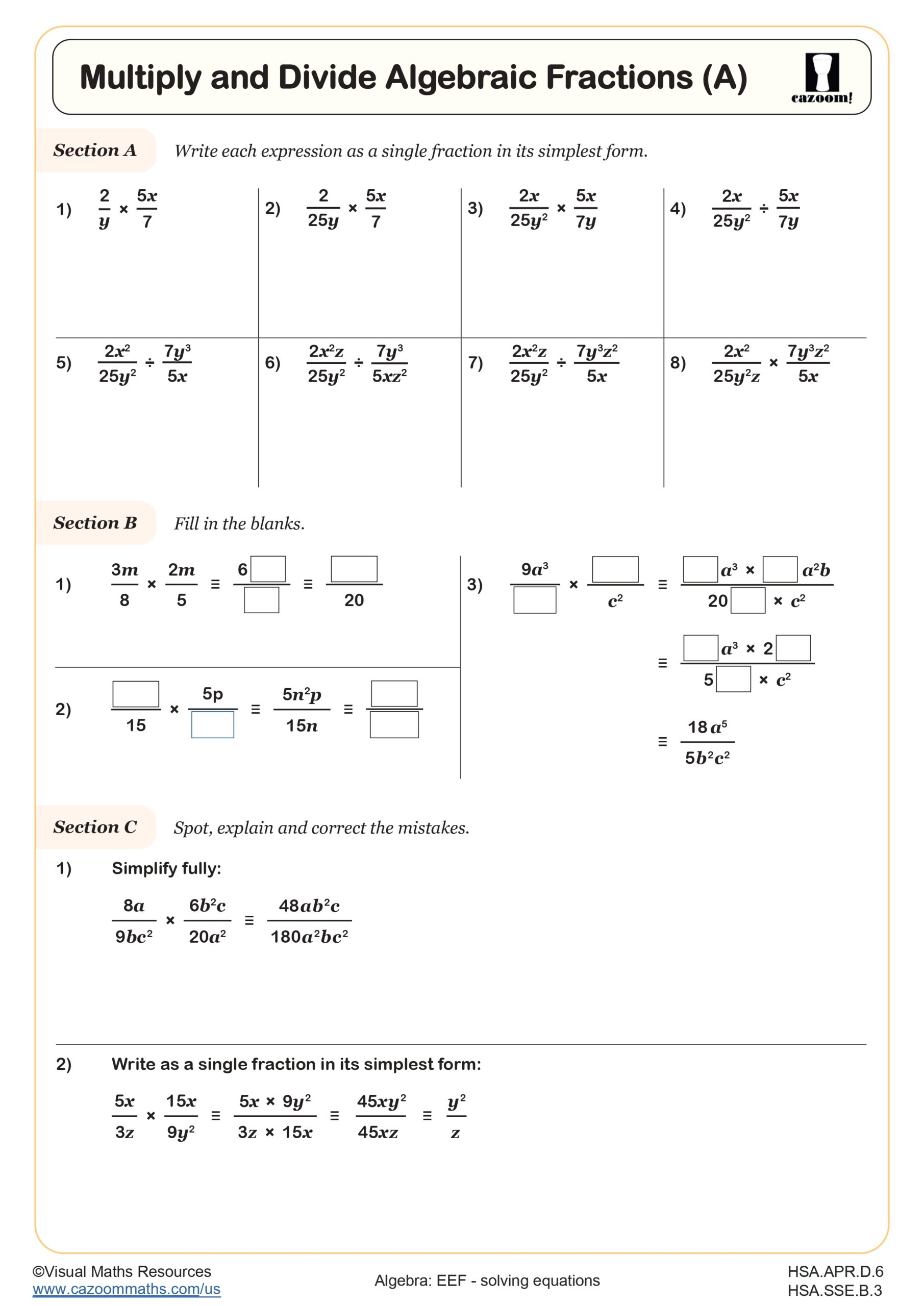
Multiply and Divide Algebraic Fractions (A)
Multiplying and Simplifying Polynomials

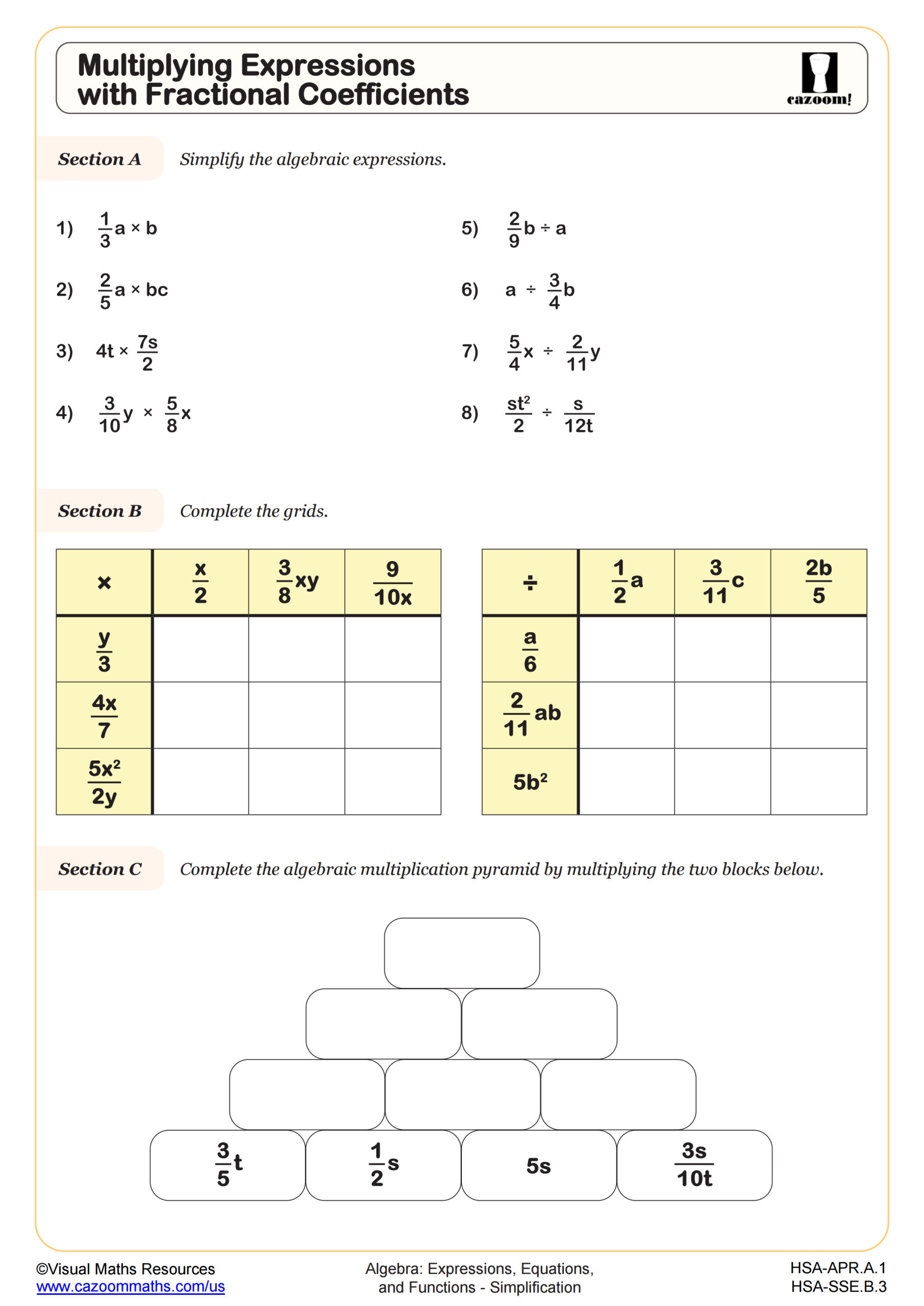
Multiplying Expressions with Fractional Coefficients
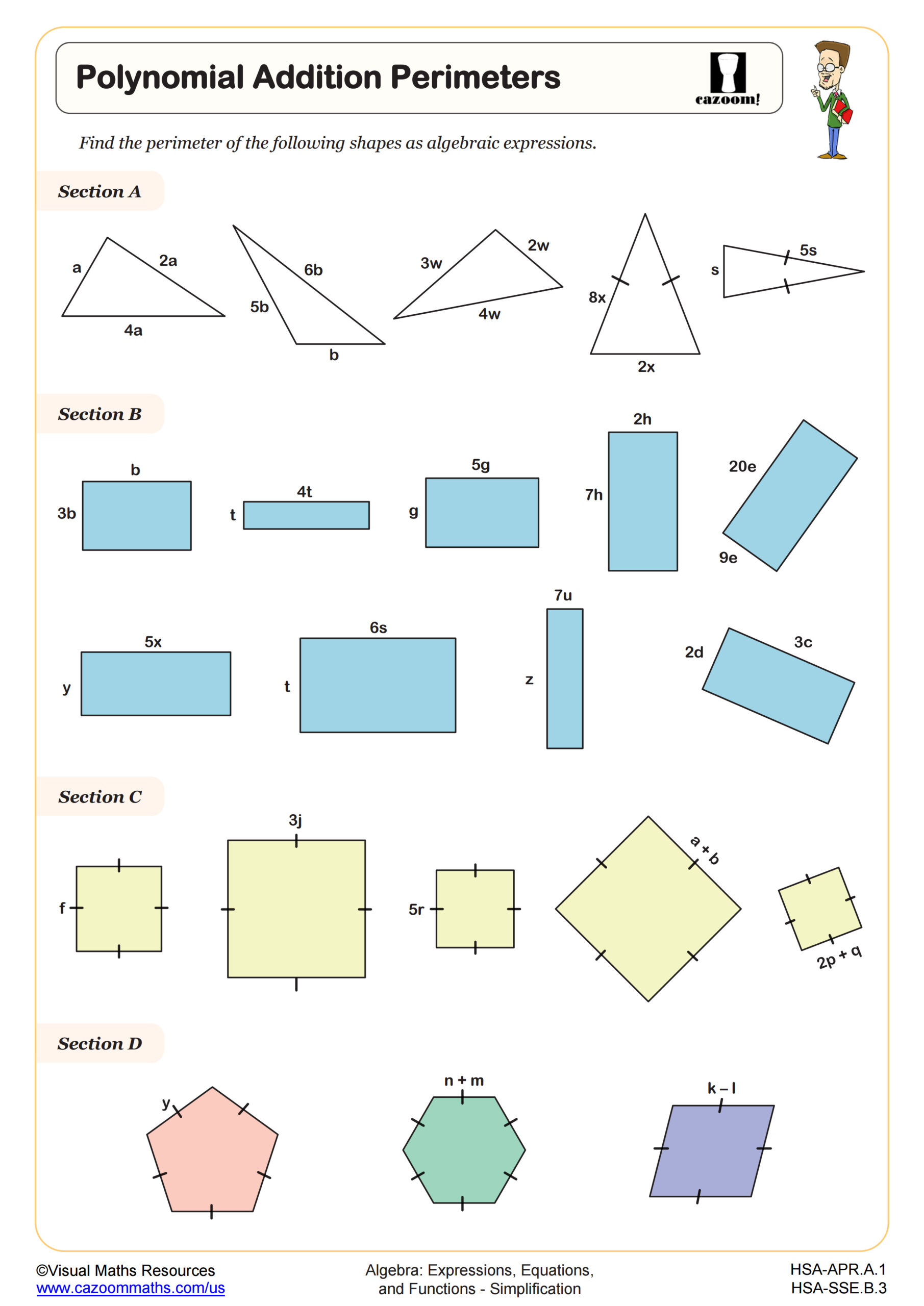
Polynomial Addition Perimeters
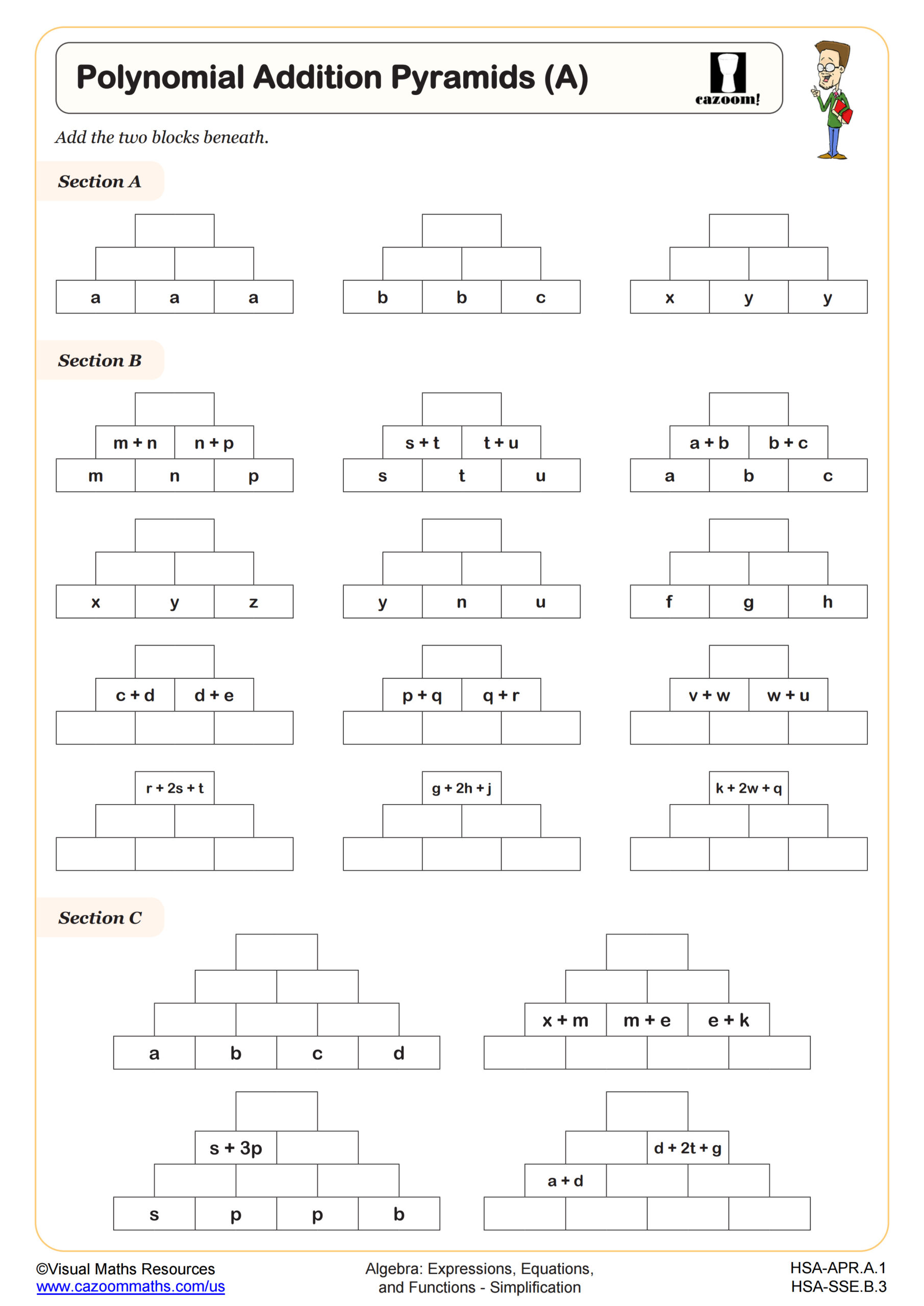
Polynomial Addition Pyramids (A)
Polynomial Addition Pyramids (B)
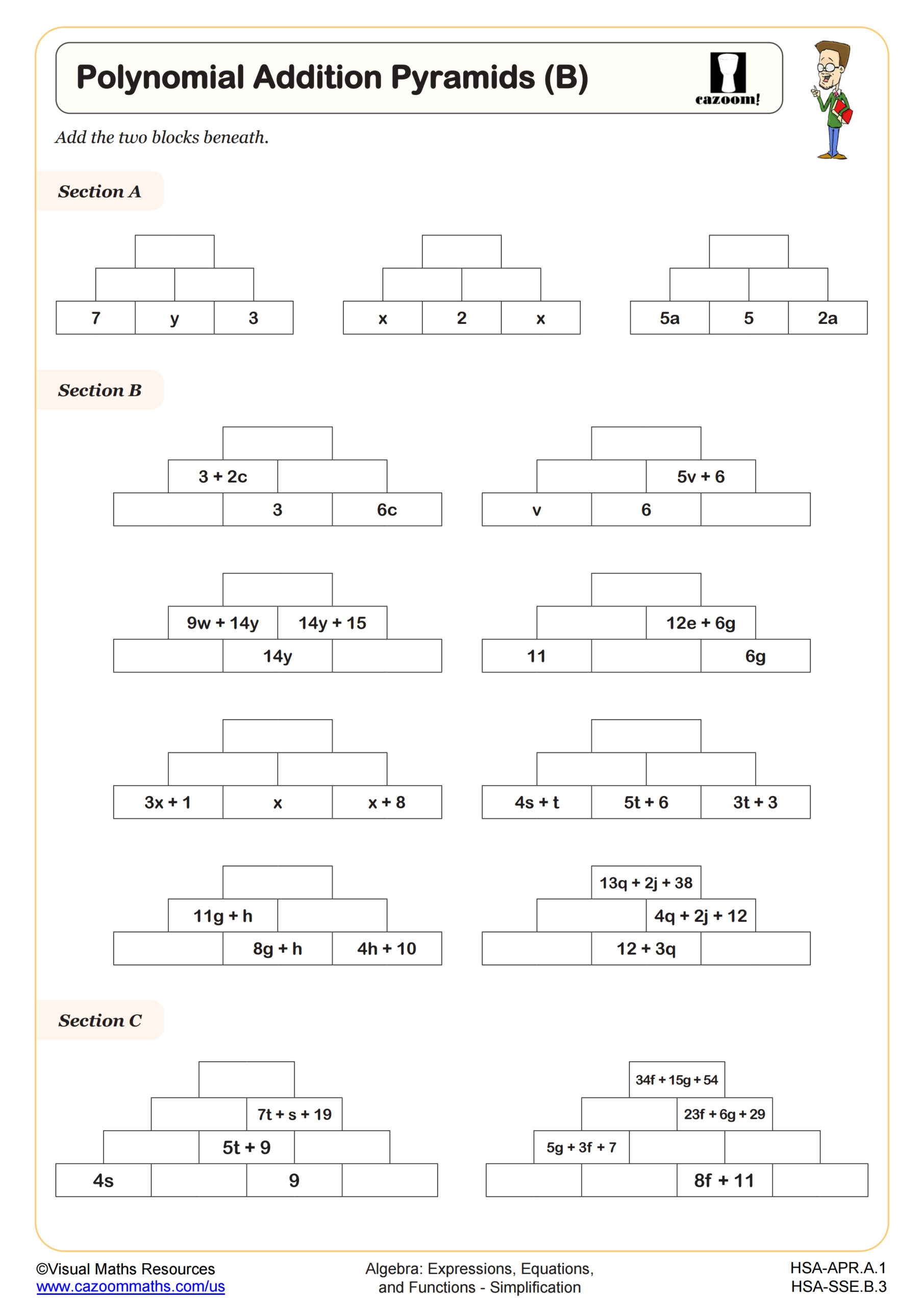
Polynomial Addition Pyramids (C)
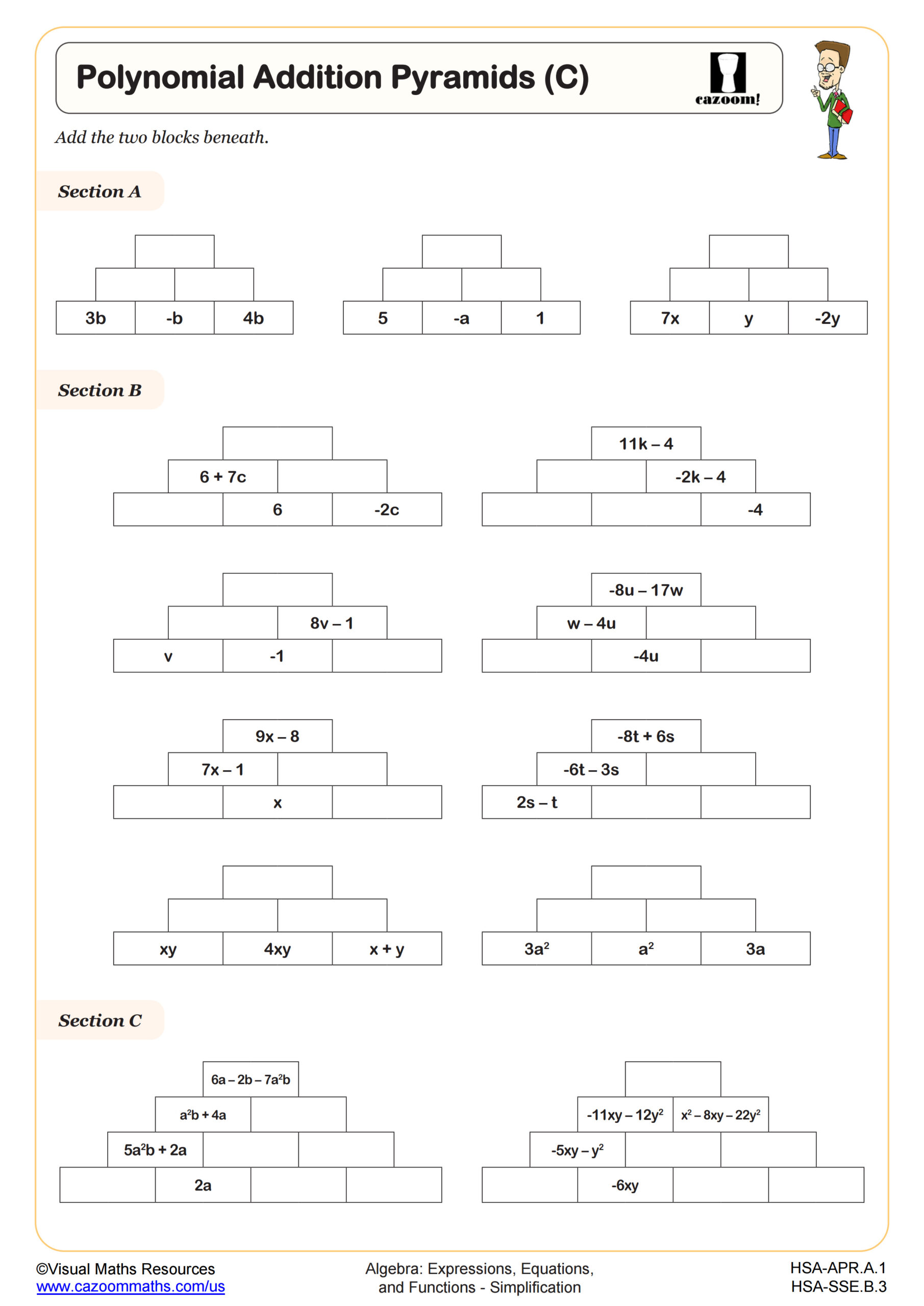
Polynomial Multiplication Grids
Proving Equivalent Expressions

Simplify Algebraic Fractions (A)
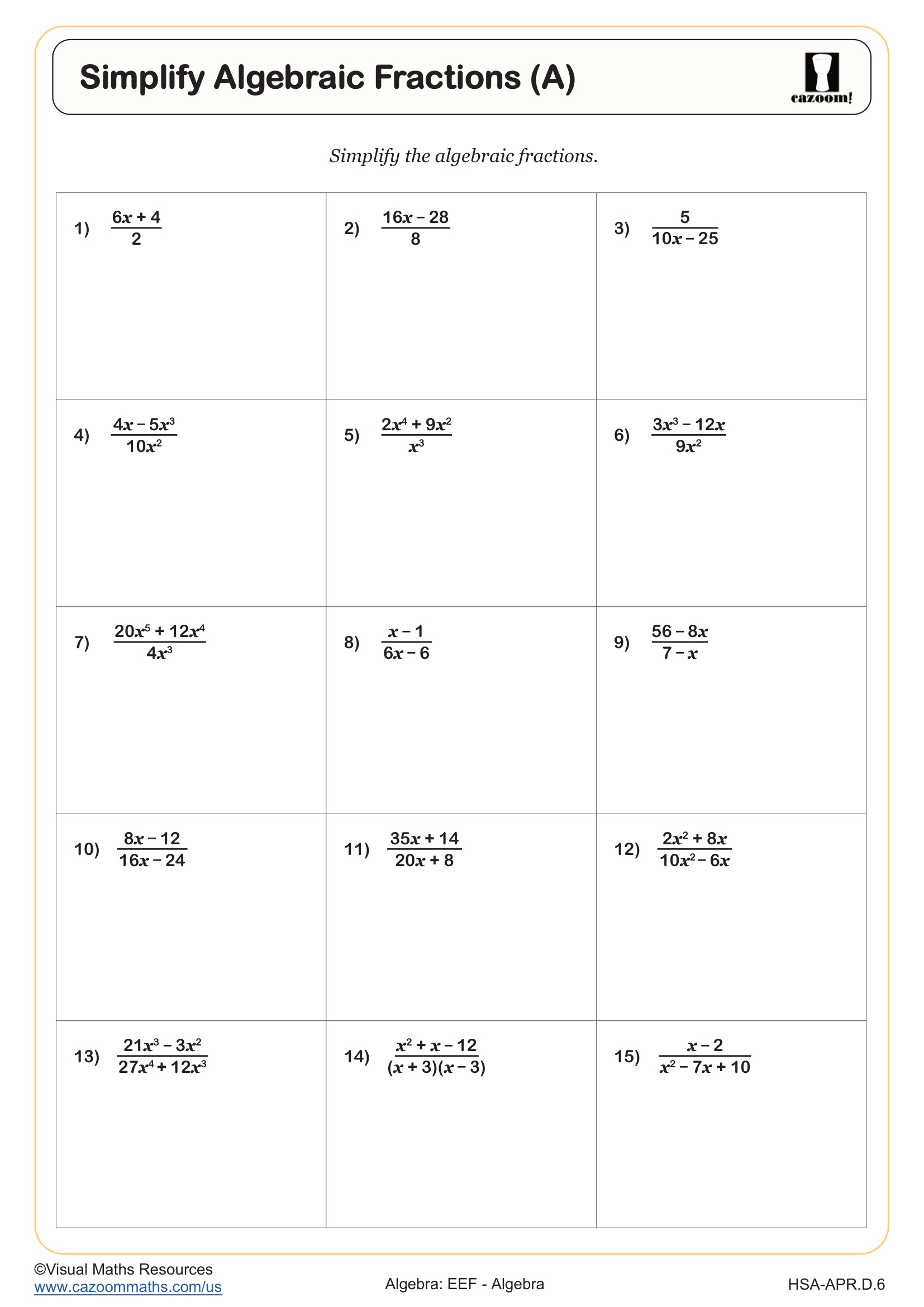
Simplify Algebraic Fractions (B)

Simplifying Expressions by Combining Like Terms

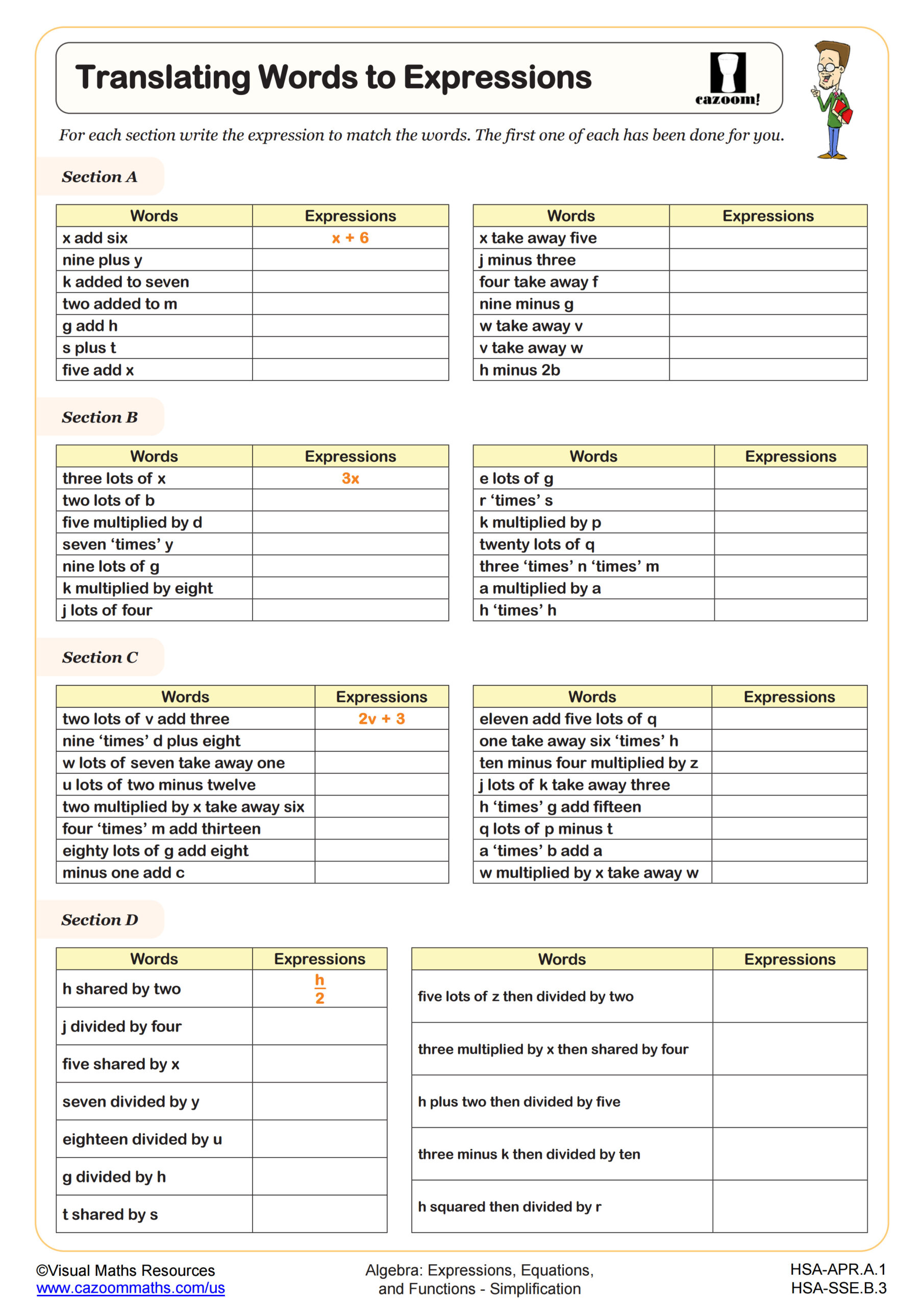
Translating Words to Expressions
Writing Expressions: Thinking of a Number

What Does Simplification Cover in Algebra I?
Simplification in Algebra I focuses on rewriting algebraic expressions in their simplest form by combining like terms, applying the distributive property, and performing operations with polynomials. Students learn to recognize which terms can be combined, how to distribute coefficients correctly across parentheses, and how to add, subtract, and multiply polynomial expressions while maintaining mathematical equivalence.
Teachers frequently notice students making sign errors when distributing negative coefficients, especially with expressions like -3(2x - 5). Many students correctly get -6x but then write -15 instead of +15 because they forget that subtracting a negative creates a positive. Practice with varied coefficient signs helps students develop automatic accuracy with these operations before moving into equation solving.
How Does Simplification Appear on the SAT and State Assessments?
Standardized tests like the SAT and ACT embed simplification within multi-step problems rather than asking students to simply "simplify this expression." Students might need to simplify algebraic expressions when solving equations, working with functions, or setting up word problems. The tests assess whether students can accurately manipulate expressions as part of broader problem-solving contexts, often within calculator and no-calculator sections.
Students lose points when they rush through simplification steps and fail to combine all like terms before attempting to solve. Another common error on timed assessments involves incorrectly distributing when expressions contain subtraction, leading to wrong answers even when students understand the underlying concept. State assessments often include constructed-response items where work must be shown, making clean simplification steps critical for partial credit.
Why Is the Distributive Property Central to Simplification?
The distributive property allows students to multiply a single term across terms inside parentheses, transforming expressions like 4(3x + 2) into 12x + 8. This property is fundamental because it appears in virtually every algebraic manipulation, from expanding expressions to factoring and solving equations. The grid method provides a visual approach that helps students see how each term multiplies, reducing errors and building conceptual understanding alongside procedural skill.
Engineers and scientists apply the distributive property when working with formulas and equations. For example, calculating the total cost of purchasing multiple items at different prices requires distributing quantities across unit prices. In physics, the distributive property appears when analyzing forces acting on objects or when simplifying formulas for motion. College-bound students benefit from automatic fluency with this property since it underlies calculus operations and linear algebra concepts they'll encounter in STEM courses.
How Can Teachers Use These Algebra I Simplification Worksheets?
These worksheets provide scaffolded practice starting with basic like-term identification and progressing through multi-step polynomial operations. The variety of formats—including addition pyramids where students work backward to find missing terms and perimeter problems that connect algebra to geometry—keeps practice engaging while building the same core skills. Answer keys allow students to self-check during independent work or homework, promoting metacognition about their own error patterns.
Many teachers use these worksheets for differentiated small-group instruction, assigning simpler formats to students who need reinforcement while giving more complex polynomial multiplication problems to students ready for additional challenge. The worksheets work well as warm-ups before lessons on equation solving, as targeted intervention for students who make simplification errors on tests, or as review material before unit assessments. Teachers also pair students to work through problems collaboratively, with one simplifying while the other checks against the answer key.