Algebra II Solving Equations Worksheets
What Equation-Solving Skills Do Algebra II Students Practice?
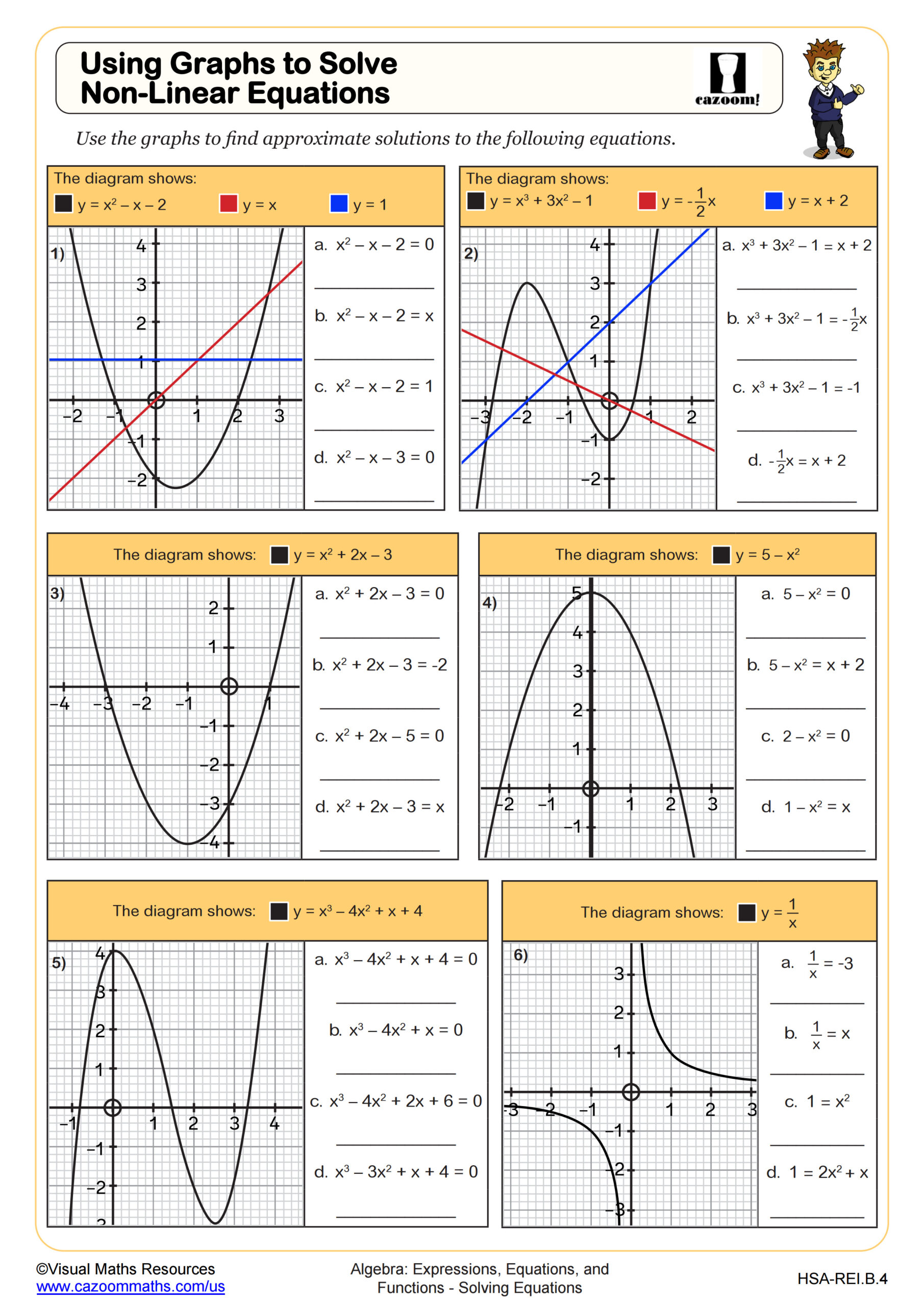
Algebra II students move beyond linear equations to solve quadratic systems, interpret graphical solutions to non-linear equations, and apply multiple solution methods to increasingly complex problems. These worksheets focus on using graphs to identify solutions where algebraic methods become cumbersome and solving systems where at least one equation is quadratic. Students connect algebraic and graphical representations of the same mathematical relationships, a skill the Common Core State Standards emphasize throughout high school.
A common error occurs when students identify intersection points on a graph but then incorrectly report only the x-coordinate as "the solution" rather than the complete ordered pair. Teachers frequently reinforce that solutions to systems of equations represent points where both equations are simultaneously satisfied, requiring both coordinates. This distinction becomes particularly important when systems have two solutions, as with many quadratic systems.
How Does Solving Equations Appear on the SAT and ACT?
Both the SAT and ACT regularly include questions where students must solve systems involving quadratic equations or interpret graphs to determine solution sets. The SAT calculator section often presents graphs of two functions and asks students to identify the number of solutions or the approximate coordinates of intersection points. Students must demonstrate understanding of what a solution represents geometrically and algebraically, not just follow memorized procedures.
Students lose points when they fail to check whether their algebraic solutions make sense within the given context or when graphical approximations are required. Test questions frequently include distractors based on common errors like substituting into only one equation or misreading graph scales. Many students also struggle with questions asking for the number of solutions without requiring calculation of exact values, a question type that rewards strong conceptual understanding.
What Does Solving Systems of Quadratic Equations Involve?
Solving systems where one or both equations are quadratic requires students to apply substitution or elimination methods while managing squared terms and potential multiple solutions. Students typically solve one equation for a variable, substitute into the second equation, and then solve the resulting quadratic equation using factoring, completing the square, or the quadratic formula. This process can yield zero, one, or two solution pairs, depending on whether the graphs of the two equations intersect.
These skills connect directly to physics applications where students model projectile motion or optimize design constraints. For example, determining where two objects in parabolic flight paths might collide requires solving a system of quadratic equations. Engineers use similar techniques when analyzing stress curves or optimizing materials that follow non-linear relationships, making this topic relevant for STEM-focused students planning technical coursework in college.
How Can Teachers Use These Algebra II Worksheets Effectively?
These worksheets provide structured practice that bridges conceptual understanding and procedural skill, with graphical and algebraic approaches presented together to reinforce connections. The included answer keys show complete solution steps, allowing students to identify where their process diverged from correct methods. Teachers find these particularly useful for helping students develop the habit of verifying solutions both algebraically and graphically, a strategy that catches many careless errors.
Many teachers assign these worksheets as targeted practice before unit assessments or use them during intervention sessions with students who struggled on previous tests. The graphical emphasis makes them effective for paired work, where one student can describe what they see on the graph while their partner works through the algebra. They also work well as SAT/ACT prep materials since the problem types mirror testing formats, giving college-bound students exposure to the multi-representational thinking standardized tests reward.