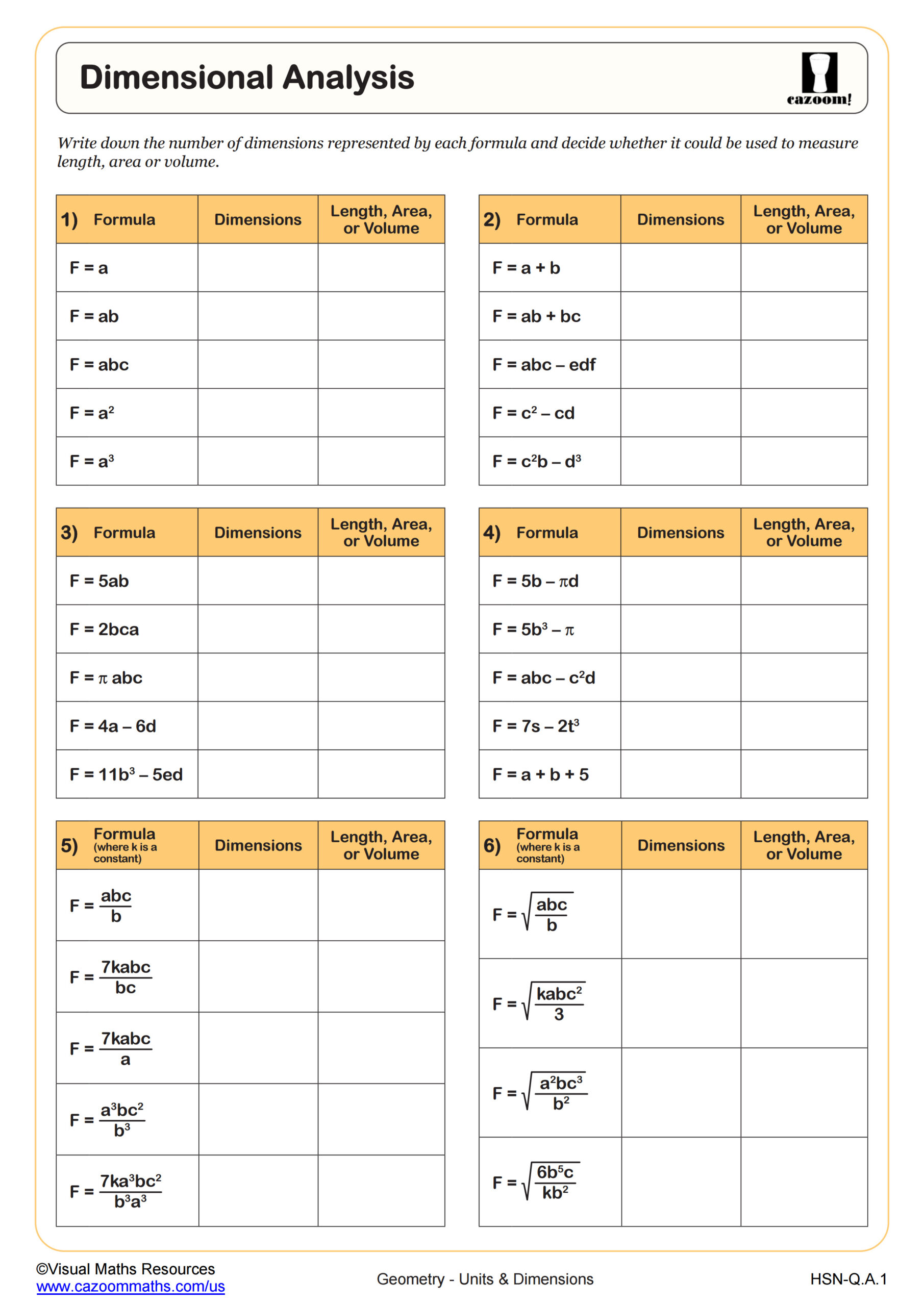
Algebra II Units and Dimensions Worksheets
What Do Algebra II Students Learn About Units and Dimensions?
In Algebra II, students extend their understanding of dimensional analysis beyond simple conversions to tackle problems involving compound units like miles per hour, grams per milliliter, or dollars per square foot. They learn to set up conversion chains where multiple factors must be applied sequentially, canceling units systematically until reaching the target measurement. This topic reinforces ratio and proportion concepts while introducing the mathematical rigor needed for science courses.
A common error occurs when students write conversion factors upside down, placing the unit they want to eliminate in the numerator instead of the denominator. Teachers often address this by having students physically cross out units as they cancel, making the pattern visible. Students also practice dimensional consistency, verifying that formulas and calculations produce appropriate units for the context, a skill that becomes invaluable when checking work in physics and chemistry.
How Are Units and Dimensions Tested on the SAT and ACT?
Standardized tests embed dimensional analysis within word problems across multiple content areas, particularly in science-based scenarios. The SAT and ACT expect students to convert units correctly when solving rate problems, interpret graphs with labeled axes in different units, and recognize when unit conversion is necessary to answer a question. These problems test whether students can identify relevant conversion factors and apply them accurately under time pressure.
Students lose points when they fail to convert all measurements to consistent units before calculating, such as mixing feet and yards in a geometry problem or using minutes and hours interchangeably in rate calculations. Another frequent mistake involves misreading compound units, treating square feet as linear feet or confusing cubic measurements with area measurements. State assessments increasingly include multi-step problems requiring two or three conversions, testing both conceptual understanding and computational accuracy.
What Is the Factor-Label Method and Why Does It Matter?
The factor-label method, also called unit analysis or dimensional analysis, provides a systematic approach for converting measurements by multiplying by carefully chosen fractions that equal one. Students write conversion factors as fractions, positioning units so unwanted dimensions cancel algebraically while desired units remain. This method reduces errors because the units themselves guide the problem setup, and students can verify correctness before calculating by checking that only target units survive the cancellation process.
This technique appears constantly in STEM fields, from chemistry stoichiometry problems converting moles to grams to physics calculations involving velocity, acceleration, and force. Engineers use dimensional analysis to verify that complex formulas produce sensible results, catching errors before expensive prototypes are built. Students preparing for AP Chemistry and AP Physics benefit significantly from mastering this method early, as those courses assume fluency with multi-step unit conversions and dimensional reasoning when solving quantitative problems.
How Can Teachers Use These Worksheets in Algebra II Classrooms?
These worksheets provide structured practice in dimensional analysis, starting with straightforward single-step conversions and progressing to problems requiring multiple conversion factors. The answer keys show complete work, including how conversion factors are set up and how units cancel at each stage, giving students a model for organizing their own solutions. This transparency helps students self-diagnose errors in their setup rather than just checking final numerical answers.
Teachers find these worksheets effective for small-group work where students can discuss which conversion factors to apply and in what order. They work well as targeted review before unit tests or as intervention materials for students struggling with unit conversions in concurrent science courses. Many teachers assign selected problems as warm-ups before chemistry or physics lessons, reinforcing that dimensional analysis is a cross-curricular skill. The worksheets also serve as practical test prep, since standardized assessments frequently embed unit conversion within applied problems.