Circle Worksheets and Answers
Constructing an Easter Egg
Grades: 4th Grade, Geometry, IM 1

Easter Egg Dimension
Grades: 4th Grade, Geometry, IM 1

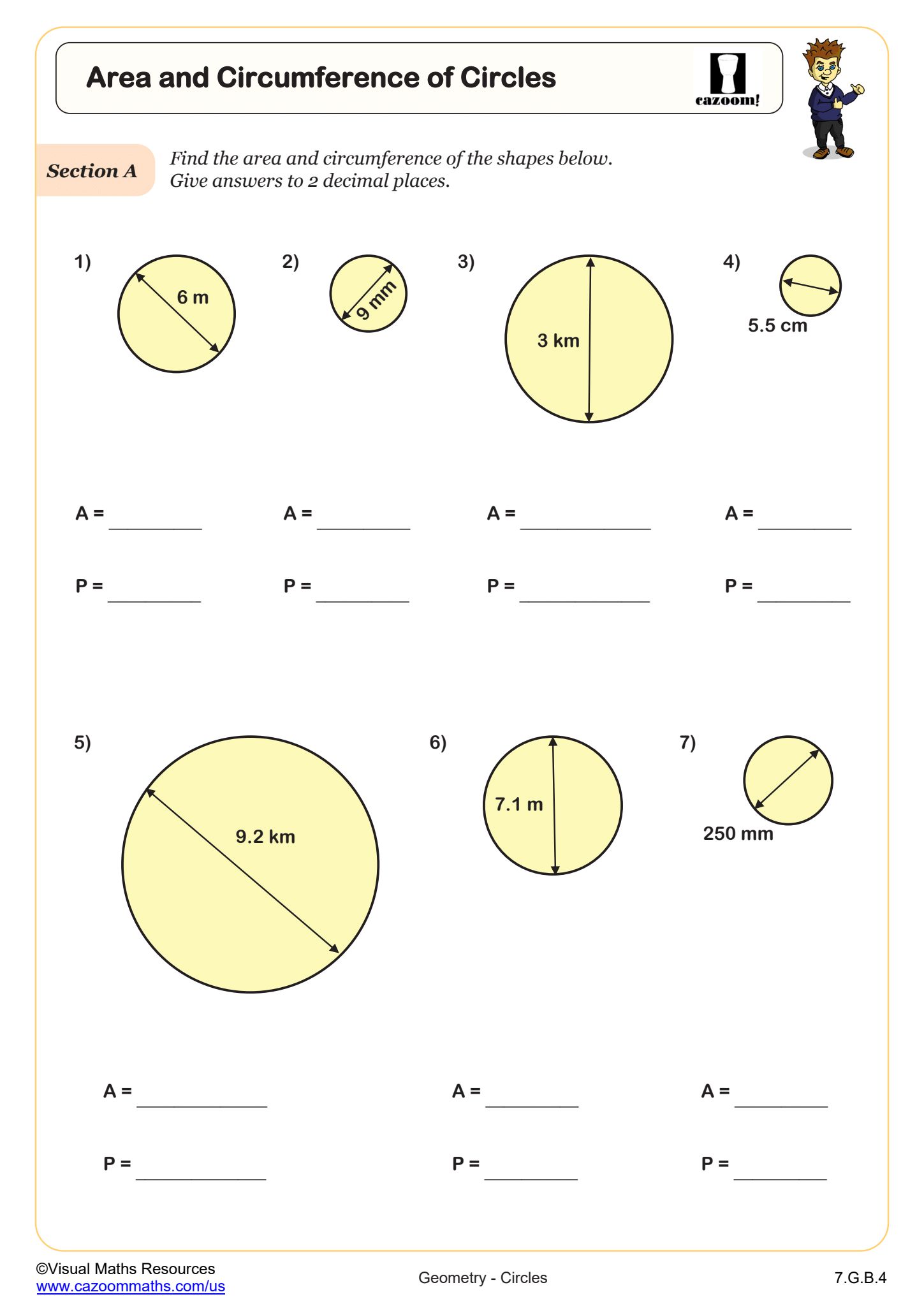
Area and Circumference of Circles
Grades: 7th Grade
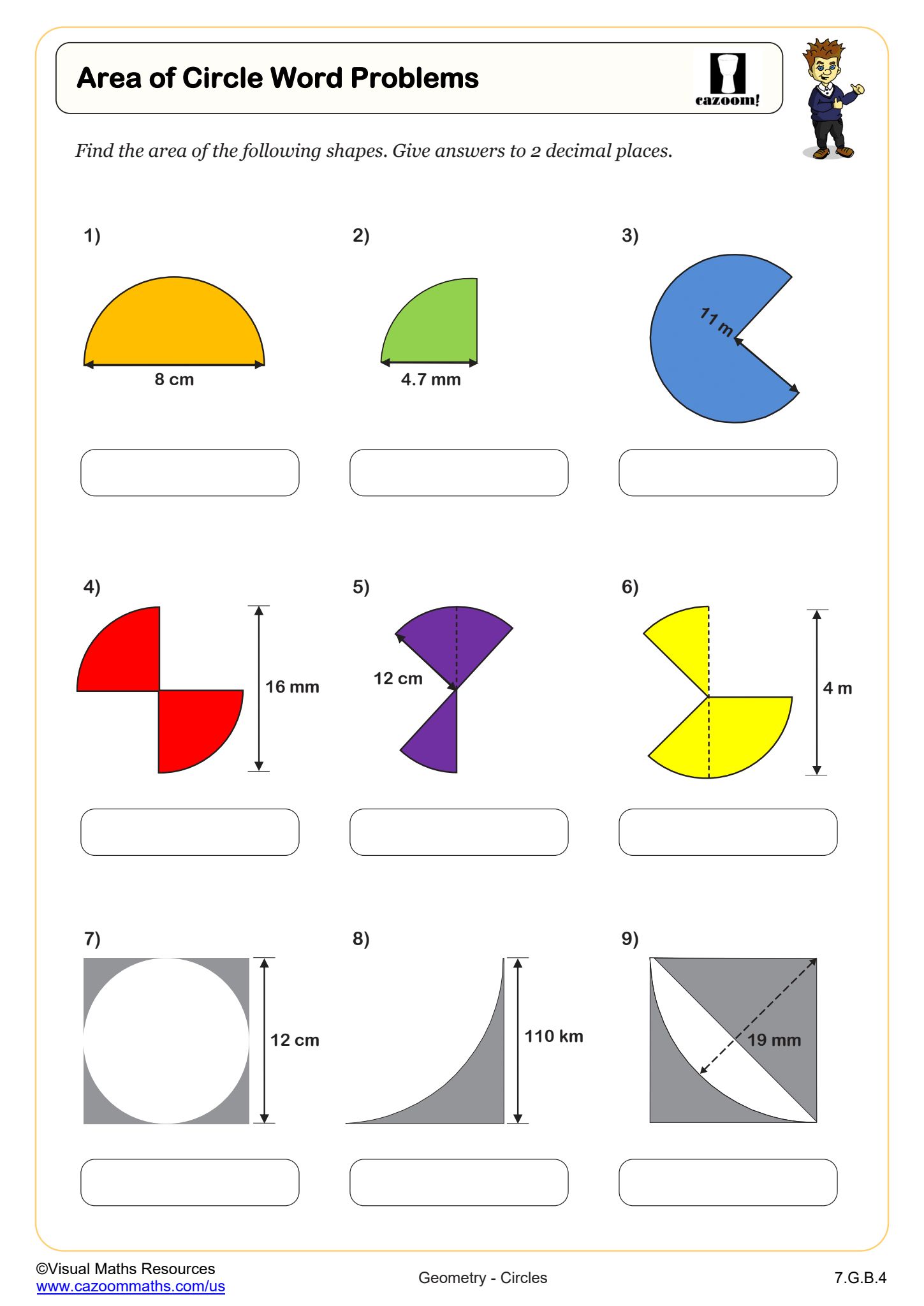
Area of Circle Word Problems
Grades: 7th Grade
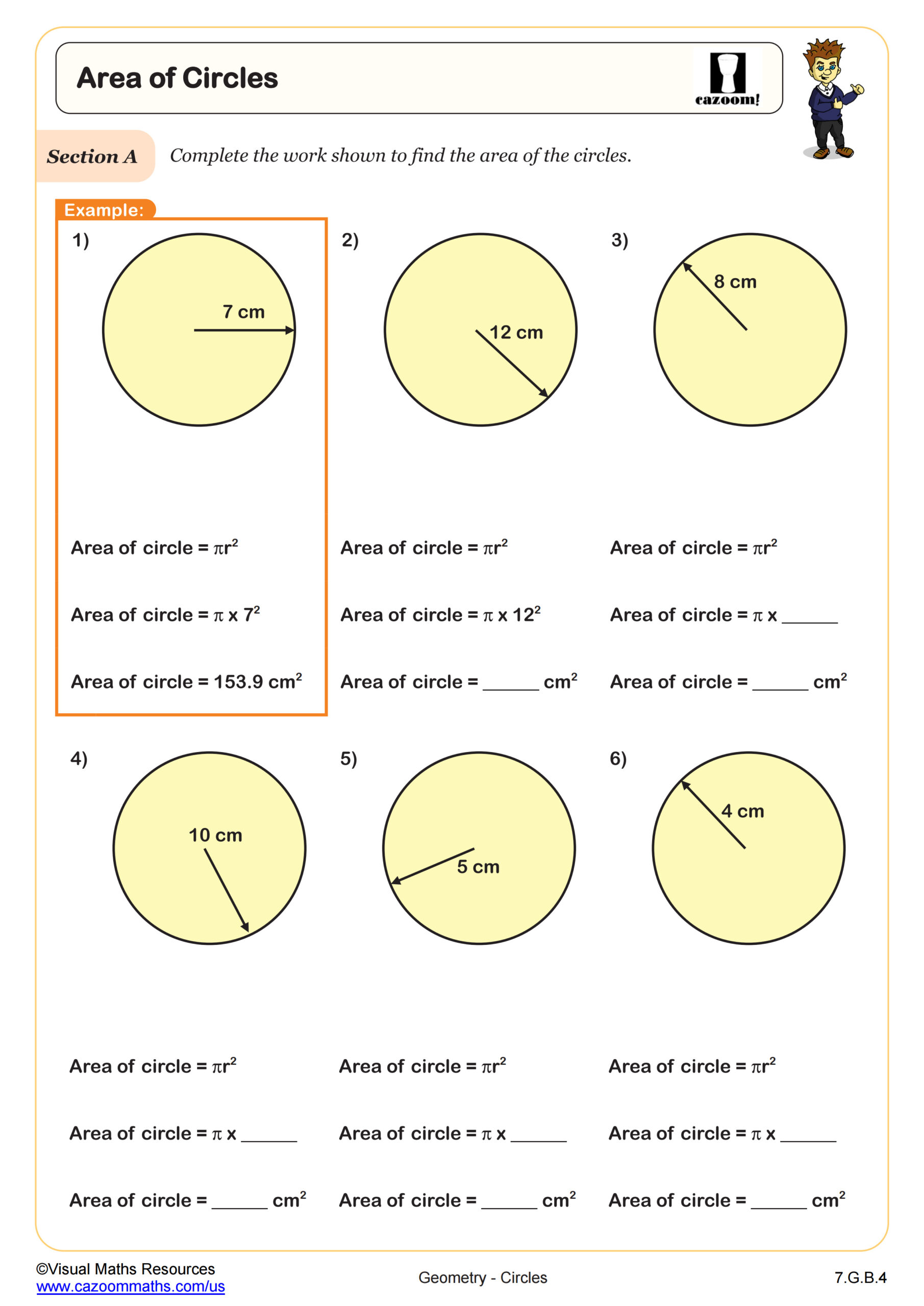
Area of Circles
Grades: 7th Grade
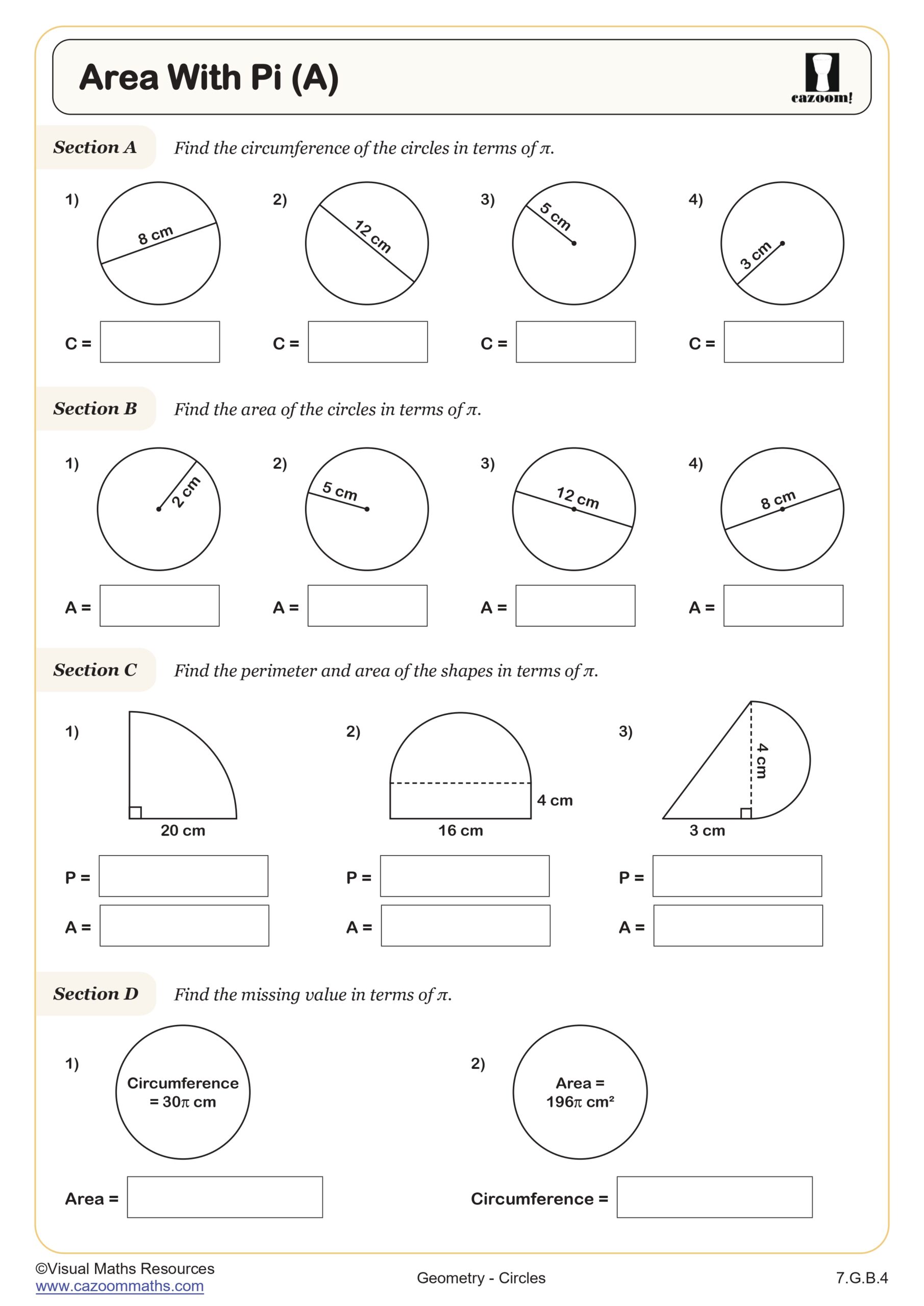
Area With Pi (A)
Grades: 7th Grade, Geometry, IM 2
Circle Theorems: Angle Notation
Grades: 7th Grade, Geometry
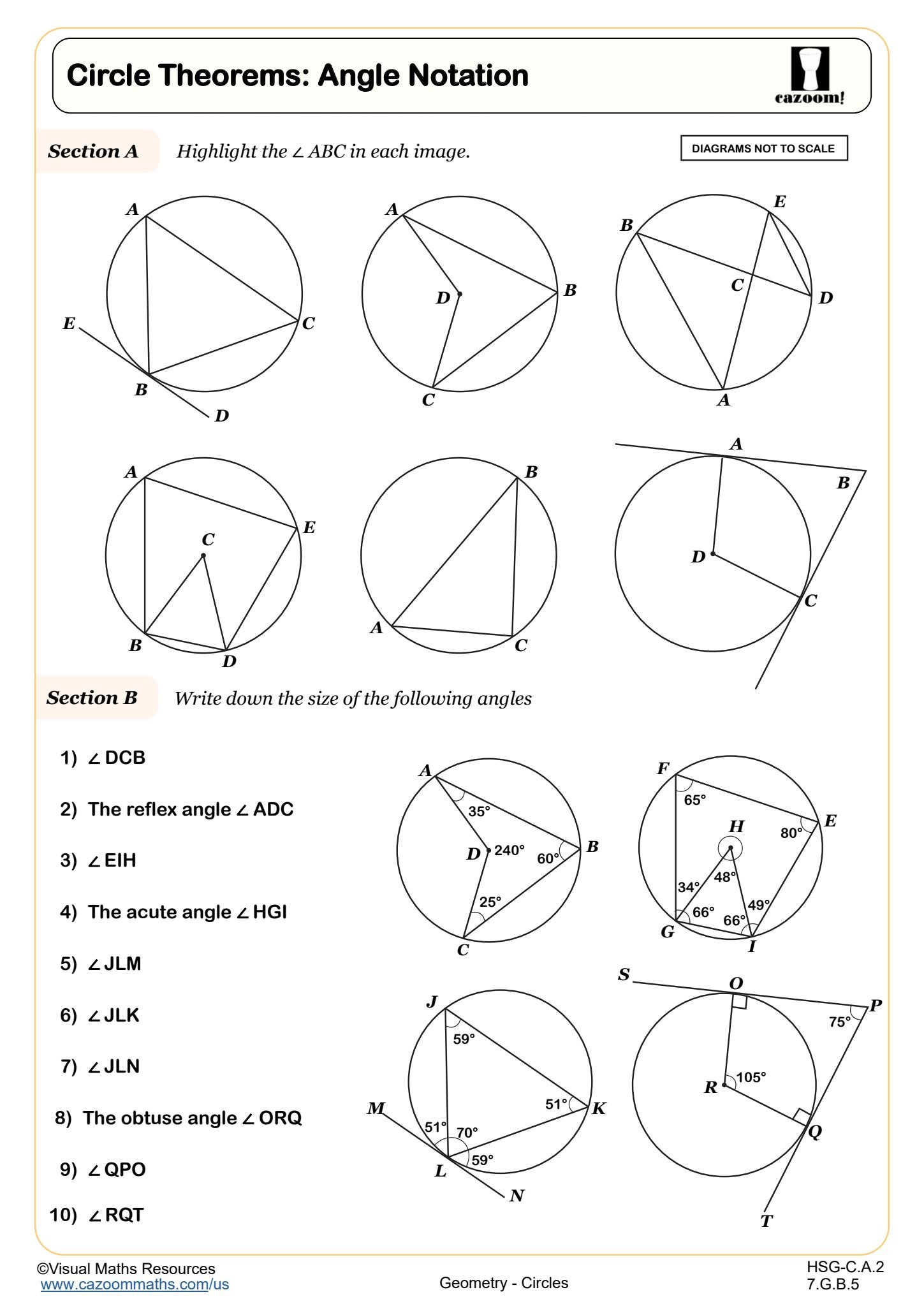
Circle Theorems: Cyclic Quadrilaterals
Grades: 7th Grade, Geometry
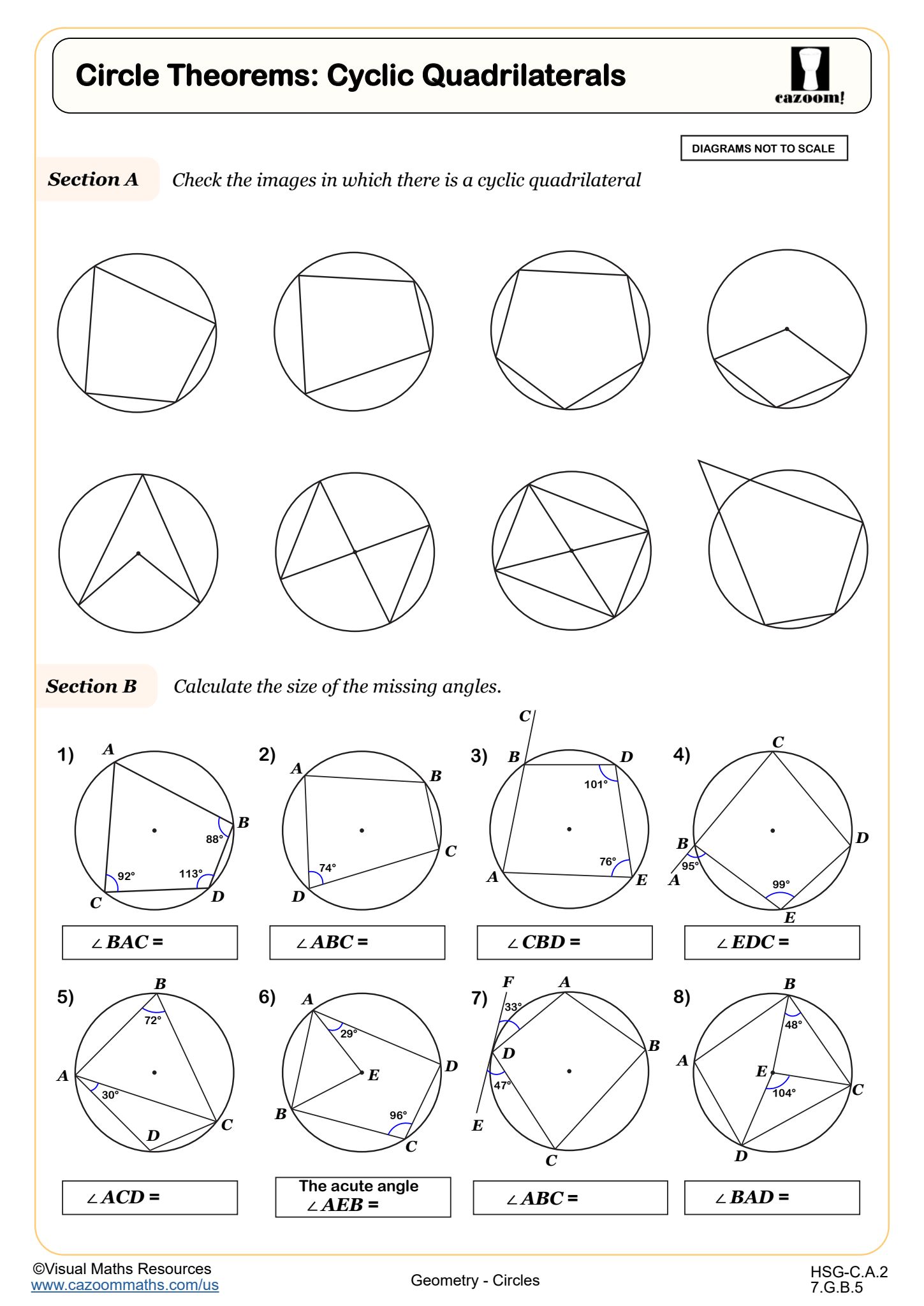
Circle Theorems: Triangles in Circles
Grades: 7th Grade, Geometry
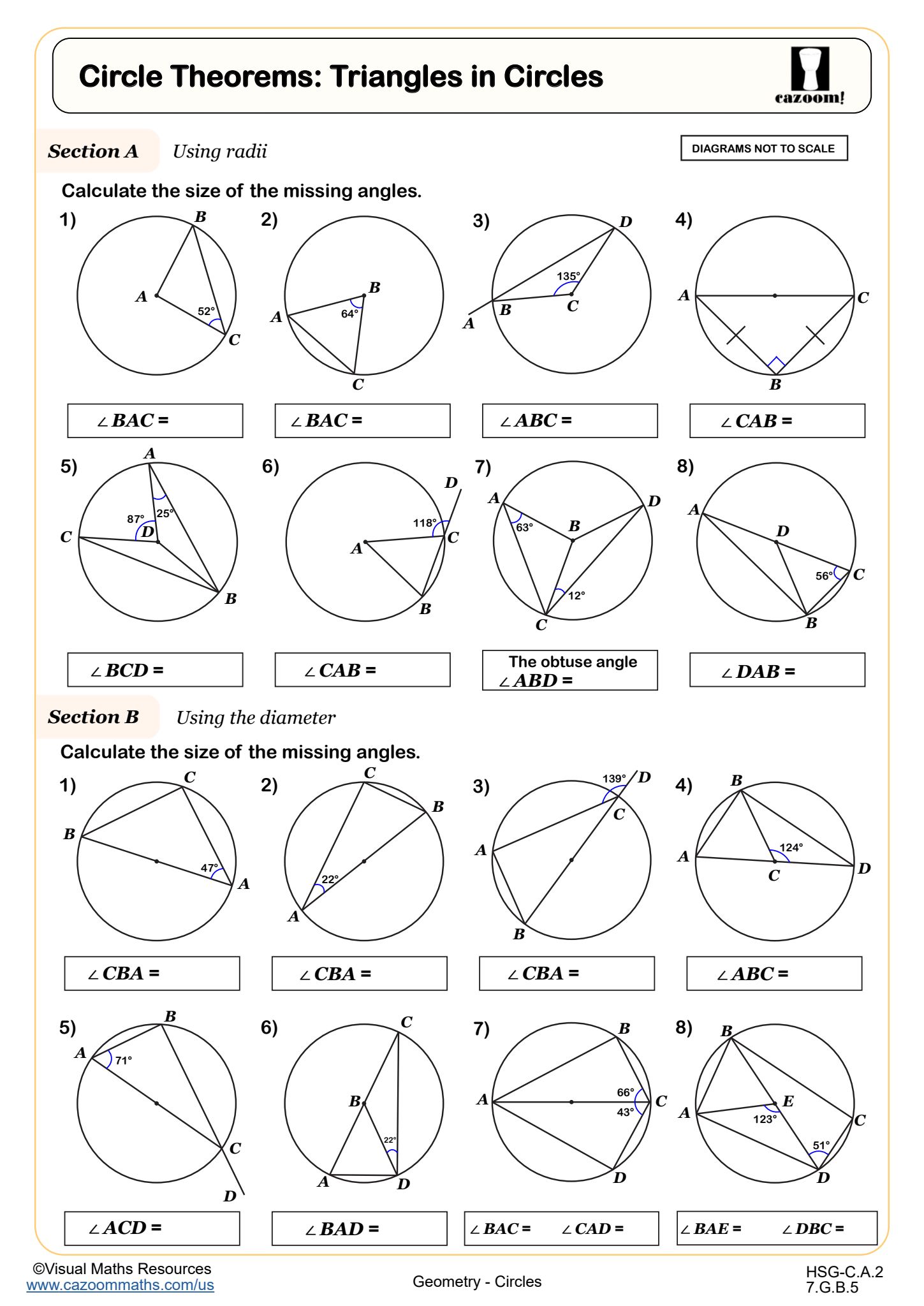
Circumference of Circles
Grades: 7th Grade
Finding the Radius and Diameter in Circles
Grades: 7th Grade

Area of Arc Lengths & Sectors
Grades: Geometry, IM 3

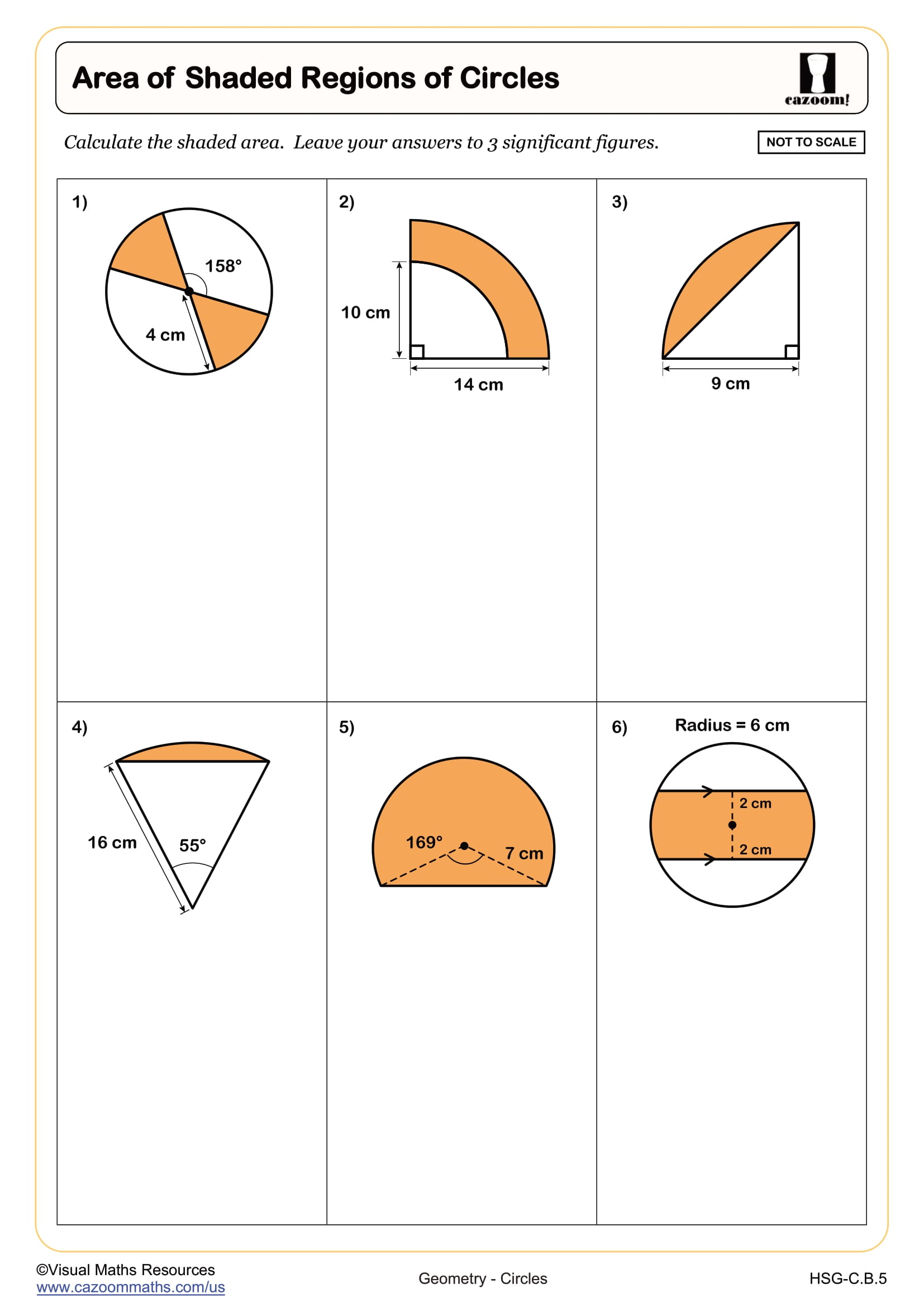
Area of Shaded Regions of Circles
Grades: Geometry, IM 3
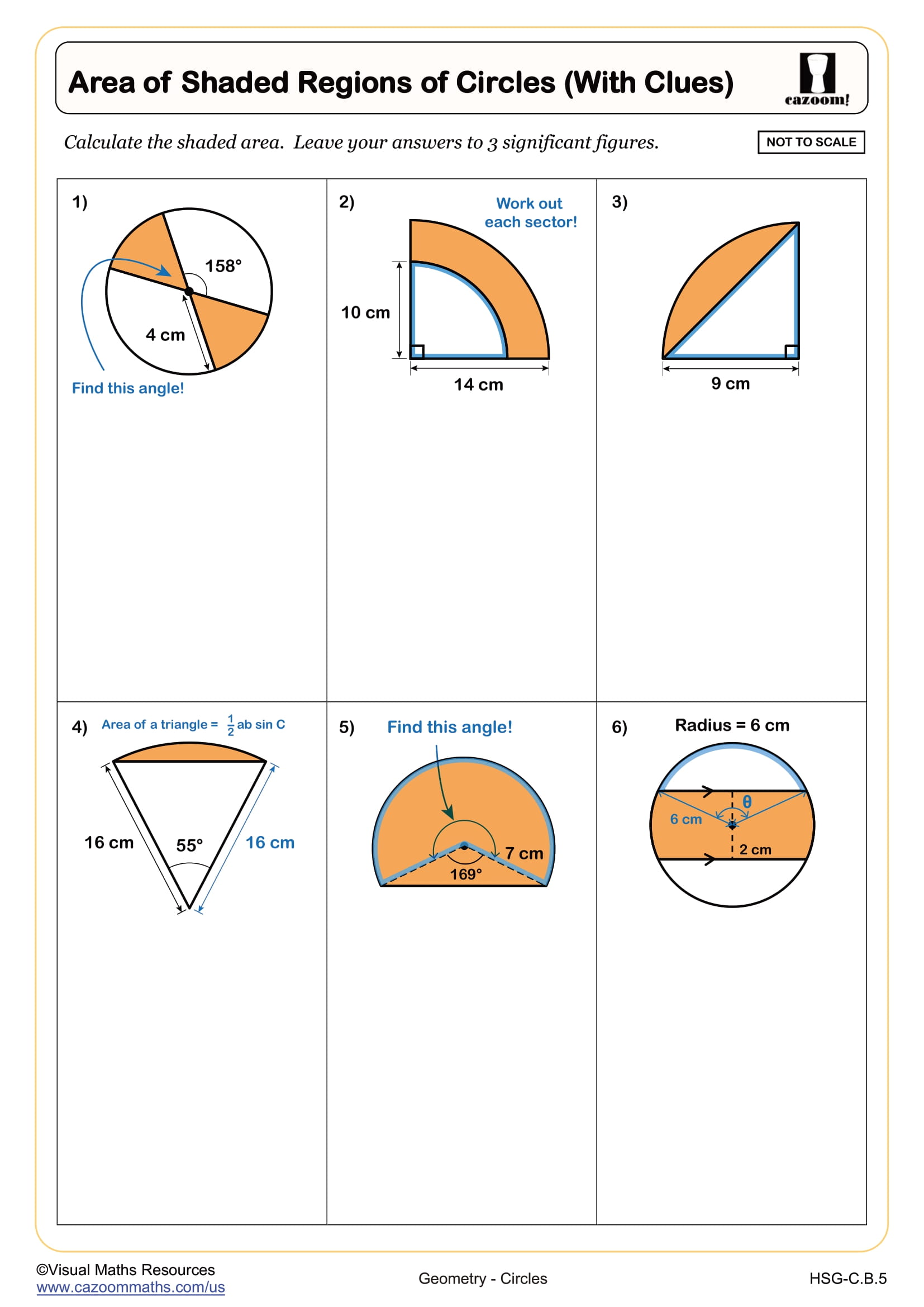
Area of Shaded Regions of Circles (with clues)
Grades: Geometry, IM 3
Circle Investigation - Discovering Pi
Grades: Geometry, IM 2

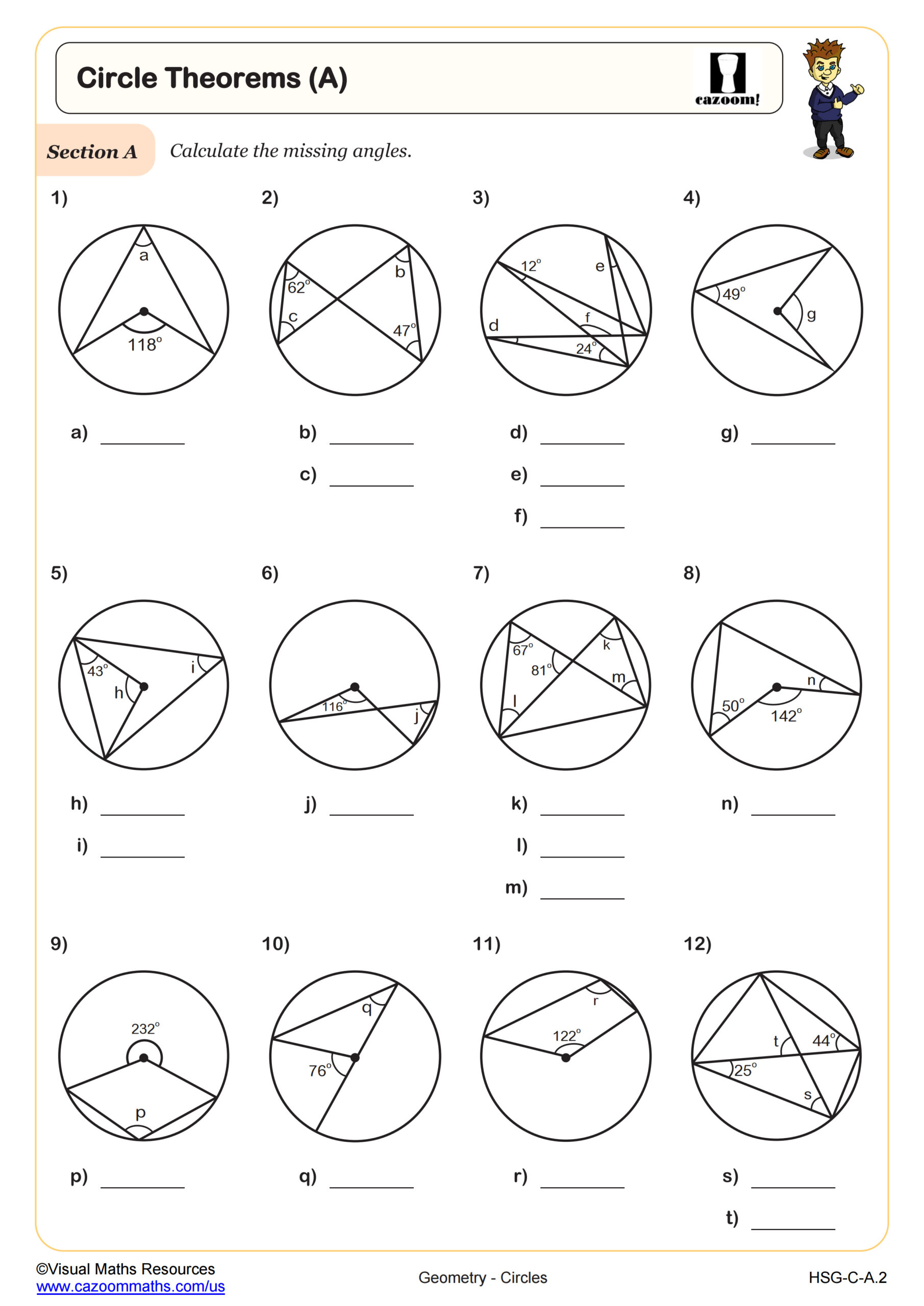
Circle Theorems (A)
Grades: Geometry, IM 3
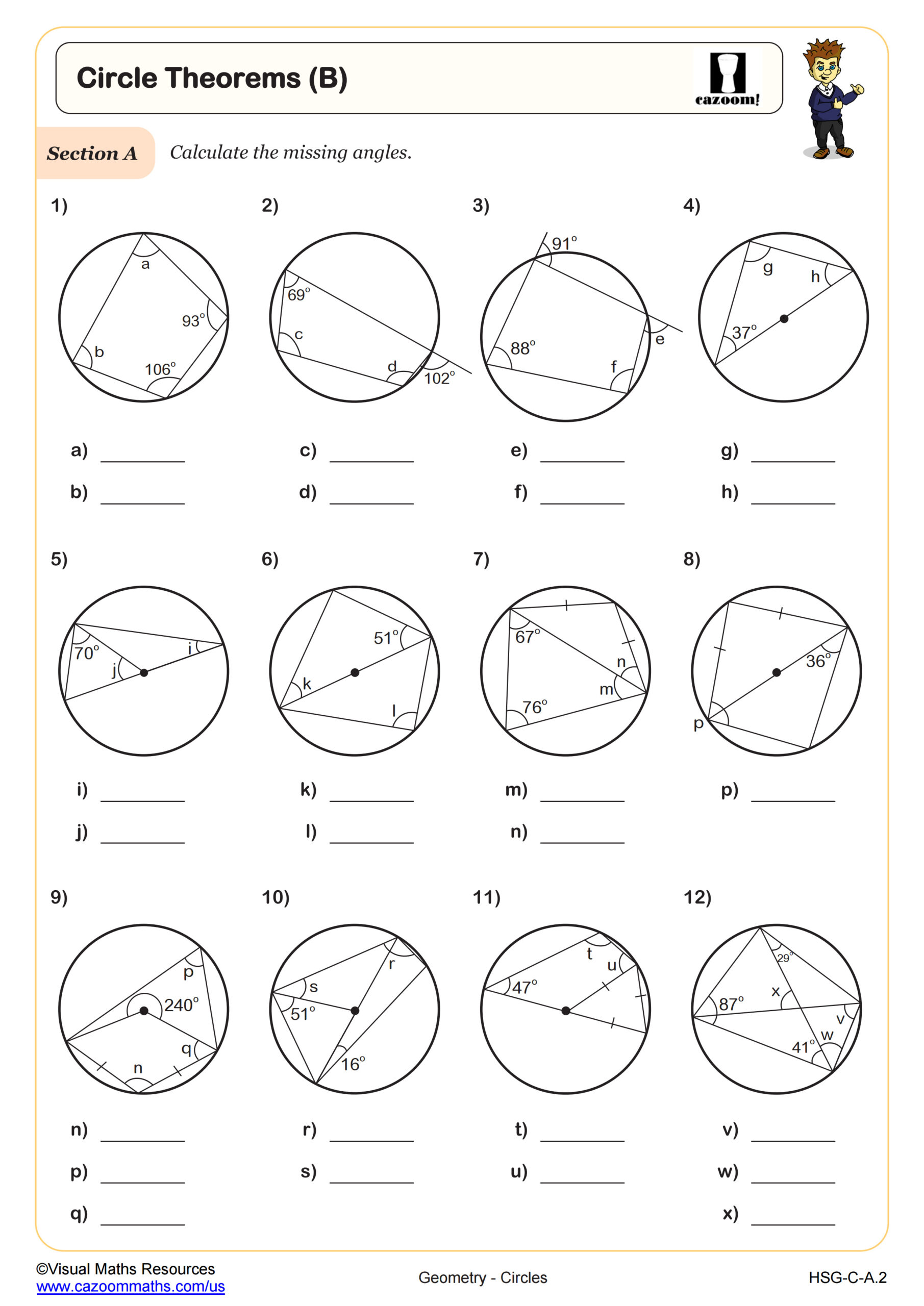
Circle Theorems (B)
Grades: Geometry, IM 3
Circle Theorems (C)
Grades: Geometry, IM 3
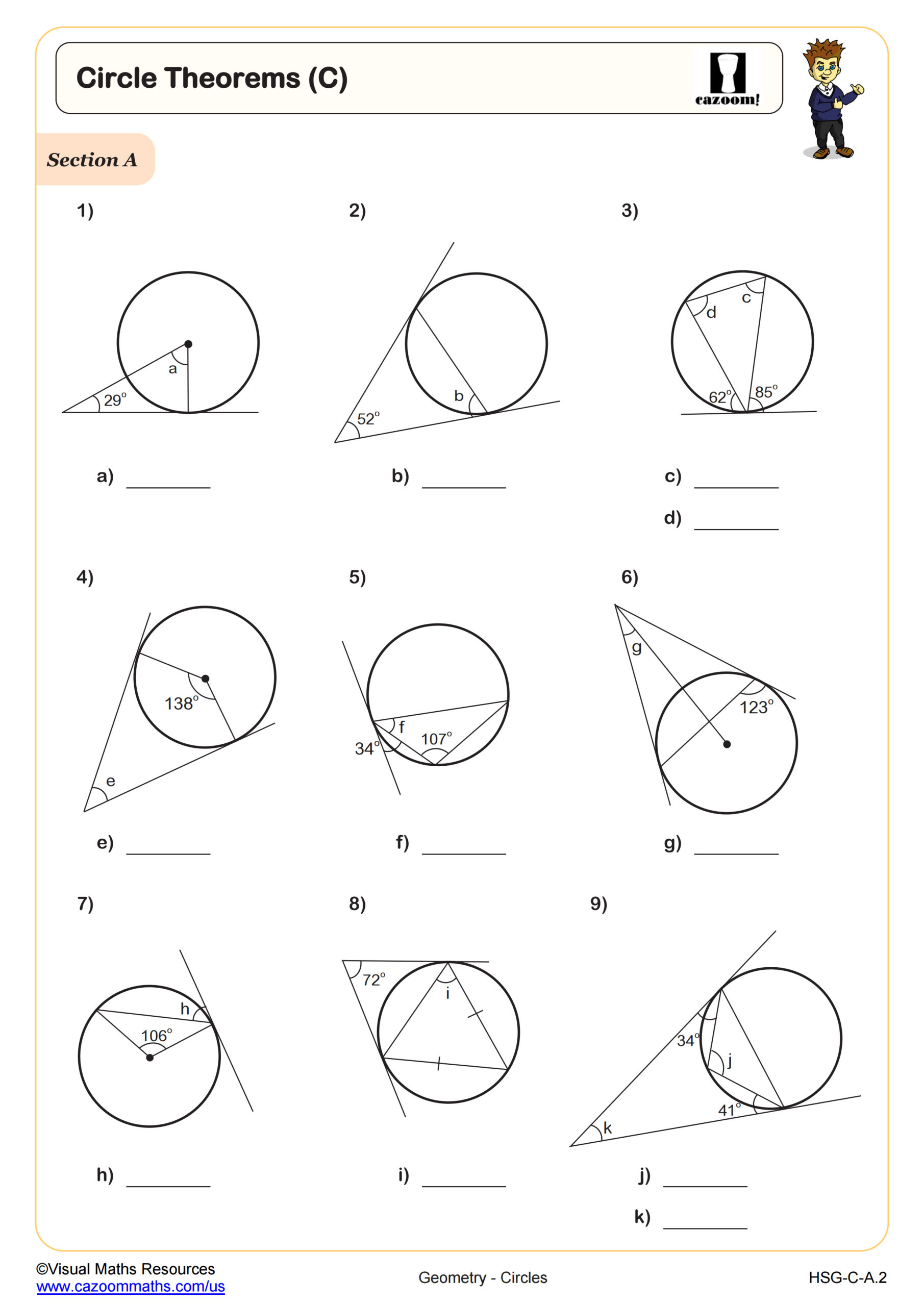
Constructing the Circle Theorems
Grades: Geometry, IM 3
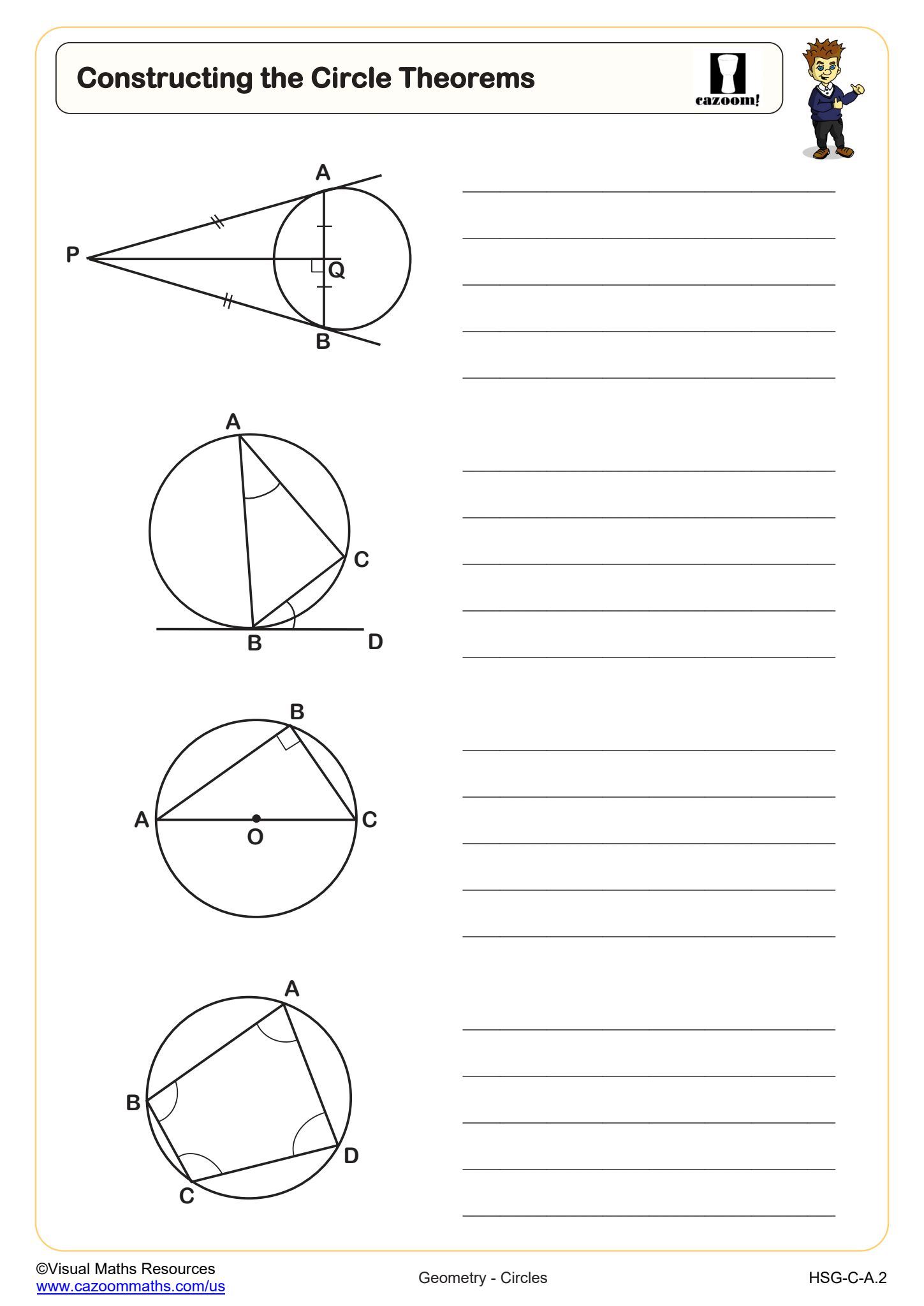
Equations of Circles
Grades: Geometry, IM 3
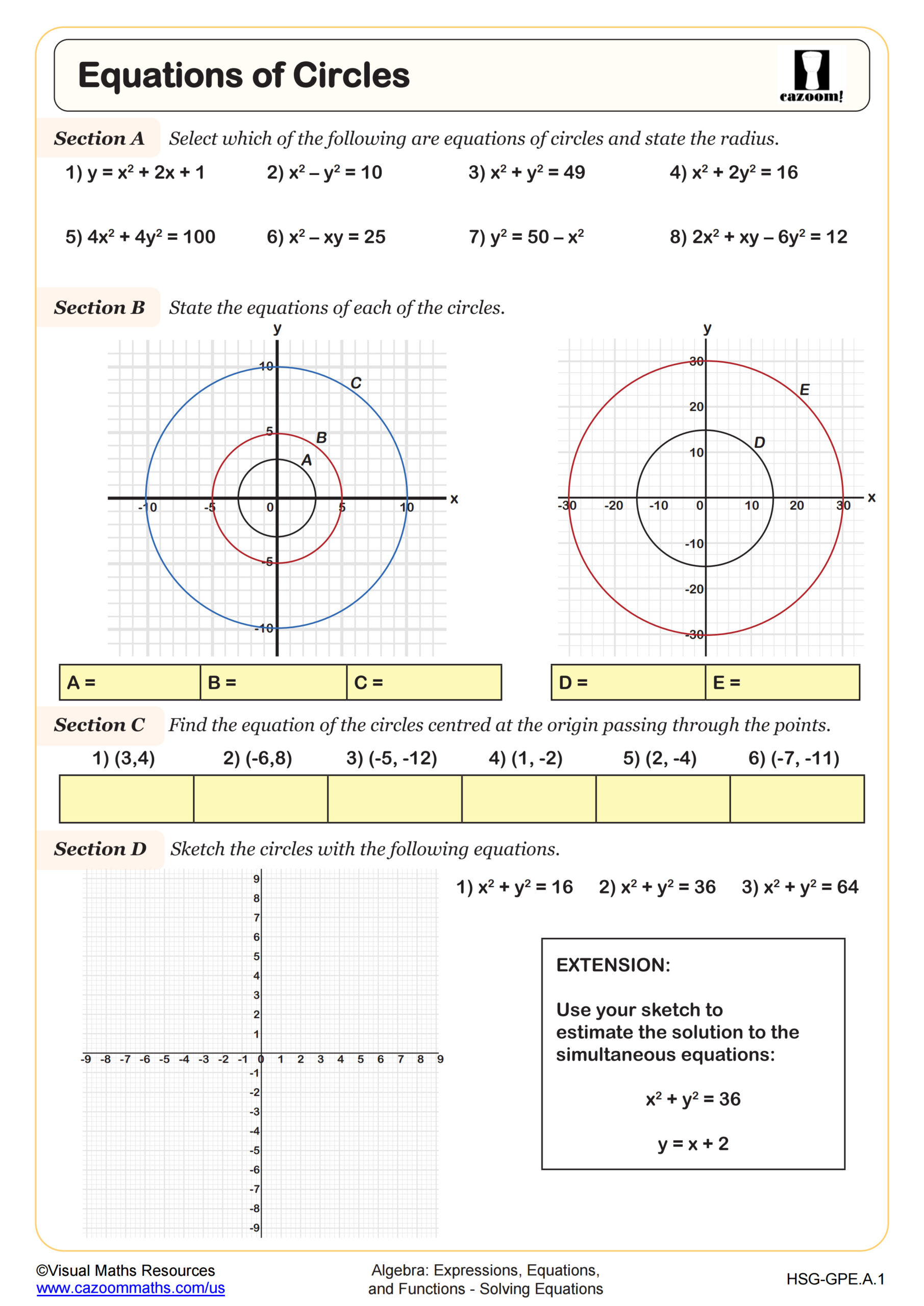
Equations of Lines Tangent to Circles
Grades: Geometry, IM 3
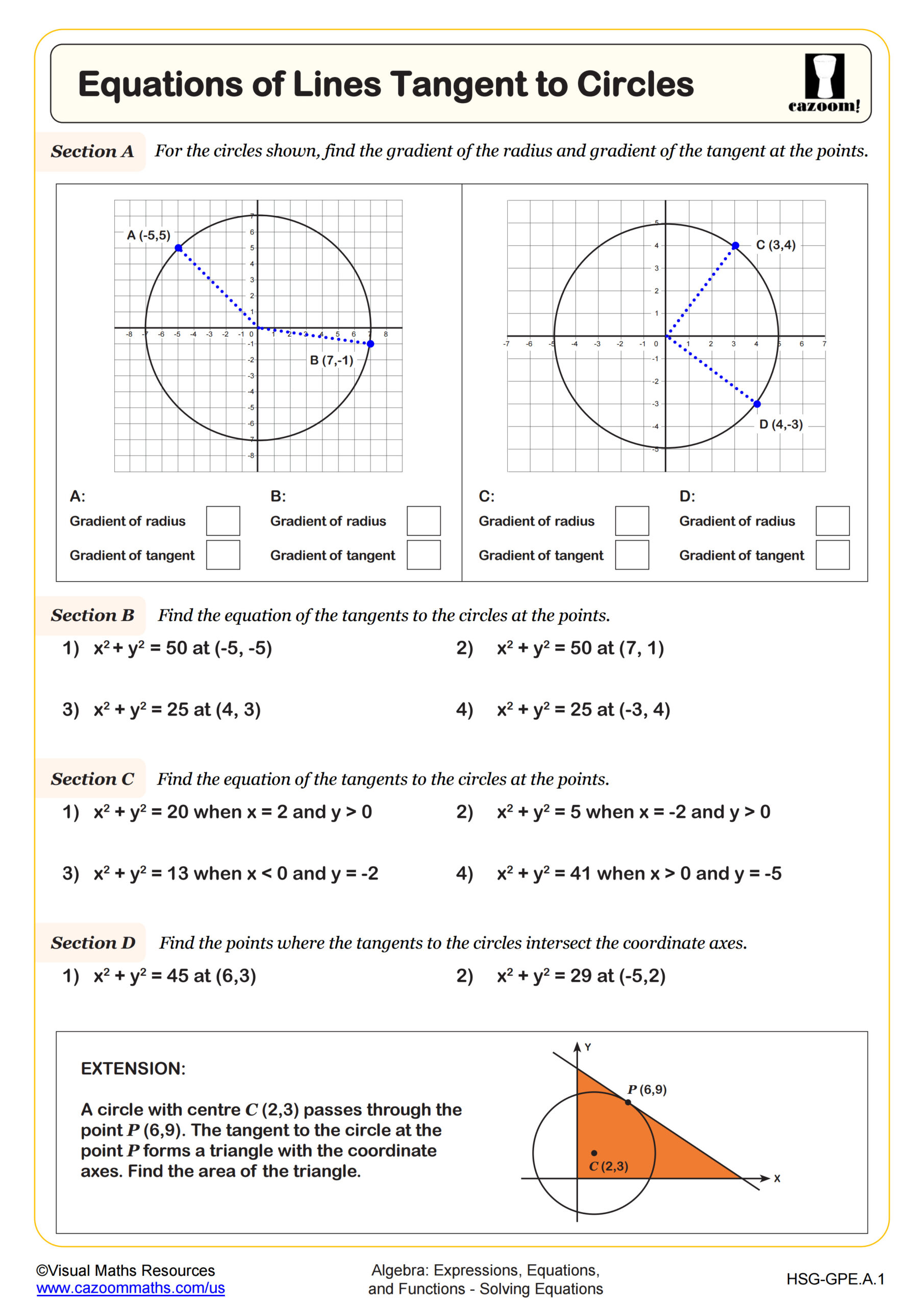
Formula for Area of Arc Length & Sectors
Grades: Geometry, IM 3
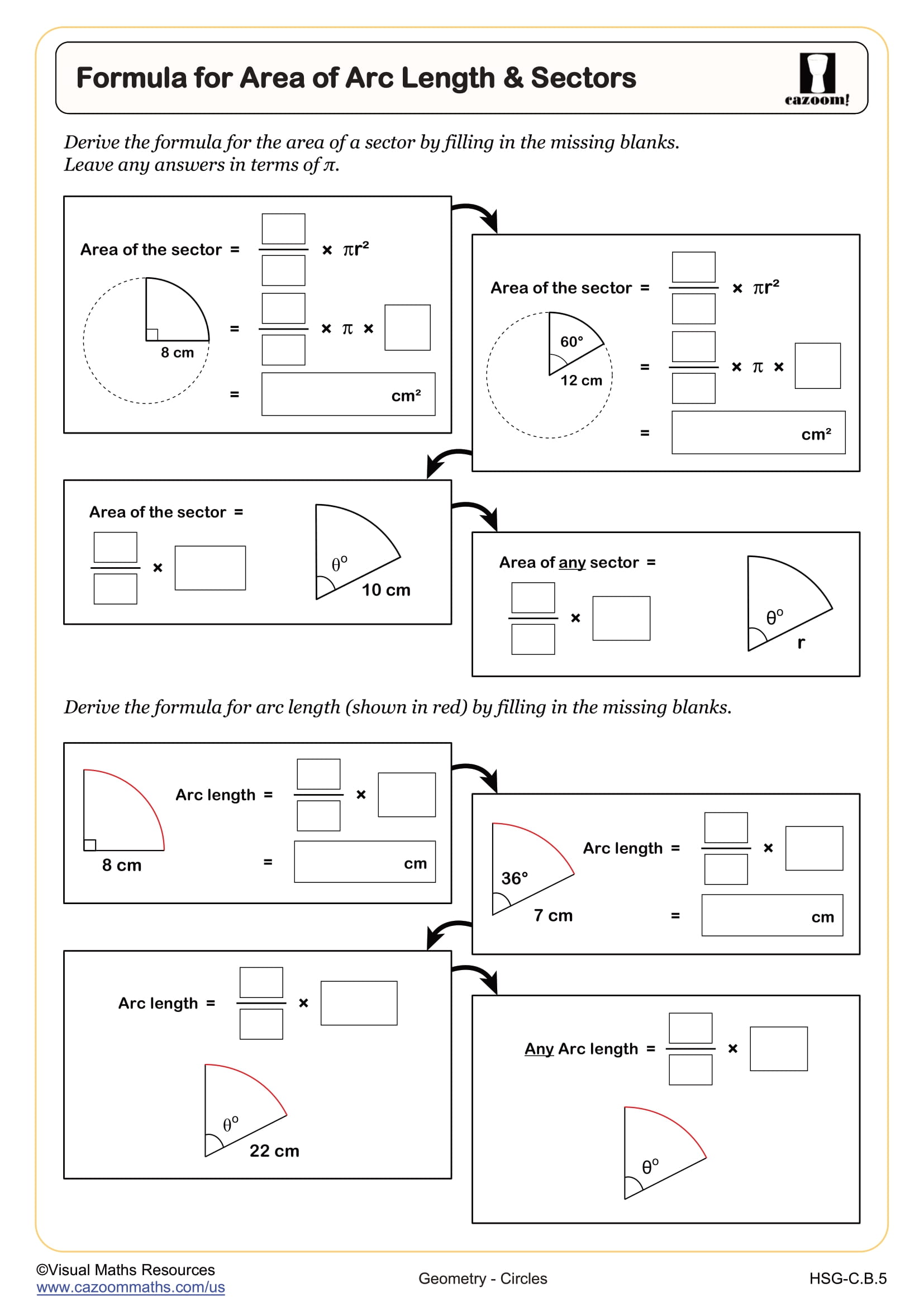
In Terms of Pi (B)
Grades: Geometry, IM 2

Pi (C)
Grades: Geometry, IM 2
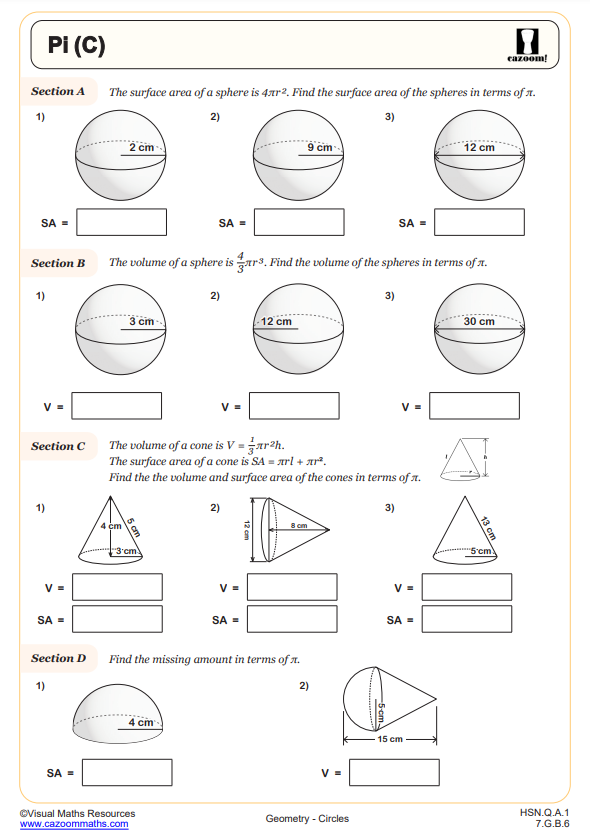
Proving Circle Theorems
Grades: Geometry, IM 2
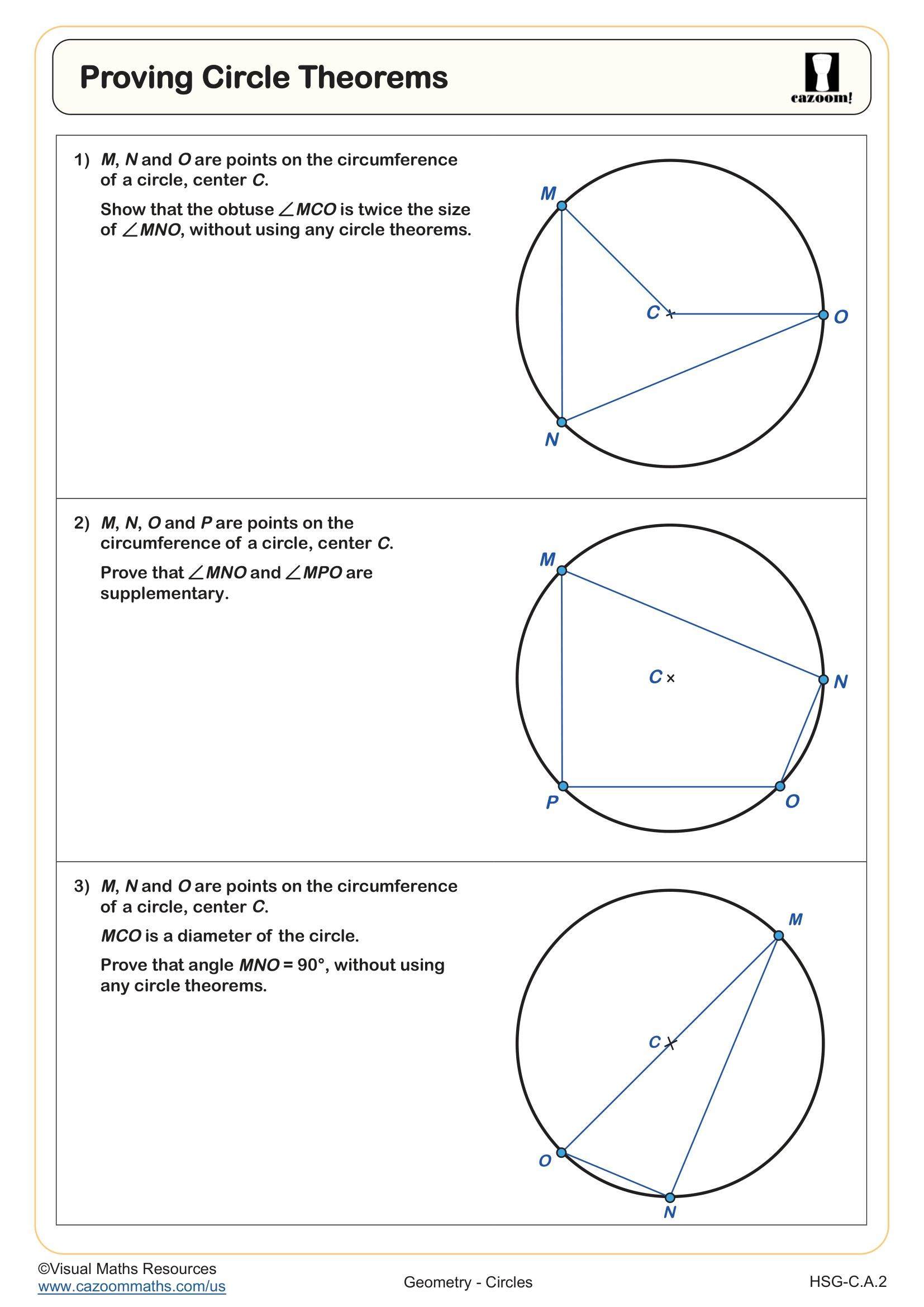
Proving Circle Theorems - Angle in a Semicircle
Grades: Geometry, IM 2
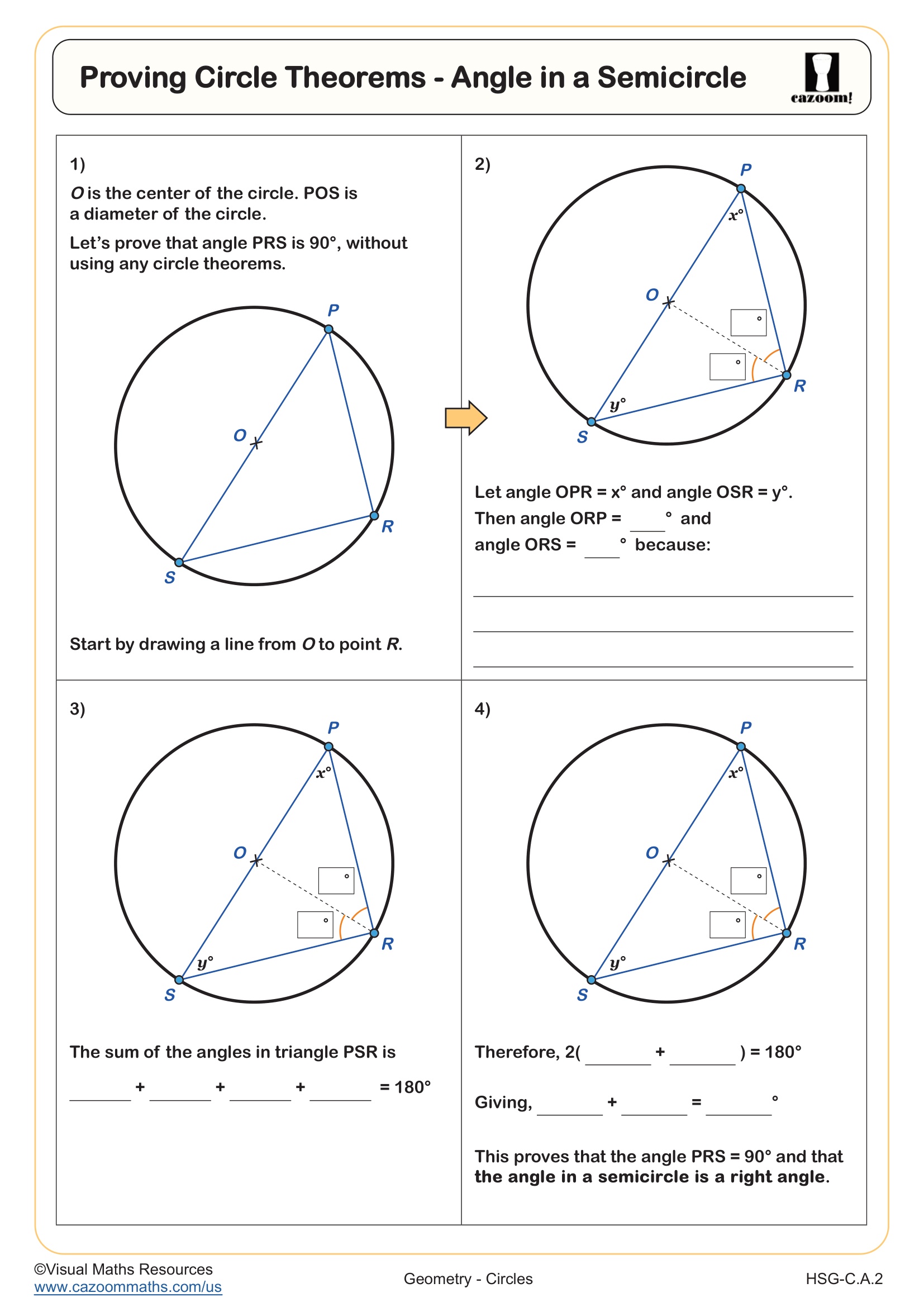
Proving Circle Theorems - Angles in the Same Segment
Grades: Geometry, IM 2
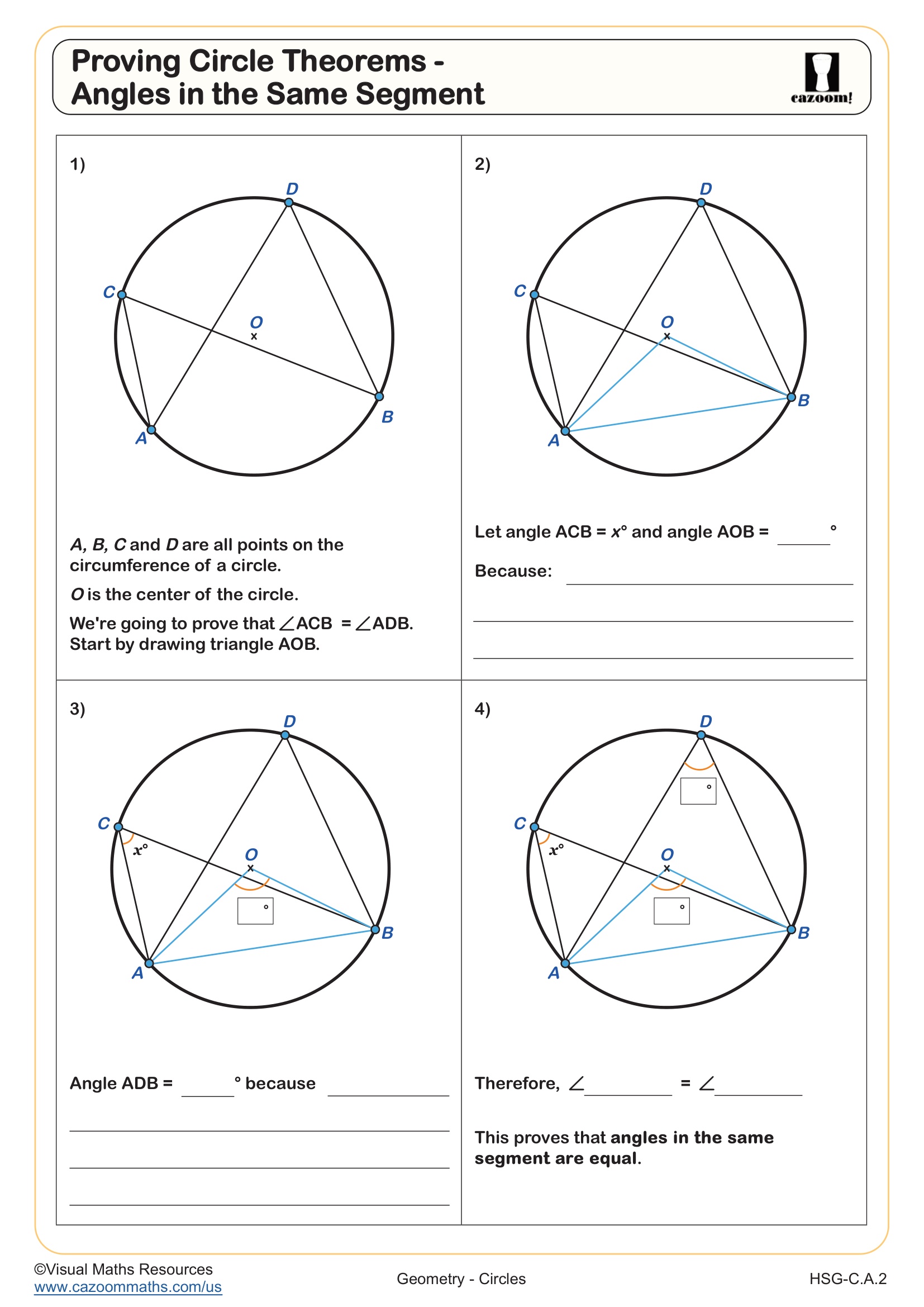
Proving Circle Theorems: Angle in the Center
Grades: Geometry, IM 1
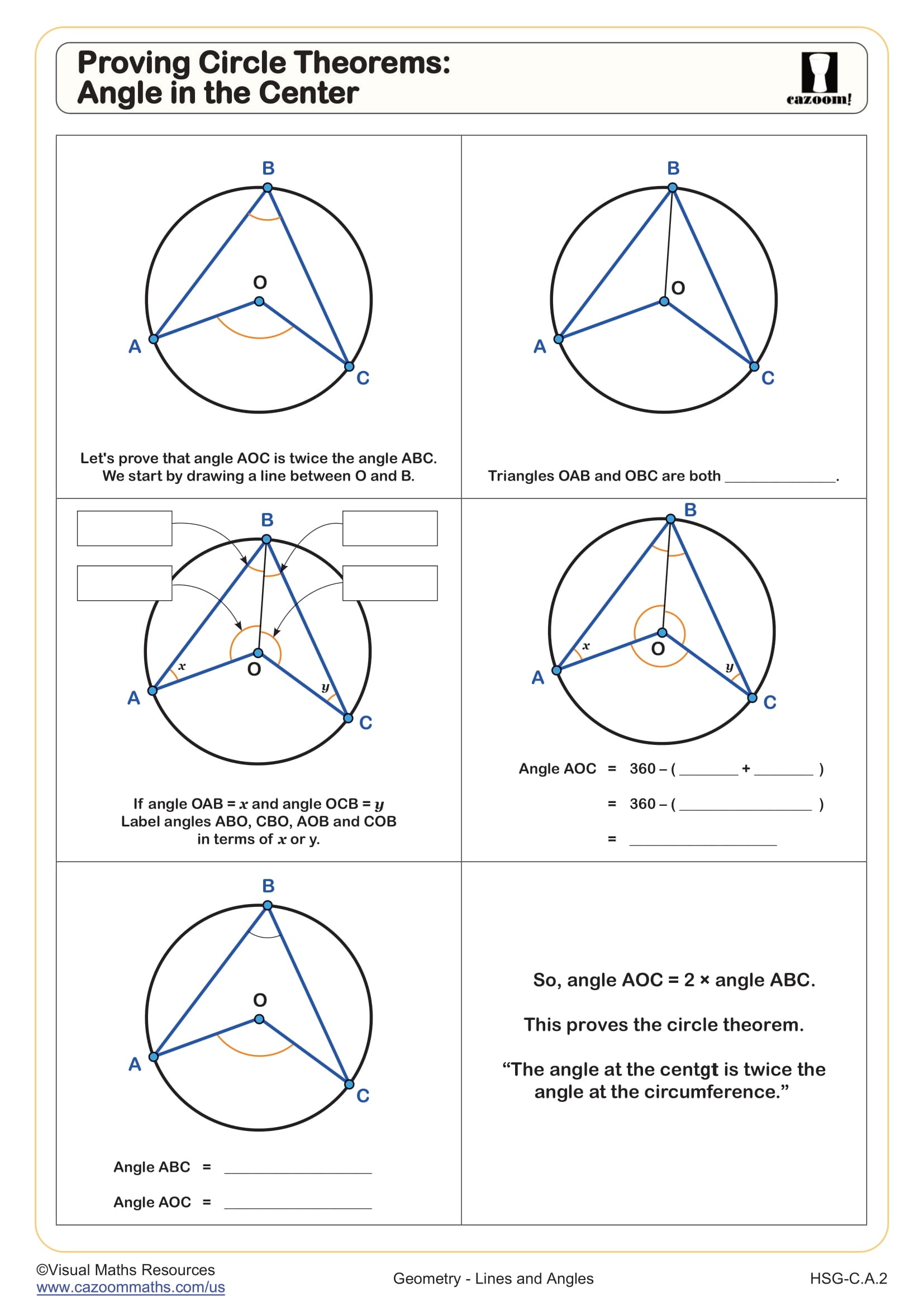
Proving Circle Theorems: Inscribed Quadrilaterals
Grades: Geometry, IM 1
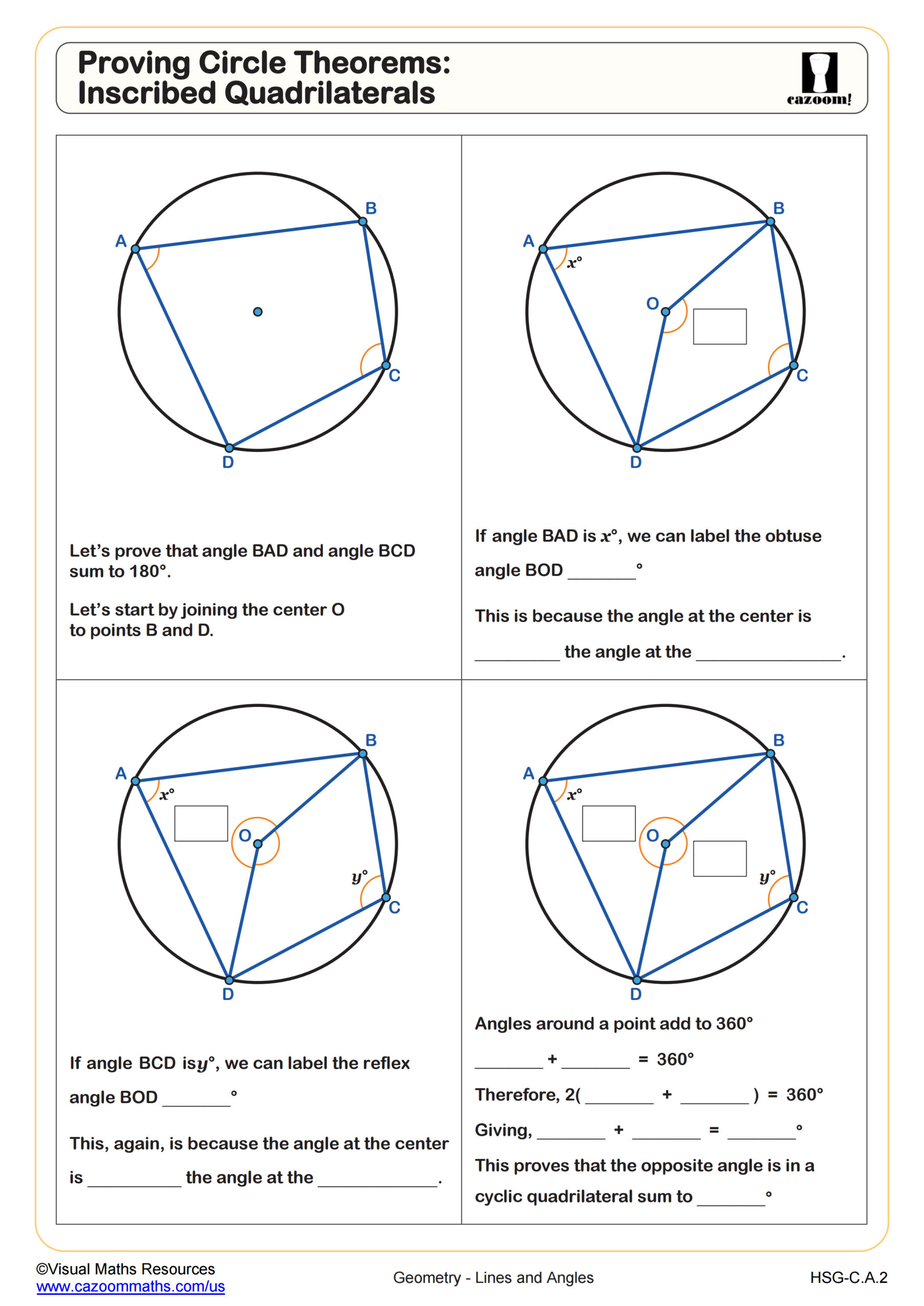
Volume With Pi (B)
Grades: Geometry, IM 2
Introducing Radians
Grades: Algebra II, IM 3

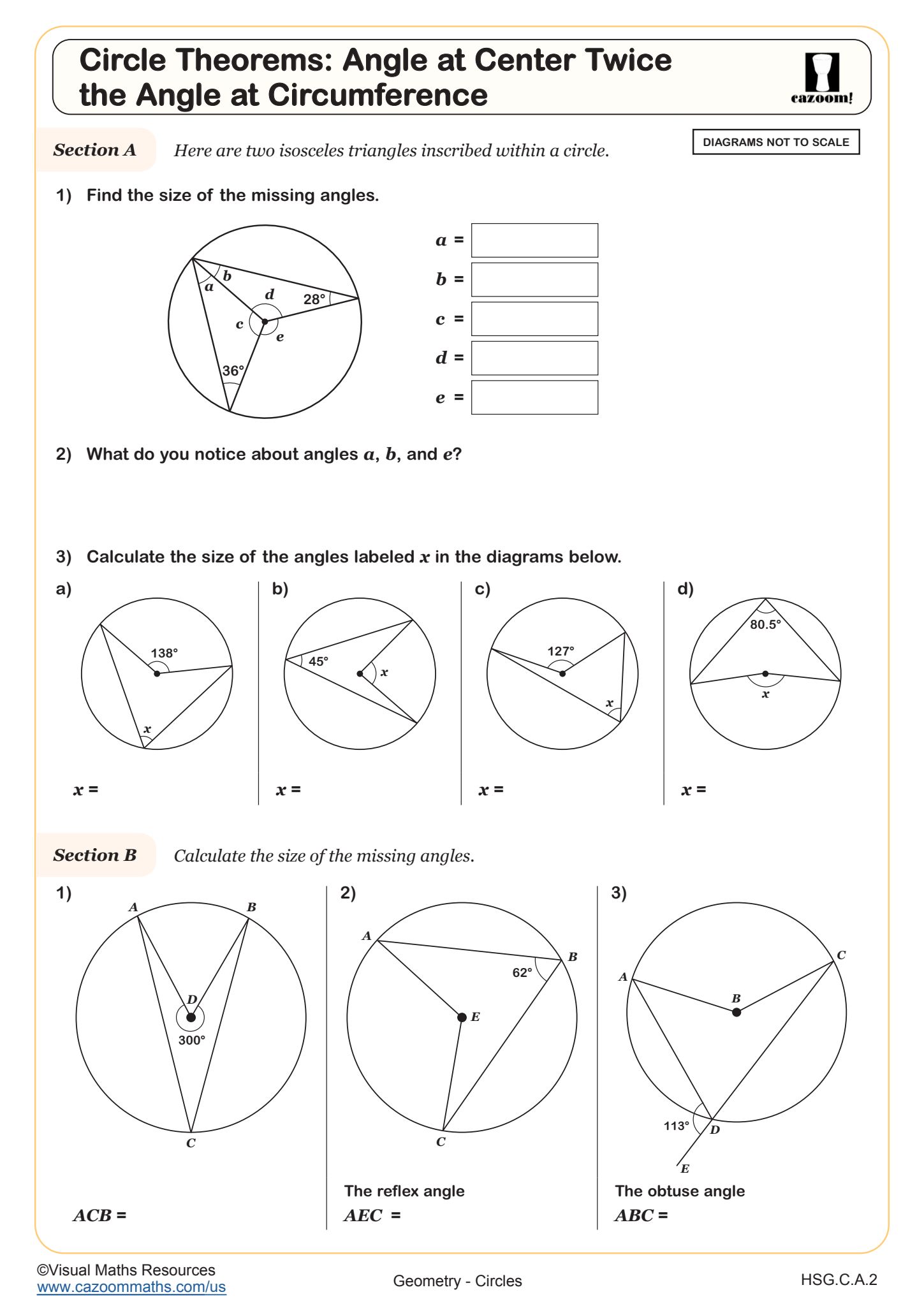
Circle Theorems: Angle at Center Twice the Angle at Circumference
Grades: IM 1
All worksheets are created by the team of experienced teachers at Cazoom Math.
Printable PDF Common Core Circles Worksheets with Answers
Learning the ins and outs of circles is an important part of math for your child or student. That is why Cazoom has supplied you with all the relevant circle worksheets and answers. Everything from area and circumference, radius, angles and tangents are provided for all abilities to whizz through.
HOW TO DETERMINE THE CIRCUMFERENCE AND AREA OF A CIRCLE?
Very often the circumference and the area of the circle are confused as the same thing, which is totally wrong. To determine the area and circumference of the circle first we need to explain these two terms.
WHAT IS THE CIRCUMFERENCE OF A CIRCLE?
The circumference of a circle is the distance around the outside of a circle. Basically, it is the perimeter like in any other geometric shape, like a square or a triangle. You can say that the circumference of a circle is the line that defines the shape. The main difference is that when a shape is made of straight edges it is called the perimeter, but when it comes to circles is called the circumference. Check out the image below.
Circumference
There are three defining aspects of every circle:
• The radius
• The diameter
• The circumference
The radius represents the distance from the center of the circle to any point of the circumference.
The diameter of a circle is the distance from one side of the circle to the widest point of the circumference. The diameter always passes through the center of the circle.
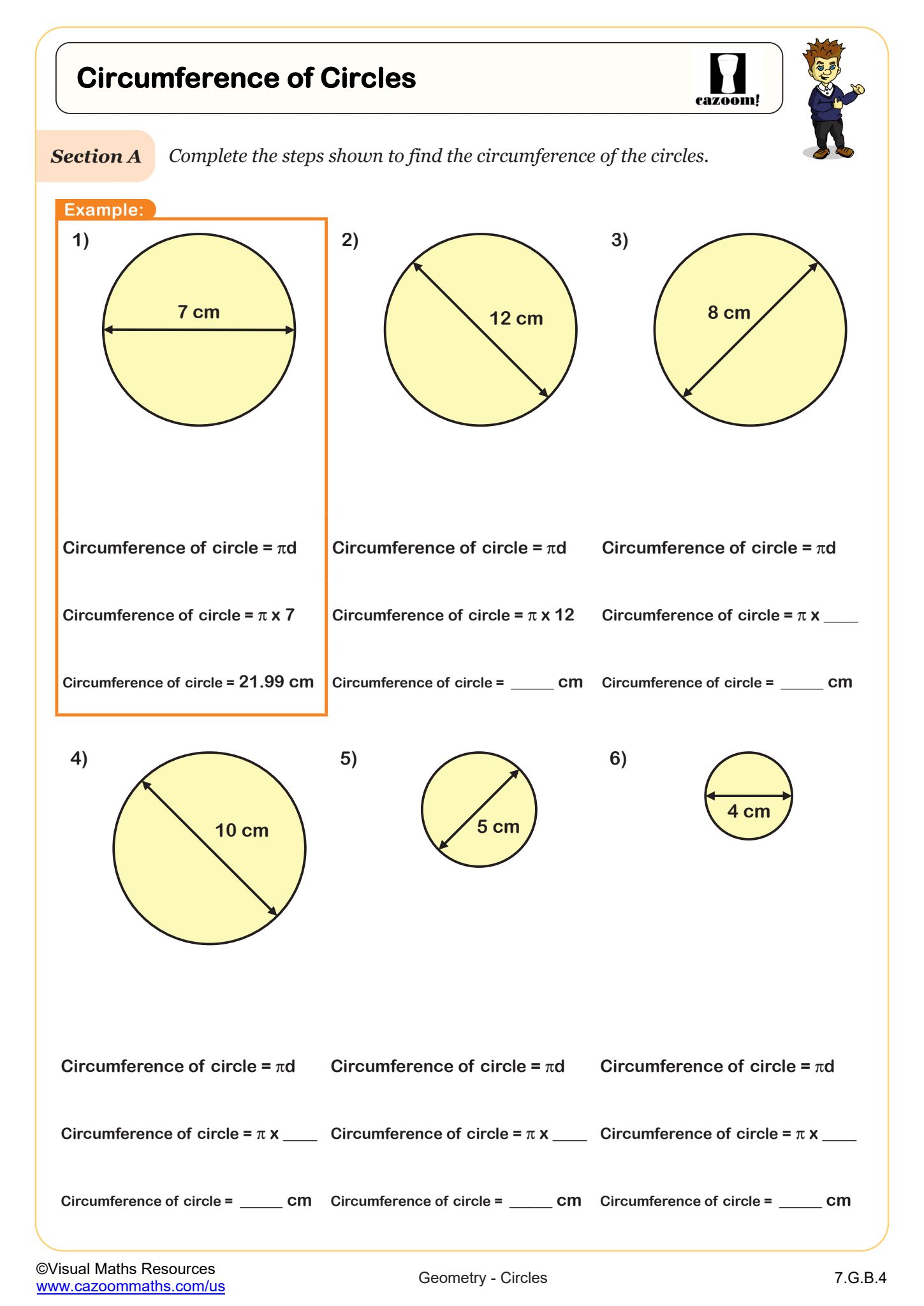
When we know the distance of the diameter of the circle it is really easy to calculate the circumference. We just need to multiply the diameter with pi (irrational number roughly equal to 3,14 written with the symbol π).
The circumference of a circle = π × diameter (C = πd)
Also, you can calculate the circumference if you know the radius of a circle. Always remember that the radius is half the length of the diameter. So, in this case C = 2πr.
EXAMPLE:
The diameter of a circle is 8 cm. Calculate the circumference.
C = 3,14 × 8
C = 25,12
Example 2:
The radius of a circle is 11 cm. Calculate the circumference.
C = 3,14 × 22
C = 69,08
Example:
The diameter of a circle is 8 cm. Calculate the circumference.
C = 3,14 x 8
C = 25,12
Example 2:
The radius of a circle is 11 cm. Calculate the circumference.
C = 3,14 x 22
C = 69,08
WHAT IS THE AREA OF A CIRCLE AND WHO TO CALCULATE IT?
The Area of a circle is the region occupied by the circle. To calculate the area of a circle we need to know the radius and diameter of the circle.
If we know the radius of the circle, we can use the following equation to calculate the area of the circle:
Area of the circle = π x r2
If we know the diameter of the circle, we can use the following equation to calculate the area of the circle:
Area of the circle = π x (r/2)2
Example:
The radius of a circle equals 3,4 cm. Calculate the area of the circle.
Area of the circle = 3,14 x 3,42
Area of the circle = 3,14 x 11,56
Area of the circle = 36,32 cm2
Example:
The diameter of a circle equals 8,2 cm. Calculate the area of the circle.
Area of the circle = 3,14 x (8,2/2)2
Area of the circle = 3,14 x 4,12
Area of the circle = 3,14 x 16,81
Area of the circle = 52,81 cm2