Geometry Circles Worksheets
Area of Arc Lengths & Sectors

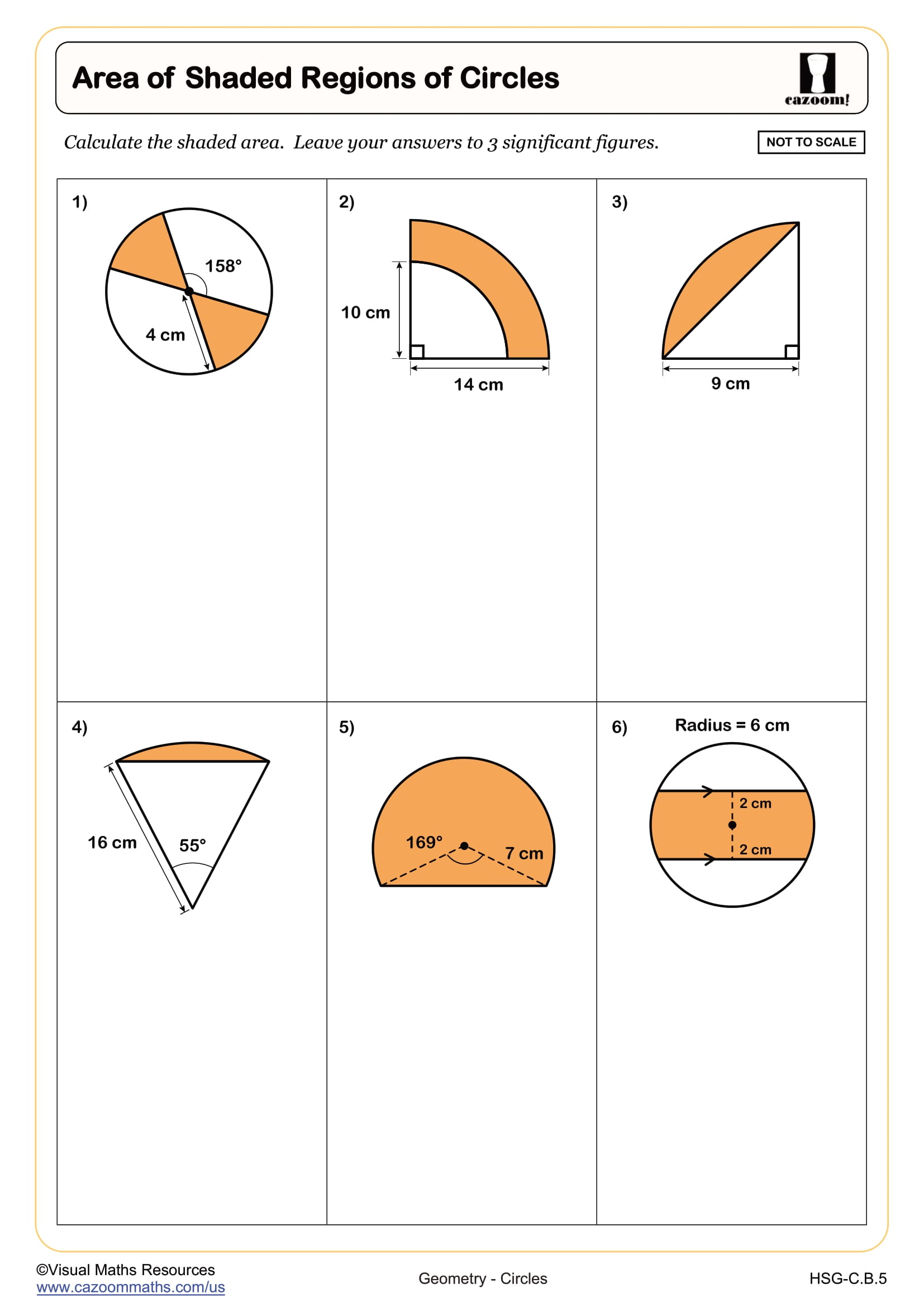
Area of Shaded Regions of Circles
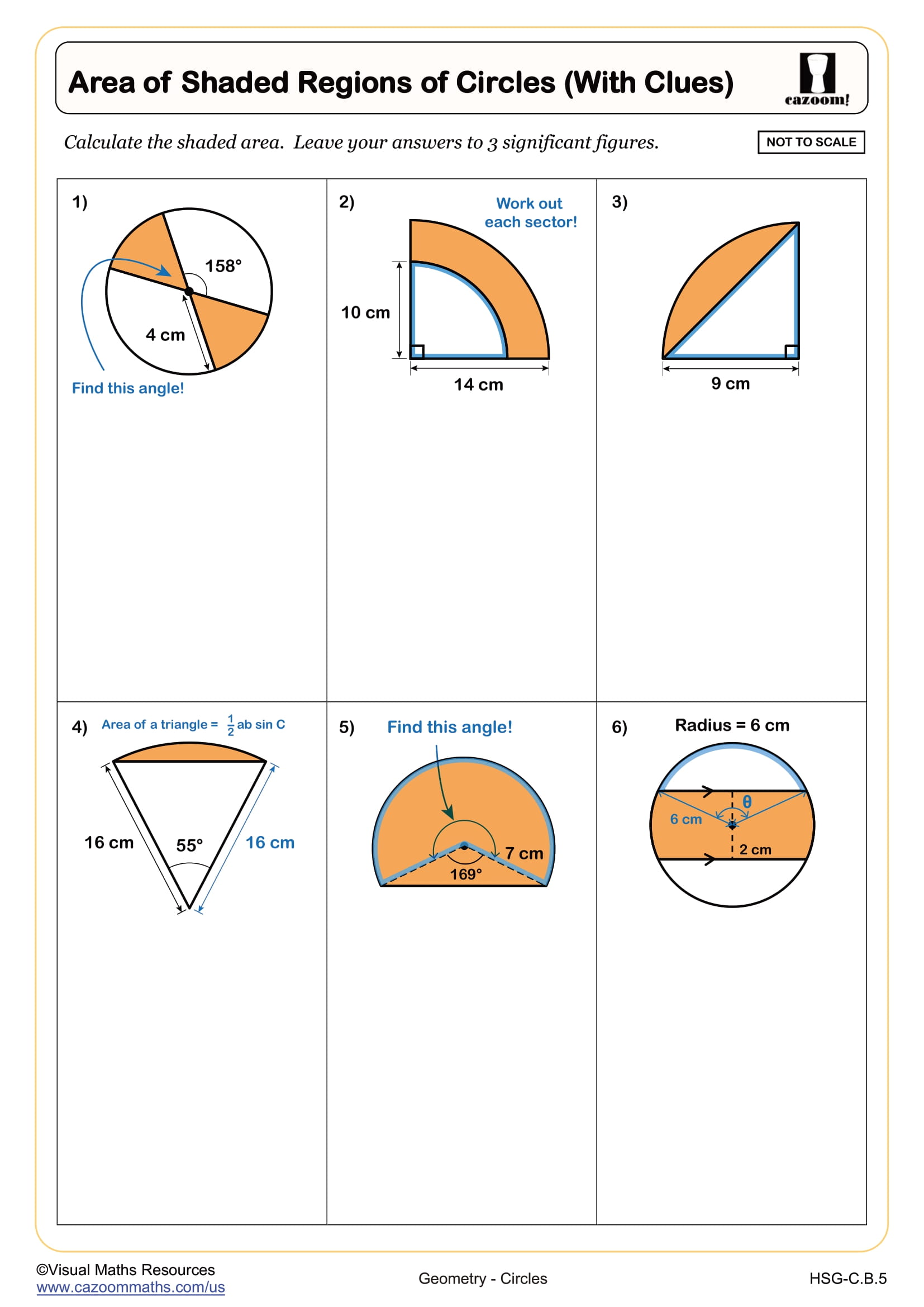
Area of Shaded Regions of Circles (with clues)
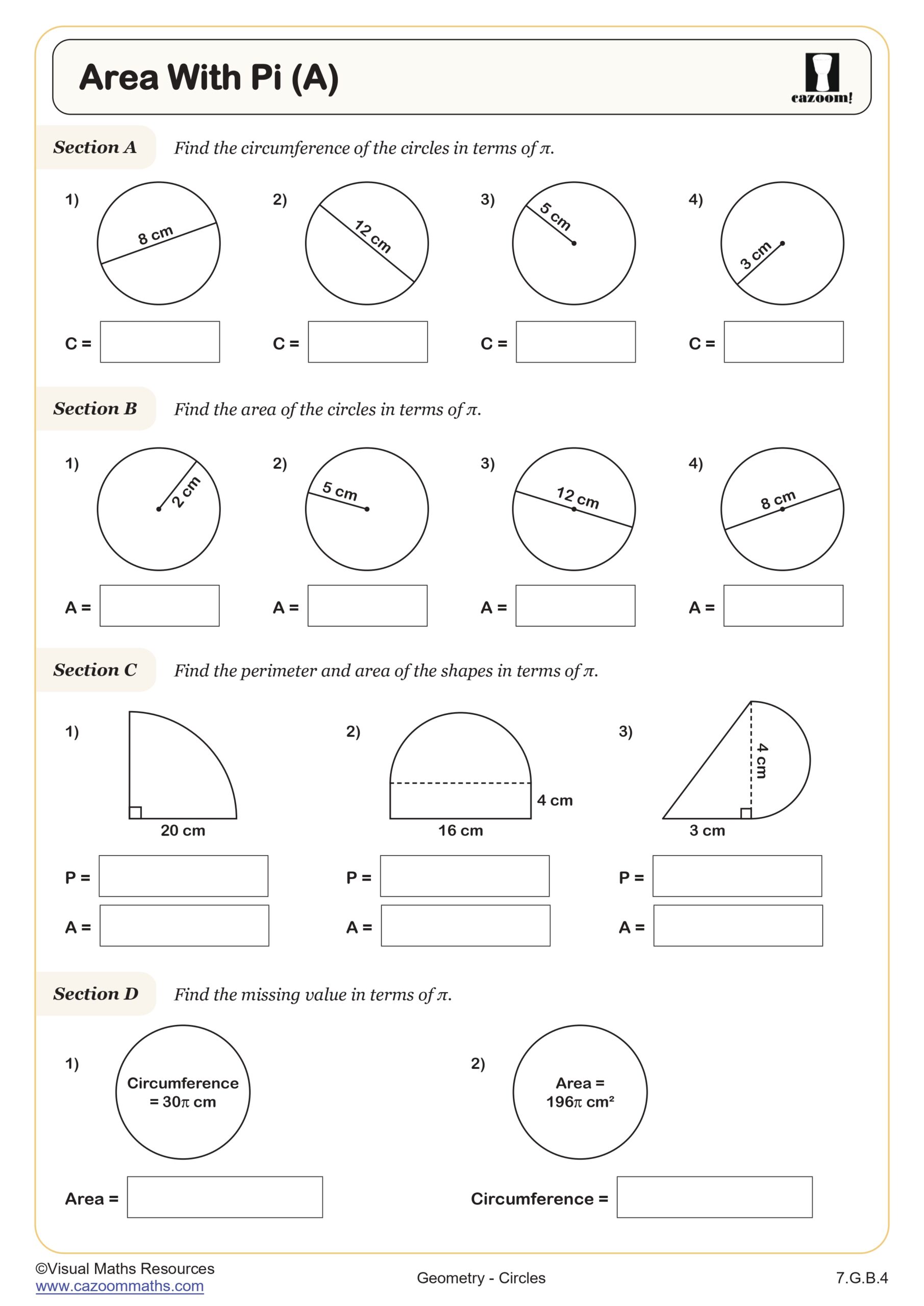
Area With Pi (A)
Circle Investigation - Discovering Pi

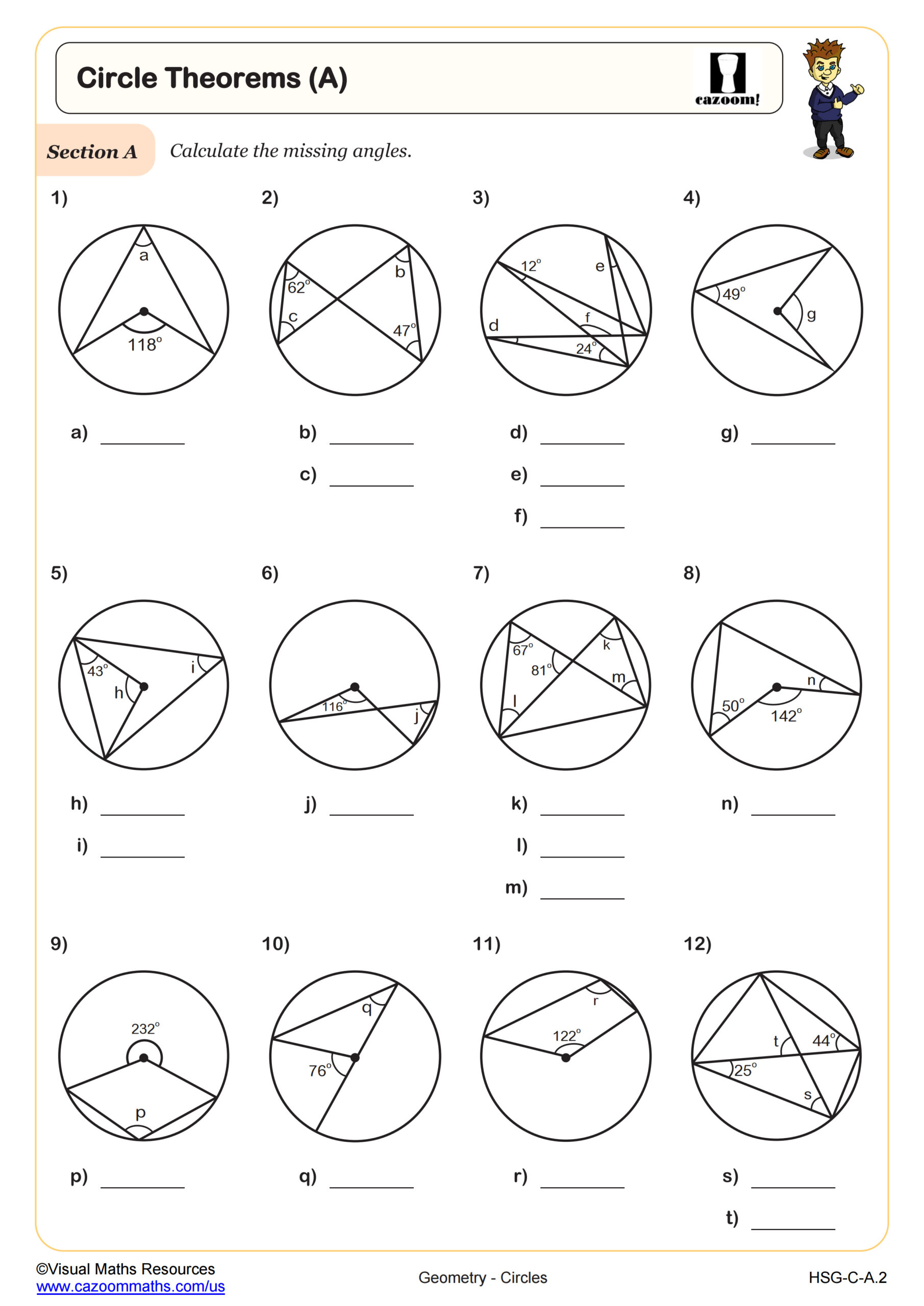
Circle Theorems (A)
Circle Theorems (B)
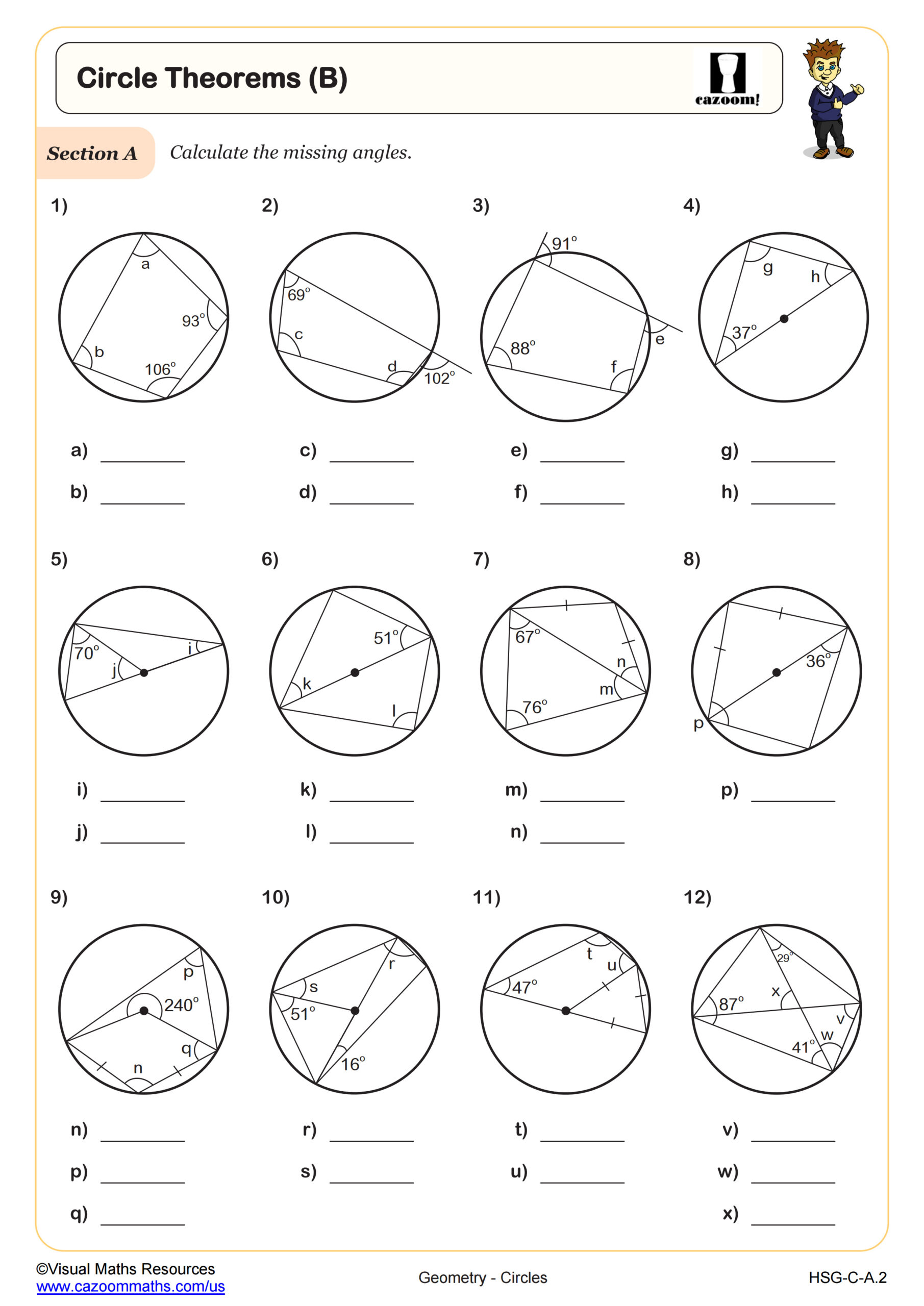
Circle Theorems (C)
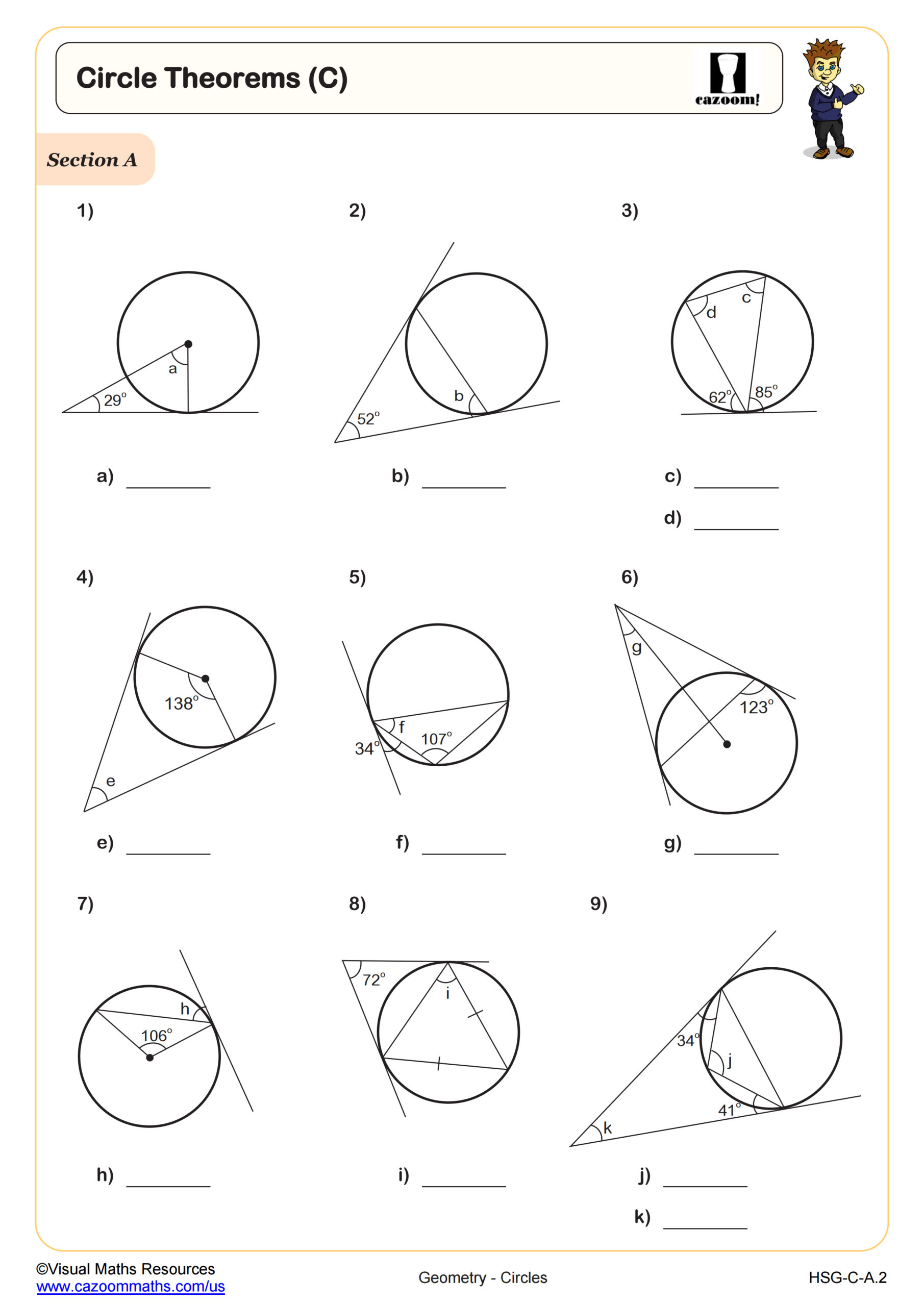
Circle Theorems: Angle Notation
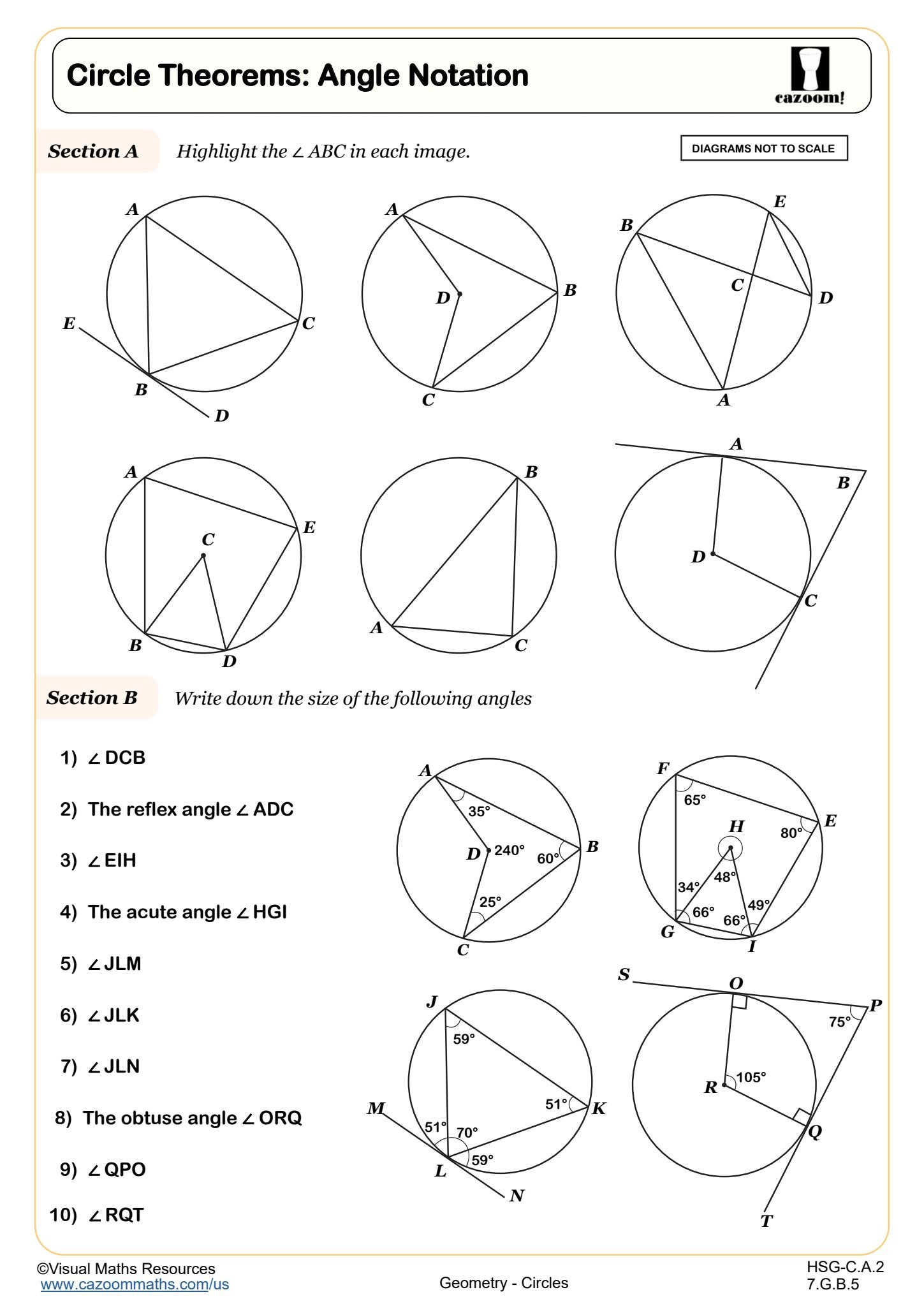
Circle Theorems: Cyclic Quadrilaterals
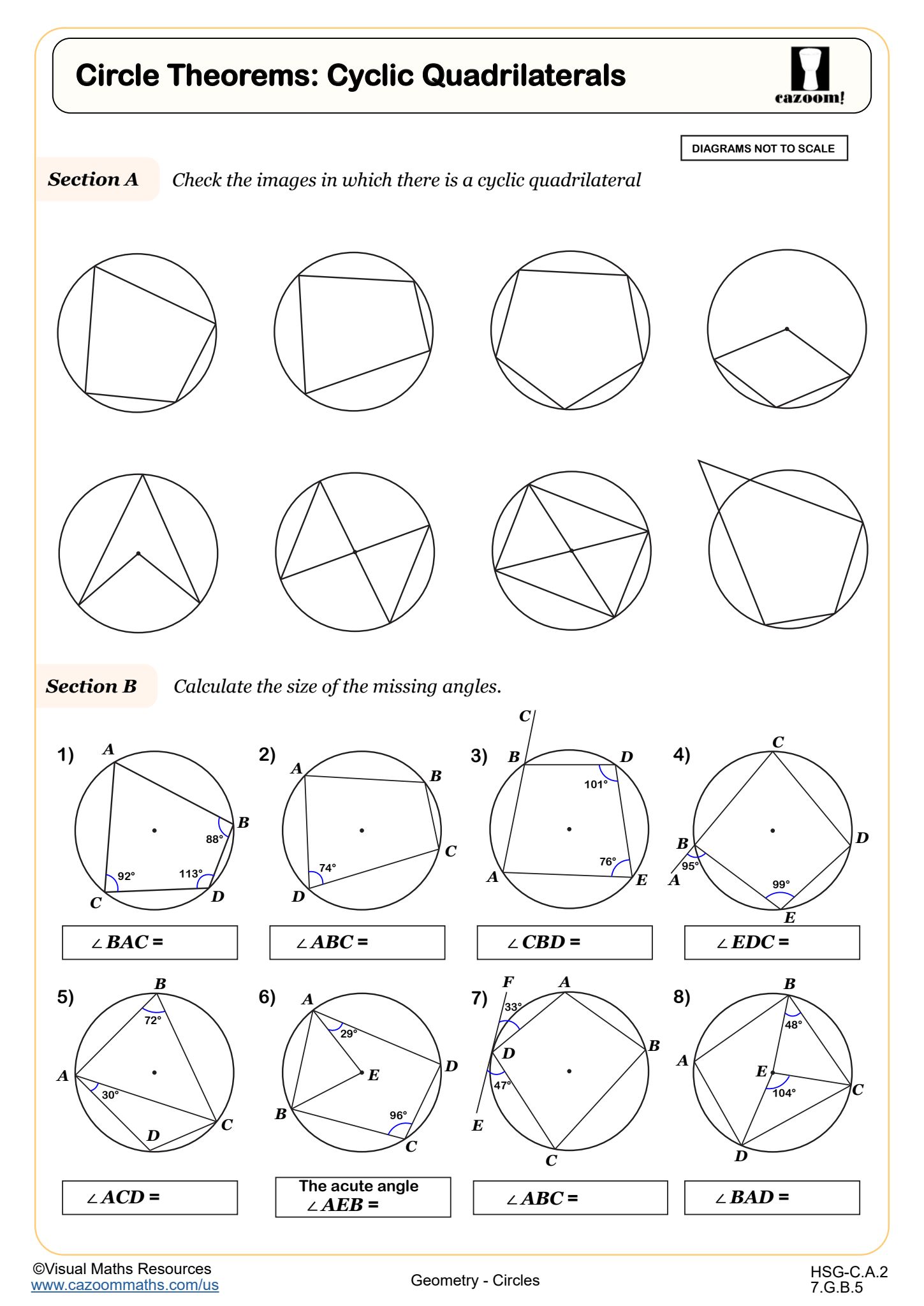
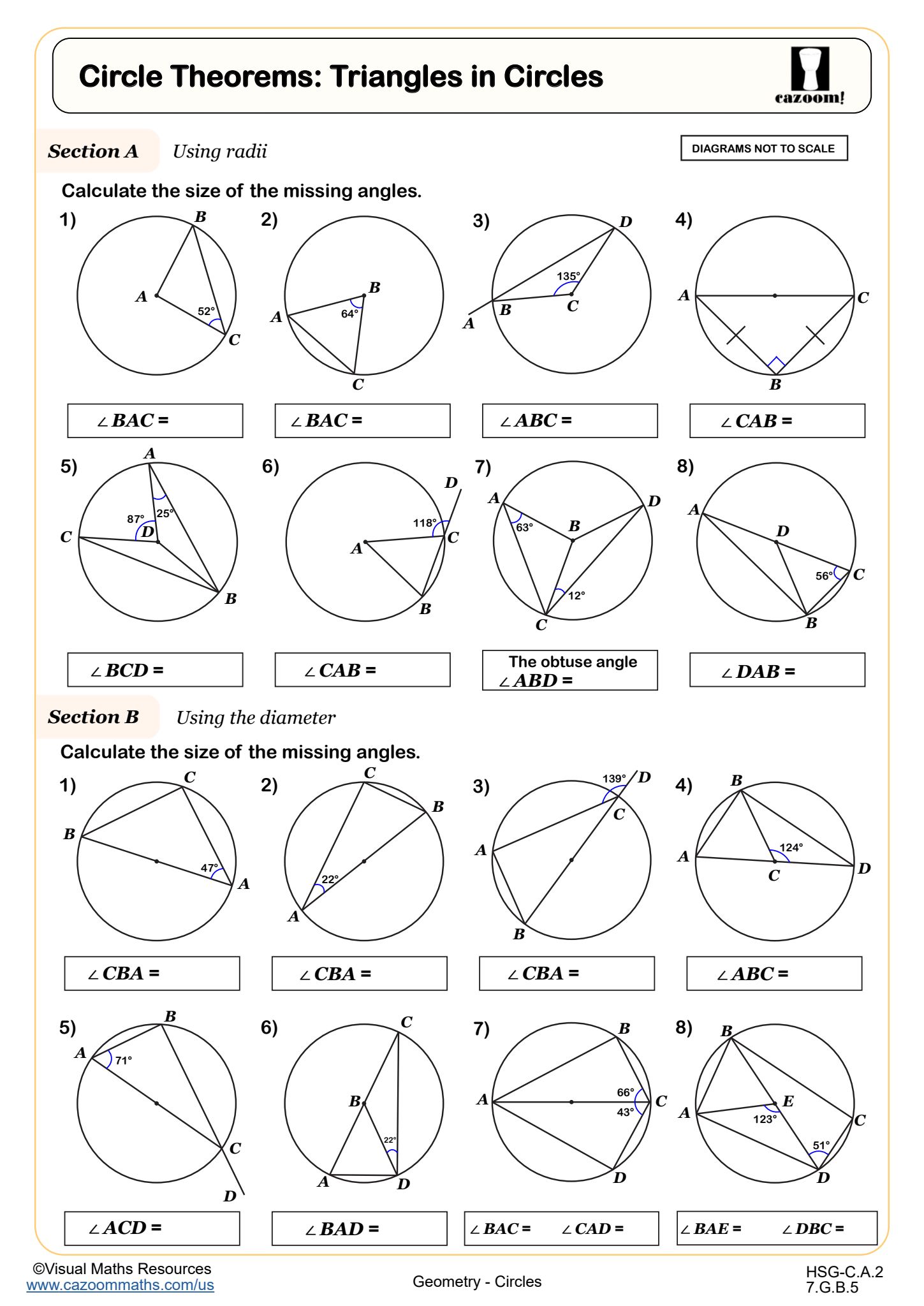
Circle Theorems: Triangles in Circles
Constructing an Easter Egg

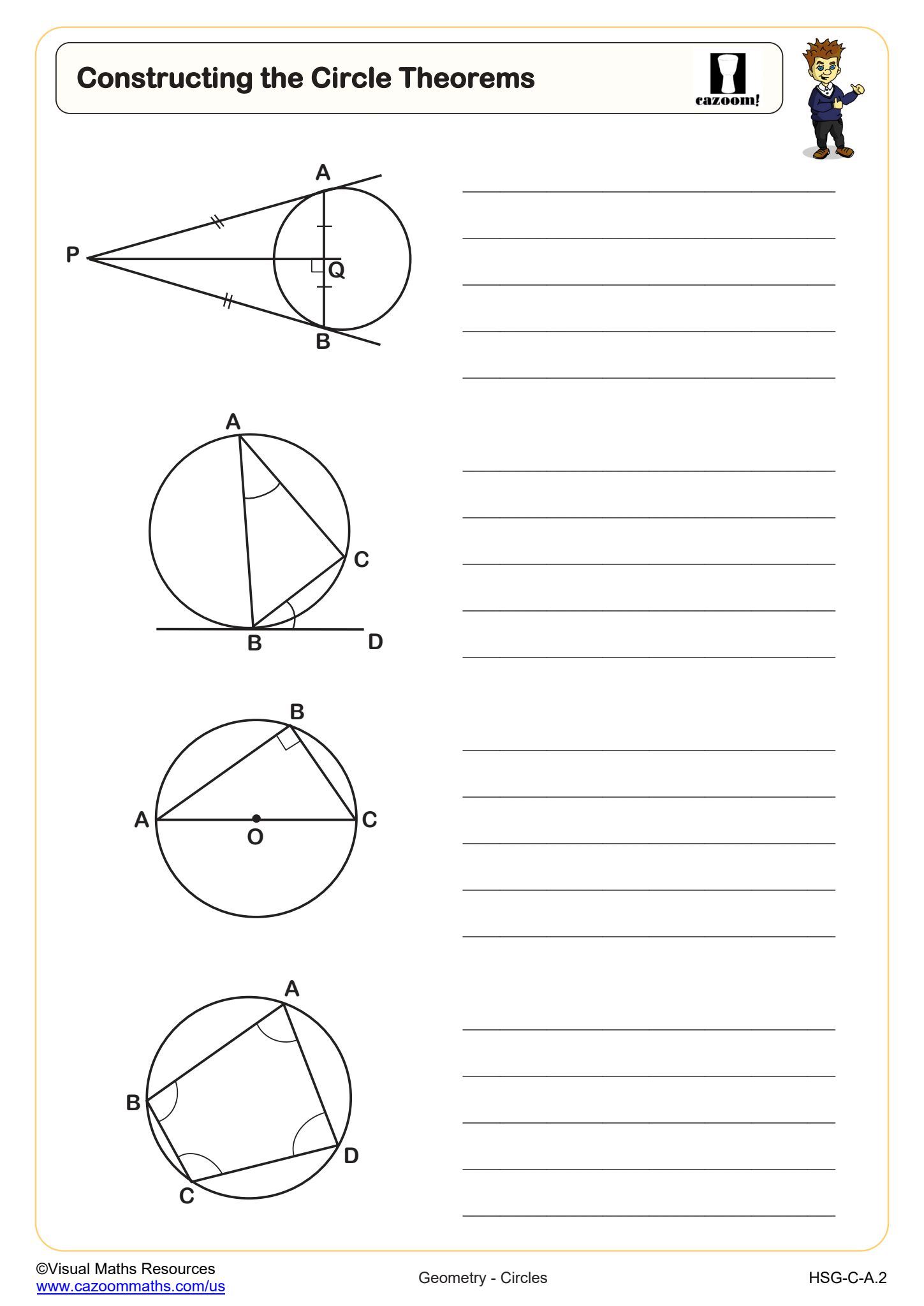
Constructing the Circle Theorems
Easter Egg Dimension

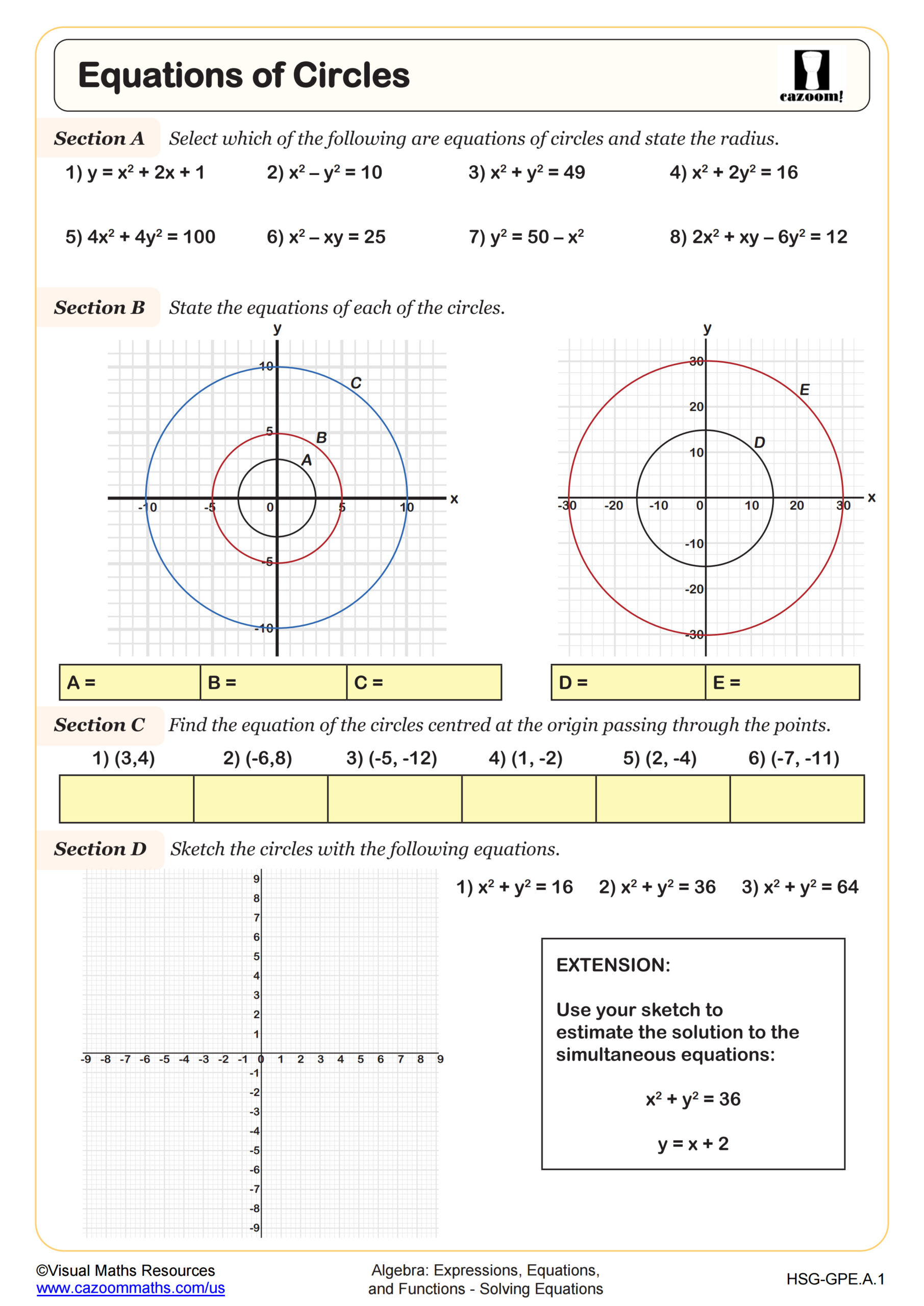
Equations of Circles
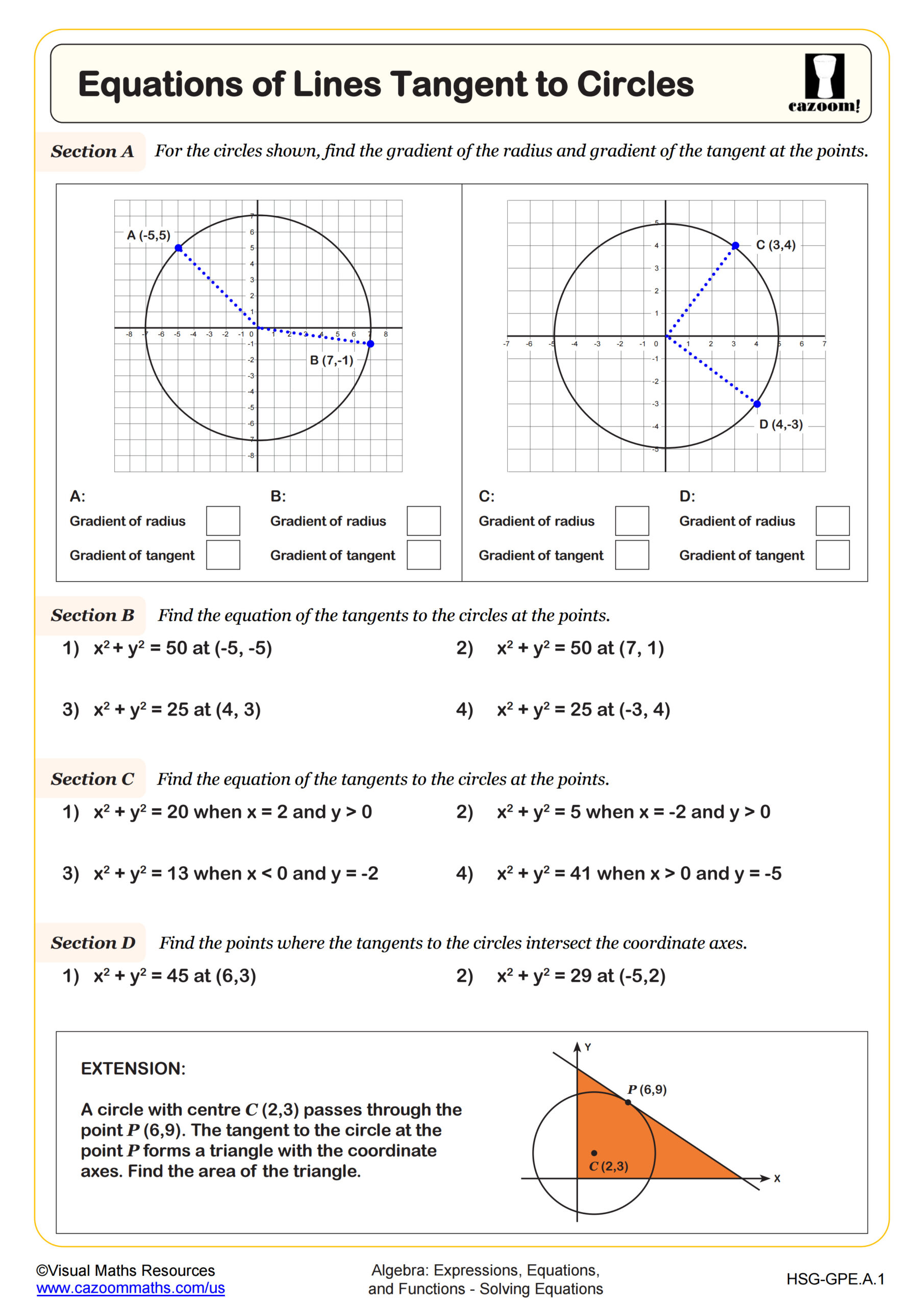
Equations of Lines Tangent to Circles
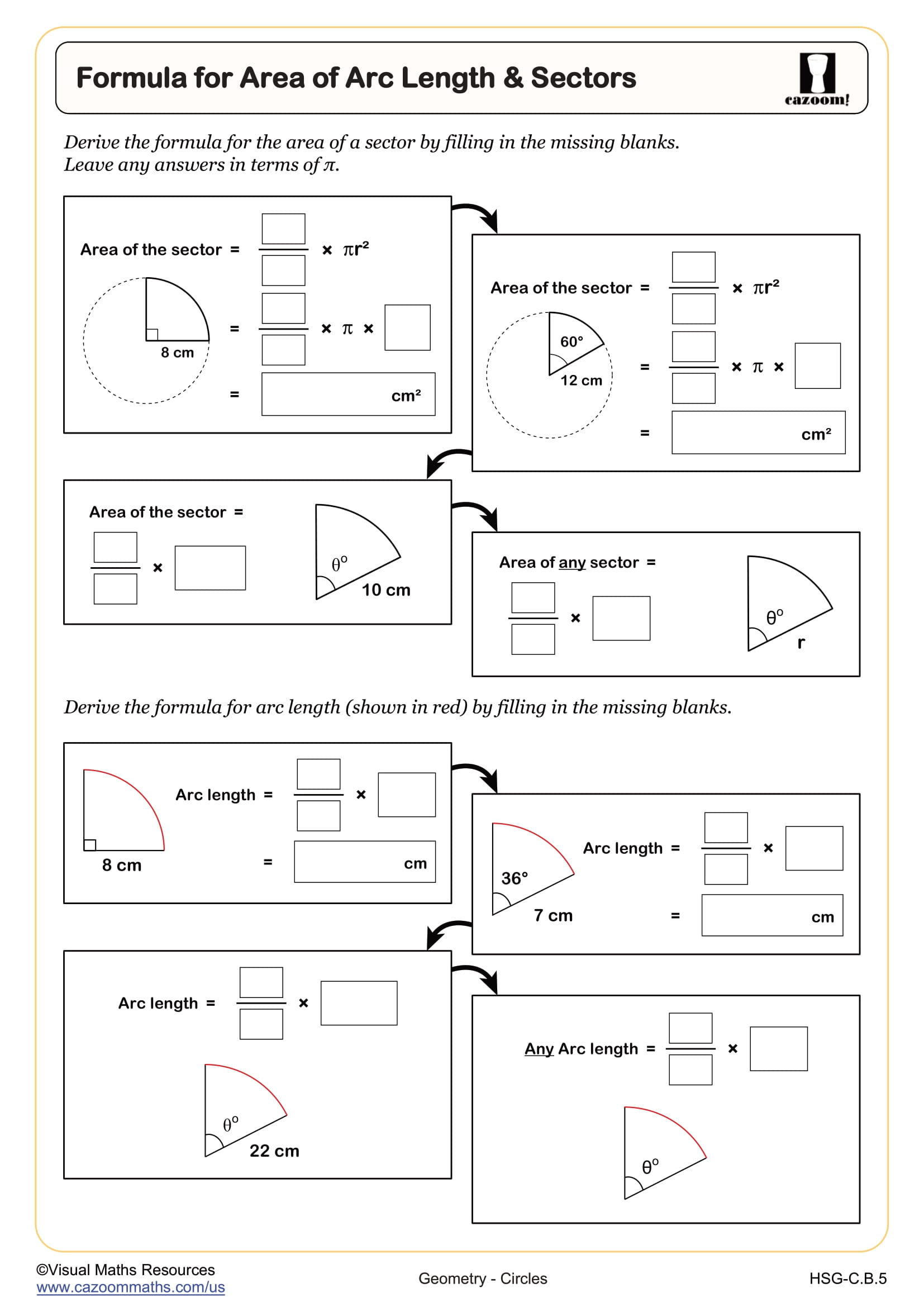
Formula for Area of Arc Length & Sectors
In Terms of Pi (B)

Pi (C)
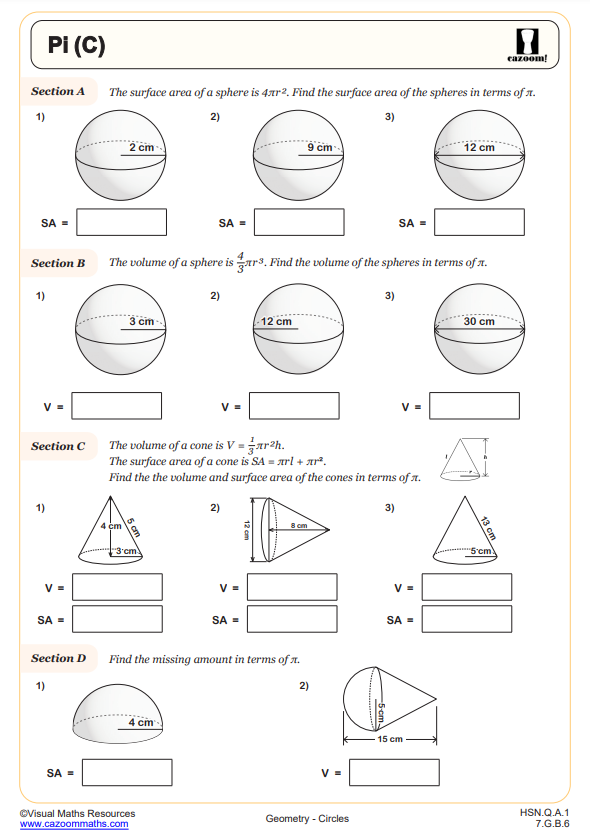
Proving Circle Theorems
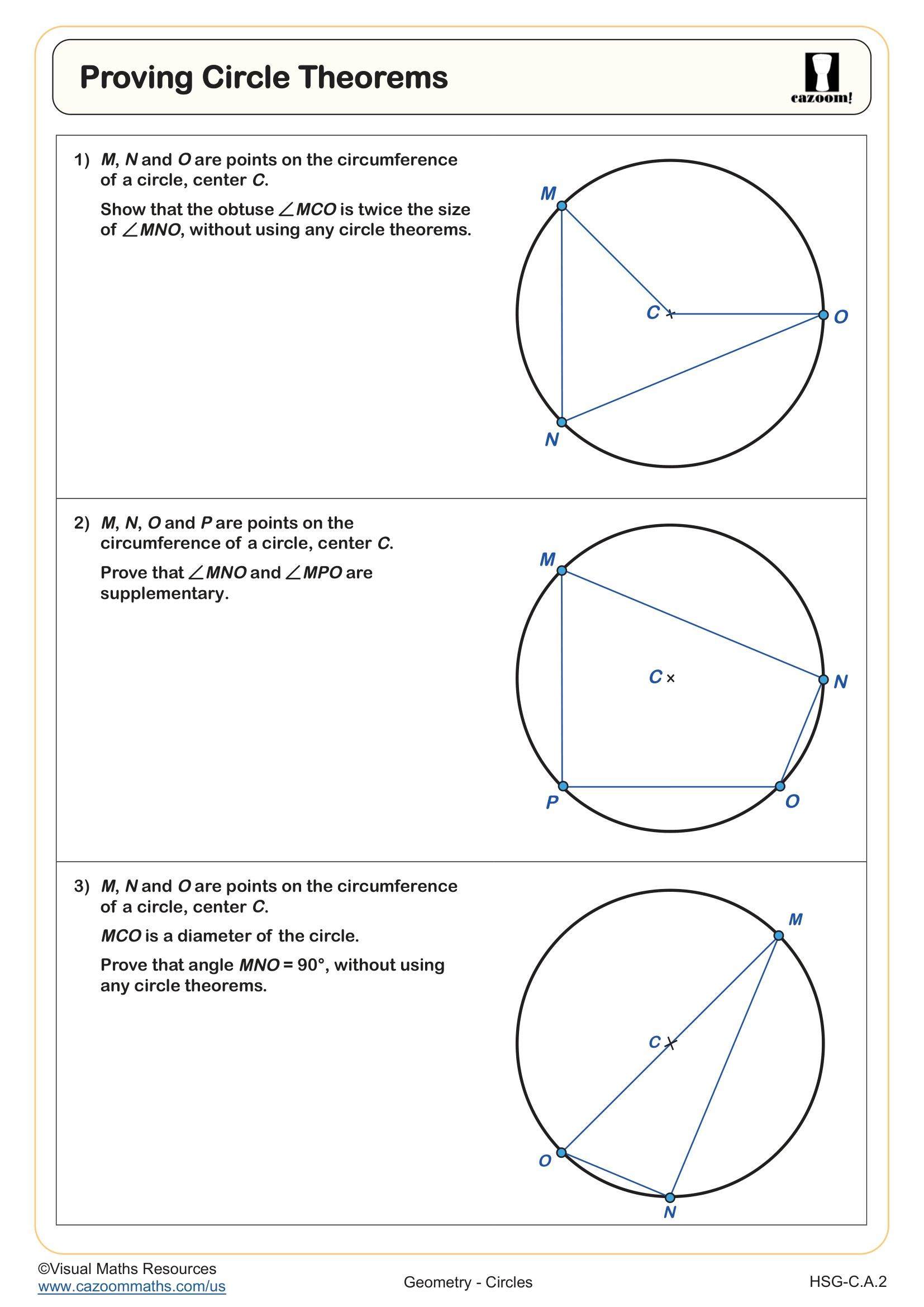
Proving Circle Theorems - Angle in a Semicircle
Proving Circle Theorems - Angles in the Same Segment
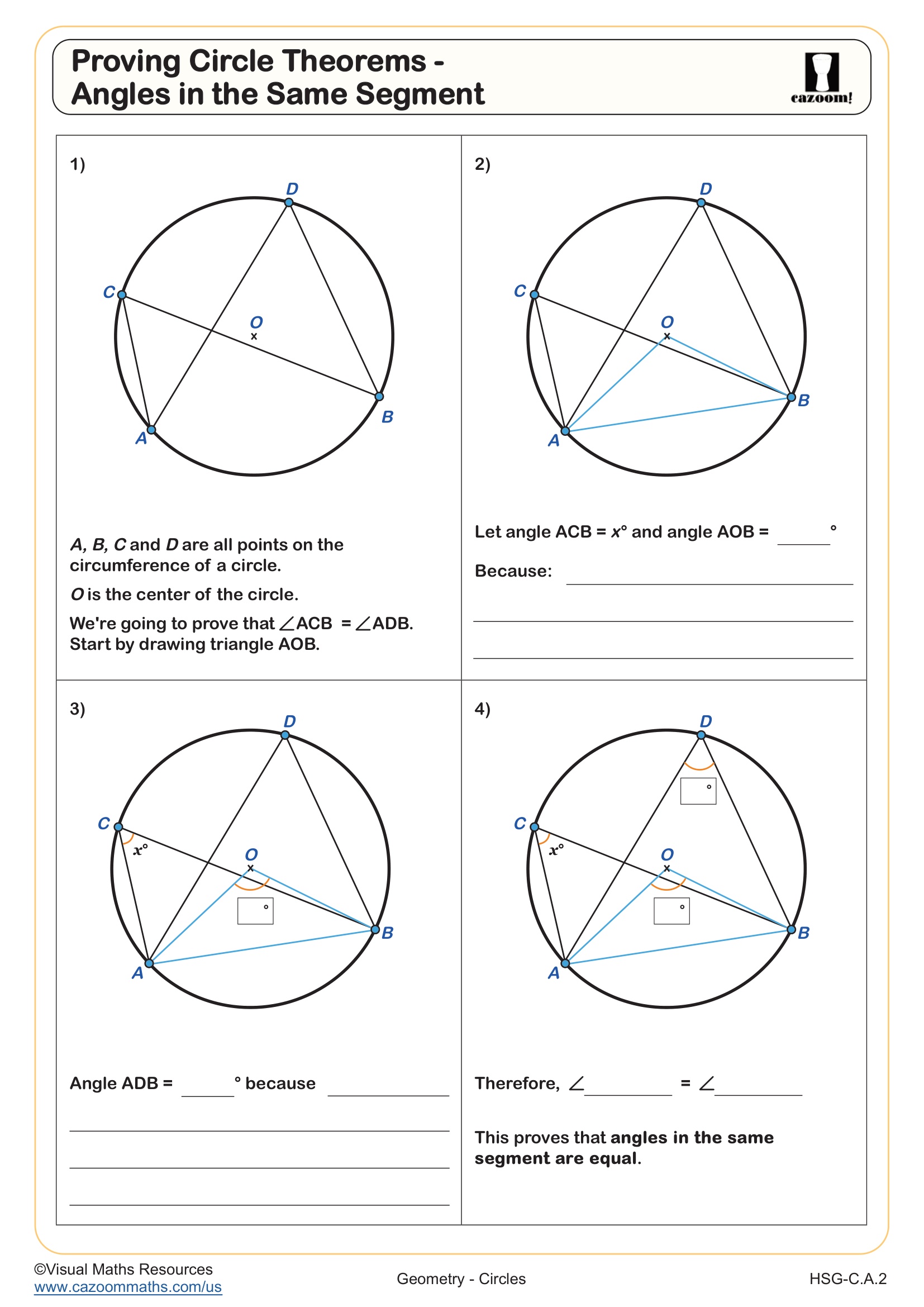
Proving Circle Theorems: Angle in the Center
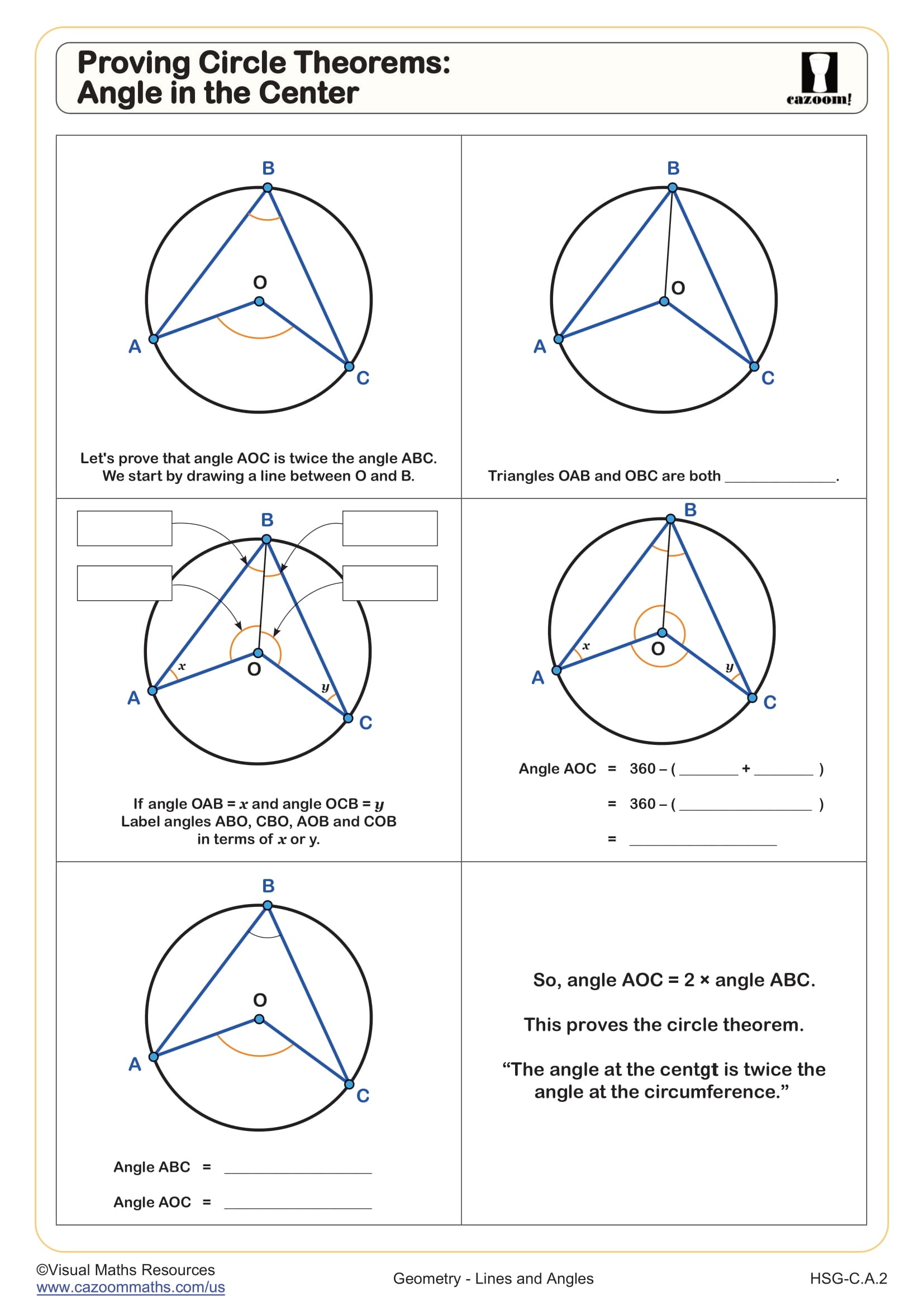
Proving Circle Theorems: Inscribed Quadrilaterals
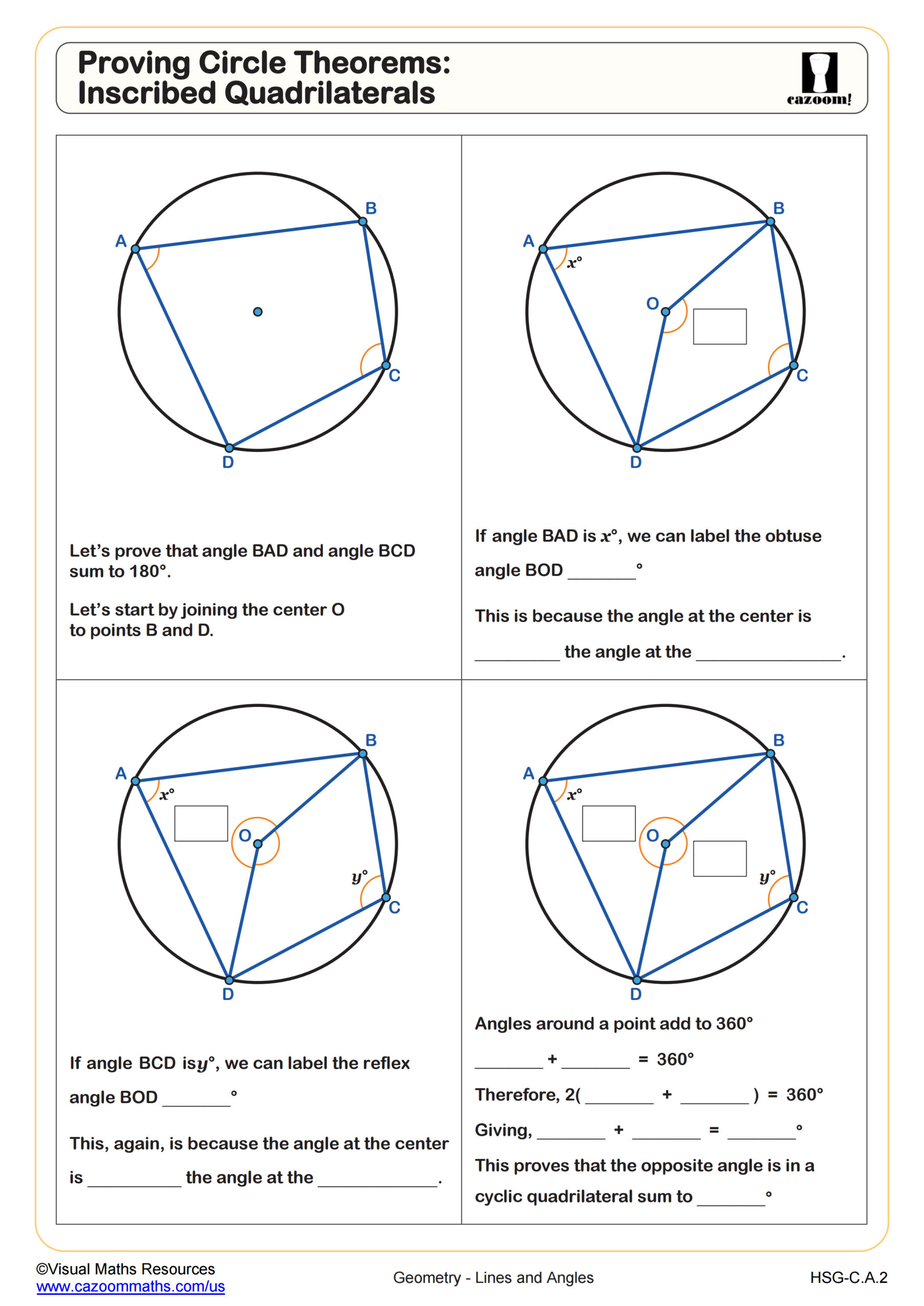
Volume With Pi (B)
What Circle Topics Do High School Geometry Students Study?
High school Geometry courses cover circles comprehensively, starting with fundamental properties like radius, diameter, and chord relationships, then progressing to circumference and area formulas involving π. Students learn to calculate arc length and sector area, work with central and inscribed angles, and apply the inscribed angle theorem. More advanced topics include tangent-radius relationships, angles formed by chords and secants, and segment length relationships when chords intersect. The curriculum culminates in formal proofs of classic circle theorems that appear throughout standardized assessments.
Many students initially confuse inscribed angles with central angles, forgetting that inscribed angles measure half the intercepted arc. Teachers frequently observe students attempting to apply the inscribed angle theorem to angles formed by tangents or secants, which requires different reasoning. The breakthrough typically happens when students sketch multiple examples and physically measure angles to verify the 2:1 relationship between central and inscribed angles subtending the same arc.
How Are Circles Tested on the SAT and State Geometry Assessments?
Standardized tests like the SAT and ACT assess circle concepts through multi-step problems that combine coordinate geometry with circle properties, area and circumference calculations in applied contexts, and angle relationships within circles. Students must interpret diagrams showing tangent lines, inscribed polygons, or intersecting chords, then apply appropriate theorems to find missing measures. The SAT particularly favors problems involving circles in the coordinate plane, requiring students to write equations or identify center and radius from standard form.
Students lose points when they misapply formulas, confusing area (πr²) with circumference (2πr) under time pressure, or when they fail to recognize that tangent lines form right angles with radii at the point of tangency. Another common assessment error occurs when students see a quadrilateral inscribed in a circle but forget that opposite angles must be supplementary. Teachers notice that students who practice identifying which theorem applies in various configurations perform significantly better than those who only memorize isolated formulas.
What Are Circle Theorems and Why Do Students Prove Them?
Circle theorems are geometric relationships that consistently hold true for all circles, including the inscribed angle theorem, the angle in a semicircle theorem (which states that any angle inscribed in a semicircle measures 90°), and theorems about inscribed quadrilaterals. Proving these theorems develops deductive reasoning skills and reinforces why these relationships work, not just that they work. Students construct logical arguments using previously established postulates, definitions, and theorems, building mathematical maturity that transfers to trigonometry, calculus, and college-level mathematics courses.
Circle theorems appear extensively in engineering and architecture, particularly in structural design where arches and circular supports distribute weight efficiently. Satellite dish design relies on parabolic reflectors, but the underlying mathematics builds directly on circle geometry principles. Urban planners use circle theorems when designing traffic roundabouts and determining optimal positioning for streetlights to achieve uniform coverage. Students pursuing STEM fields encounter these concepts again in physics when studying orbital mechanics and wave propagation.
How Can Teachers Use These Circle Worksheets in Geometry Classes?
These worksheets scaffold circle concepts from basic properties through complex proofs, allowing teachers to differentiate instruction based on student readiness. Worksheets covering π and basic formulas establish foundational skills, while theorem proof worksheets challenge advanced students to construct formal arguments. The included answer keys enable students to check their work independently during practice sessions, promoting metacognition as they identify which types of problems require additional attention. Teachers can assign specific worksheets targeting concepts that appeared on recent quizzes or formative assessments.
Many teachers use these materials for targeted test preparation, assigning mixed review worksheets before unit exams or state assessments. Circle theorem worksheets work well for paired activities where students collaborate on proofs, verbalizing their reasoning to identify logical gaps. Teachers also find these resources valuable for intervention sessions with students who struggled on initial assessments, providing fresh practice problems without simply repeating the same textbook exercises. The variety of problem types across the collection supports spaced practice throughout the semester, helping students retain circle concepts long-term rather than forgetting them immediately after the unit test.