Geometry Constructions Worksheets
What Do Geometry Constructions Worksheets Cover?
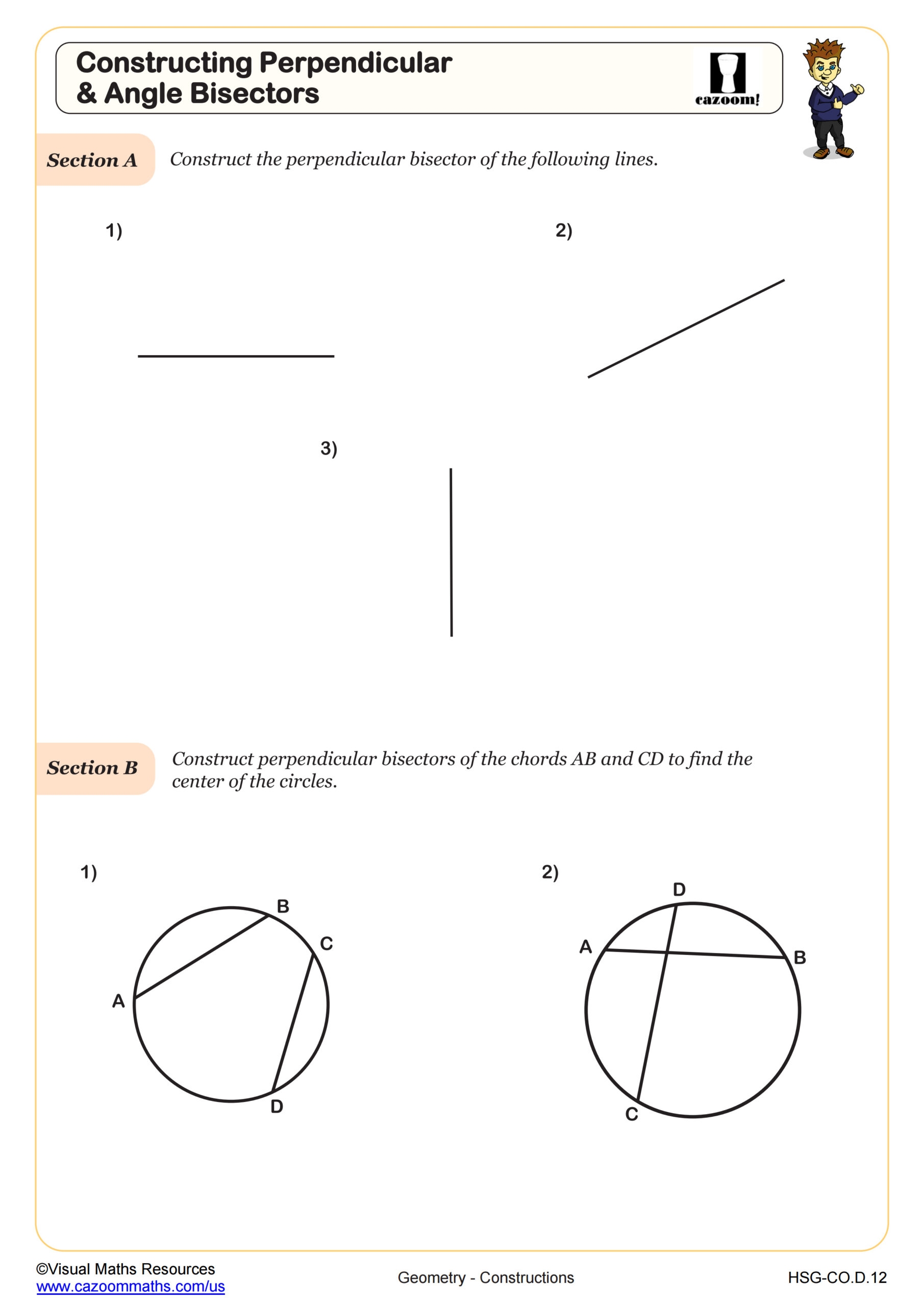
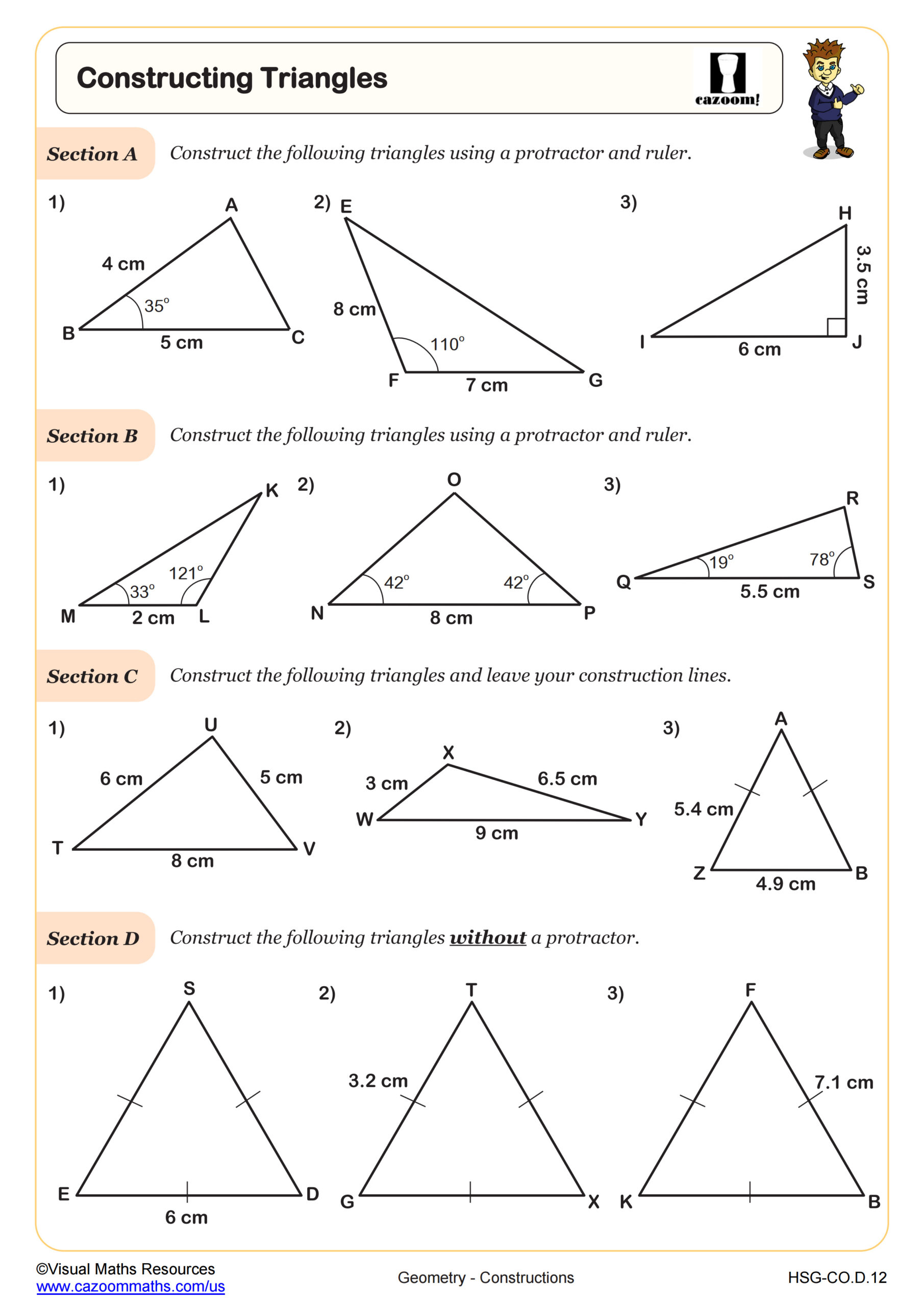
Geometry construction worksheets focus on classical compass and straightedge techniques aligned with Common Core Standard G-CO.D.12 and G-CO.D.13. Students practice constructing perpendicular bisectors, angle bisectors, equilateral triangles, and inscribed or circumscribed circles. These worksheets emphasize the step-by-step process of creating accurate geometric figures without measuring tools, relying instead on the properties of circles and line segments.
A common error students make is confusing perpendicular bisectors with angle bisectors, particularly when working with triangles where both constructions appear similar. Teachers often use color coding during instruction to help students distinguish between these two fundamental constructions, noting that perpendicular bisectors create right angles with sides while angle bisectors divide vertex angles into equal parts. This distinction becomes critical when students tackle more complex problems involving triangle centers.
How Do Constructions Appear on Standardized Tests?
While the SAT and ACT rarely require students to perform actual compass-and-straightedge constructions, state assessments and classroom tests frequently include questions about construction properties and sequences. Students need to recognize the characteristics of properly constructed bisectors, identify which construction technique produces specific results, and understand the mathematical reasoning behind why constructions work. Questions often ask students to determine which diagram shows a correct construction or to explain why a particular sequence of steps creates the desired figure.
Students lose points when they cannot justify why construction steps work or when they confuse the order of operations in multi-step constructions. For example, when constructing an inscribed circle in a triangle, students must first create angle bisectors to locate the incenter, then construct a perpendicular from that point to any side. Mixing up this sequence or failing to explain the logic results in lost credit even when the final diagram looks approximately correct.
What Are Perpendicular and Angle Bisectors Used For?
Perpendicular bisectors divide line segments into two equal parts at right angles, while angle bisectors split angles into two congruent angles. Both constructions serve as foundation skills for locating triangle centers: perpendicular bisectors intersect at the circumcenter, and angle bisectors meet at the incenter. Students learn that any point on a perpendicular bisector is equidistant from the segment's endpoints, while any point on an angle bisector is equidistant from the angle's sides.
These bisector properties appear in civil engineering and architecture when determining optimal locations for structures. Urban planners use perpendicular bisector principles to find equidistant points when placing fire stations or cell towers to serve multiple communities efficiently. Surveyors rely on angle bisector concepts when dividing land parcels or establishing property boundaries that must maintain equal distances from existing reference lines.
How Can Teachers Use Construction Worksheets Effectively?
Construction worksheets work best when students have access to quality geometry tools and understand that precision matters more than speed. The worksheets progress from single-step constructions like perpendicular bisectors to complex multi-step problems like inscribed circles, allowing teachers to differentiate instruction based on student readiness. Answer keys showing proper arc marks and construction lines help students develop self-assessment skills, comparing their work step-by-step rather than just checking final answers.
Many teachers use these worksheets during geometry units on triangle congruence and similarity, since construction skills reinforce why SSS, SAS, and ASA conditions guarantee congruence. The mixed practice sheets serve as effective spiral review before chapter tests or as targeted intervention for students who need additional construction exposure. Partner activities work particularly well, with one student performing constructions while another verifies each step using the answer key, then switching roles for the next problem.