Geometry Properties of Shapes Worksheets
What Shape Properties Do High School Geometry Students Study?
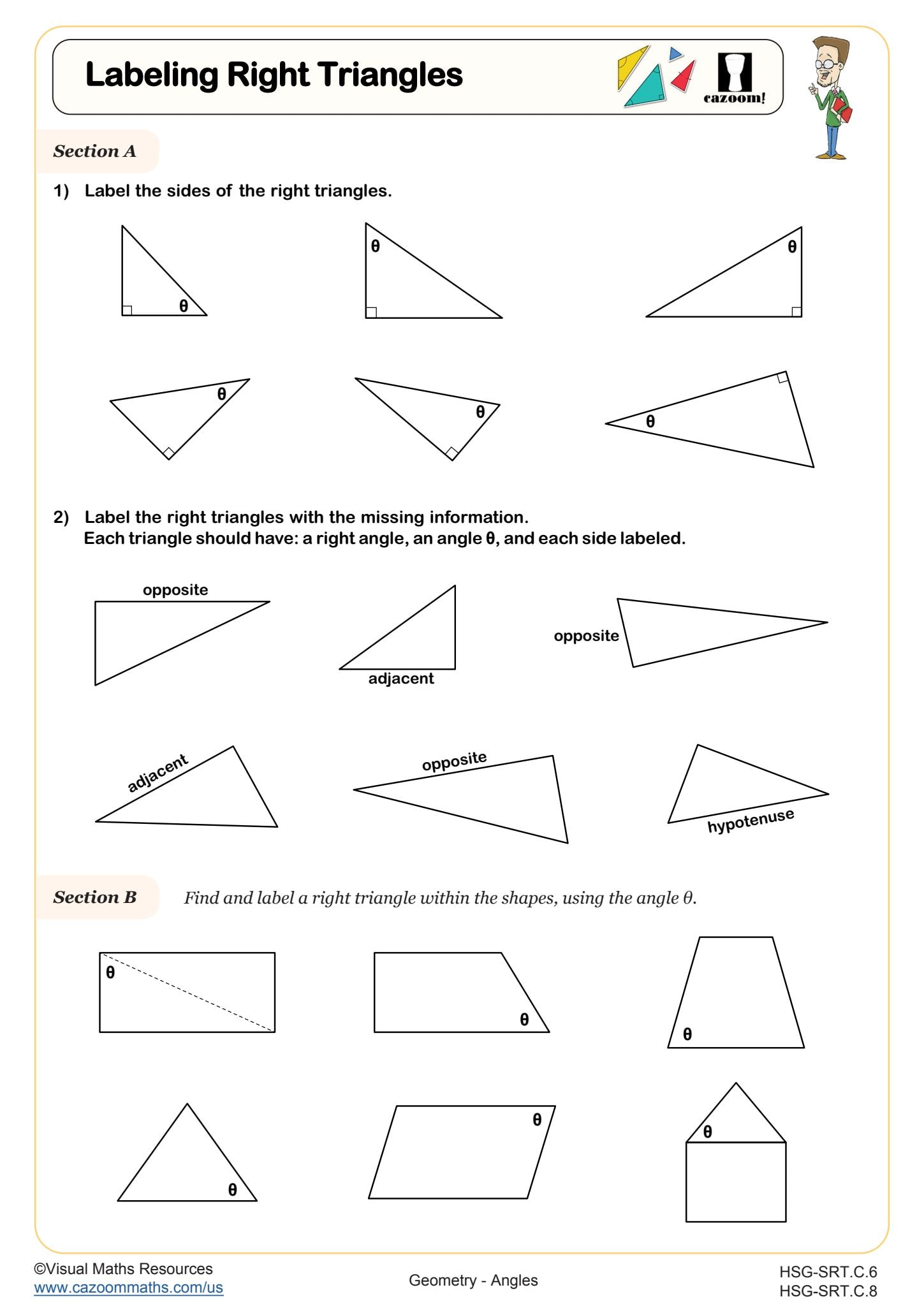
High school Geometry courses build on middle school foundations by emphasizing precise vocabulary for circle parts (radius, diameter, chord, secant, tangent, arc) and triangle components (hypotenuse, legs, opposite and adjacent sides). Students learn to identify these elements within diagrams and use proper terminology when writing proofs or explaining solution methods. The Common Core State Standards require students to understand how these properties connect to formulas, theorems, and geometric relationships.
A common mistake occurs when students label the hypotenuse as the side opposite the right angle rather than opposite to it. Teachers frequently observe this confusion on test problems involving the Pythagorean theorem or trigonometric ratios, where students correctly apply formulas but identify wrong side lengths. Students make significant progress when they practice with clearly labeled diagrams before moving to problems where they must determine labels independently.
How Do Standardized Tests Assess Knowledge of Shape Properties?
The SAT Math section and state Geometry assessments regularly include questions requiring students to identify shape components within complex diagrams or apply properties to solve multi-step problems. Test questions often embed circles within coordinate planes or present triangles in non-standard orientations, expecting students to recognize properties regardless of position. Students must quickly identify relevant parts, recall associated formulas, and execute calculations accurately under time pressure.
Students lose points when they misidentify components in rotated or reflected figures. For example, when a right triangle appears with the right angle at the top rather than bottom-left, students sometimes mislabel the hypotenuse because the orientation doesn't match their mental template. Similarly, circle problems involving multiple radii or chords challenge students who haven't practiced distinguishing these elements in layered diagrams. Timed practice with varied orientations builds the recognition speed standardized tests demand.
Why Is Accurate Triangle Labeling Critical for Trigonometry?
Labeling right triangles correctly establishes the foundation for trigonometric ratios (sine, cosine, tangent) that students encounter in both Geometry and Pre-Calculus. Students must identify the hypotenuse and then determine which leg is opposite and which is adjacent to a given acute angle. This labeling changes depending on the reference angle, requiring flexible thinking rather than memorization of fixed positions. Mastery of this skill prevents the most common trigonometry errors where students substitute incorrect side lengths into ratio formulas.
Engineers and architects use these principles when calculating structural angles, roof pitches, and load distributions. For instance, determining the length of roof rafters requires identifying the rise as the opposite side and the run as the adjacent side relative to the pitch angle. Students preparing for STEM fields benefit from recognizing that these labeling conventions aren't arbitrary classroom rules but standardized communication methods used across technical professions.
How Can Teachers Use These Worksheets in Geometry Classes?
These worksheets provide focused practice on vocabulary and component identification before students tackle theorem applications and proofs. The structured format allows students to build confidence with basic labeling before progressing to problems where they must determine which properties apply. Teachers can use the answer keys to create worked examples on the board, demonstrating proper notation and common pitfalls. The clear diagrams help students develop the visual recognition skills needed for success on assessments.
Many teachers assign these worksheets as warm-up activities before introducing the Pythagorean theorem, trigonometric ratios, or circle theorems. They work well for intervention with students who struggle on test questions despite understanding formulas, as the issue often traces back to component identification rather than calculation skills. The worksheets also support paired work where students explain their labeling choices to partners, reinforcing vocabulary through discussion. Teachers frequently use them as reference sheets during unit reviews, helping students refresh terminology before comprehensive exams.