Geometry Ratio Worksheets
What Do Geometry Ratio Worksheets Cover?
Geometry ratio worksheets focus on proportional relationships within geometric contexts, including direct proportion, scale factors, and ratios in coordinate systems. Students work with problems that require setting up and solving proportions to find missing side lengths, coordinate values, and measurements in similar figures. The worksheets align with Common Core standards for high school geometry that emphasize understanding similarity through proportional reasoning.
A common error teachers observe is students writing ratios in inconsistent order, such as comparing width to height in one ratio but height to width in another. This mistake becomes particularly problematic when working with coordinates or determining scale factors, where maintaining consistent ratio structure determines whether students arrive at correct answers. The worksheets provide practice identifying corresponding parts and establishing proper ratio notation before solving.
How Do Ratios Appear on the SAT and ACT?
Standardized tests like the SAT and ACT frequently include ratio problems embedded within geometry questions, particularly those involving similar triangles, scale drawings, and coordinate geometry. Students must demonstrate they can set up proportions correctly, cross-multiply to solve for unknowns, and apply ratio concepts to find distances, areas, or coordinates. These questions often appear in both calculator and no-calculator sections, requiring fluency with proportion mechanics.
Students lose points when they fail to recognize that area ratios relate to the square of linear scale factors, not the scale factor itself. For example, if two similar figures have a side ratio of 2:3, many students incorrectly assume the area ratio is also 2:3 rather than 4:9. This misconception costs points on multiple-choice questions where answer choices deliberately include the linear ratio as a distractor.
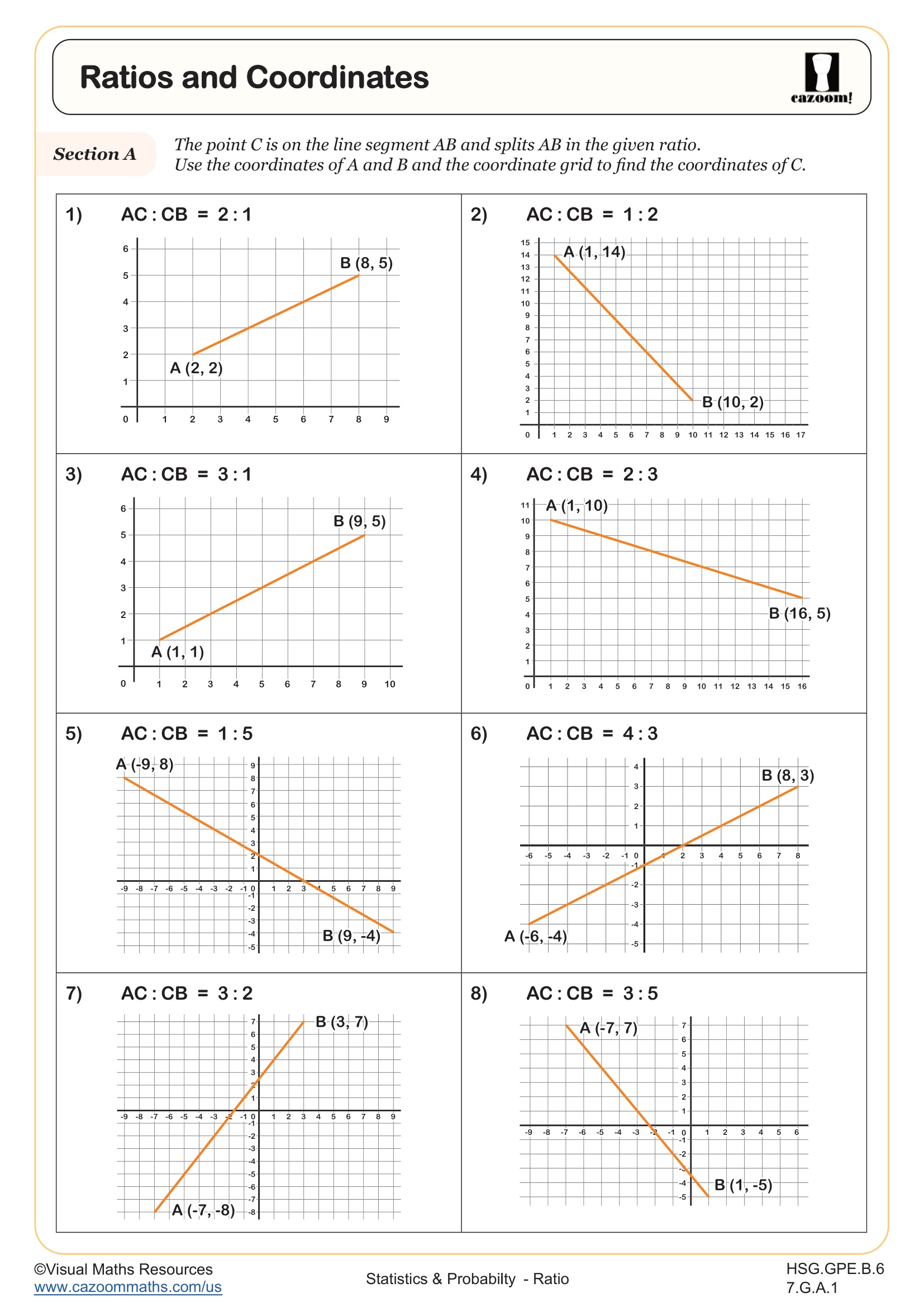
What Is Direct Proportion and Why Does It Matter?
Direct proportion describes relationships where two quantities maintain a constant ratio, meaning as one value increases, the other increases proportionally. In geometry, students encounter direct proportion when working with similar figures, where corresponding sides maintain constant ratios, or in coordinate geometry when points divide line segments in specific ratios. Understanding that y = kx represents direct proportion helps students recognize these relationships algebraically and graphically.
Direct proportion appears throughout STEM fields, from architectural scale drawings to engineering stress-strain relationships. Architects use proportional reasoning to create scaled floor plans where every measurement maintains the same ratio to actual dimensions. In physics, Hooke's Law demonstrates direct proportion between force and spring displacement, while chemistry students use proportional relationships in solution dilution calculations. College-bound students benefit from recognizing that proportional reasoning underlies dimensional analysis and unit conversion across scientific disciplines.
How Can Teachers Use These Ratio Worksheets Effectively in Geometry?
These worksheets provide structured practice that builds from basic ratio setup through more complex applications in coordinate geometry and proportional relationships. The progression helps students develop confidence with proportion notation before applying these skills to geometric contexts. Teachers can use the answer keys to quickly identify whether errors stem from calculation mistakes or fundamental misunderstandings about setting up equivalent ratios.
Many teachers assign these worksheets as warm-up activities before introducing similarity theorems or as review before state assessments that test proportional reasoning. The direct proportion problems work well for paired activities where one student sets up the proportion while their partner solves it, encouraging discussion about ratio structure. The coordinate ratio problems serve as effective preparation for section formulas and distance applications that appear later in analytic geometry units.