Geometry Similarity and Congruence Worksheets
What concepts do similarity and congruence worksheets cover in Geometry?
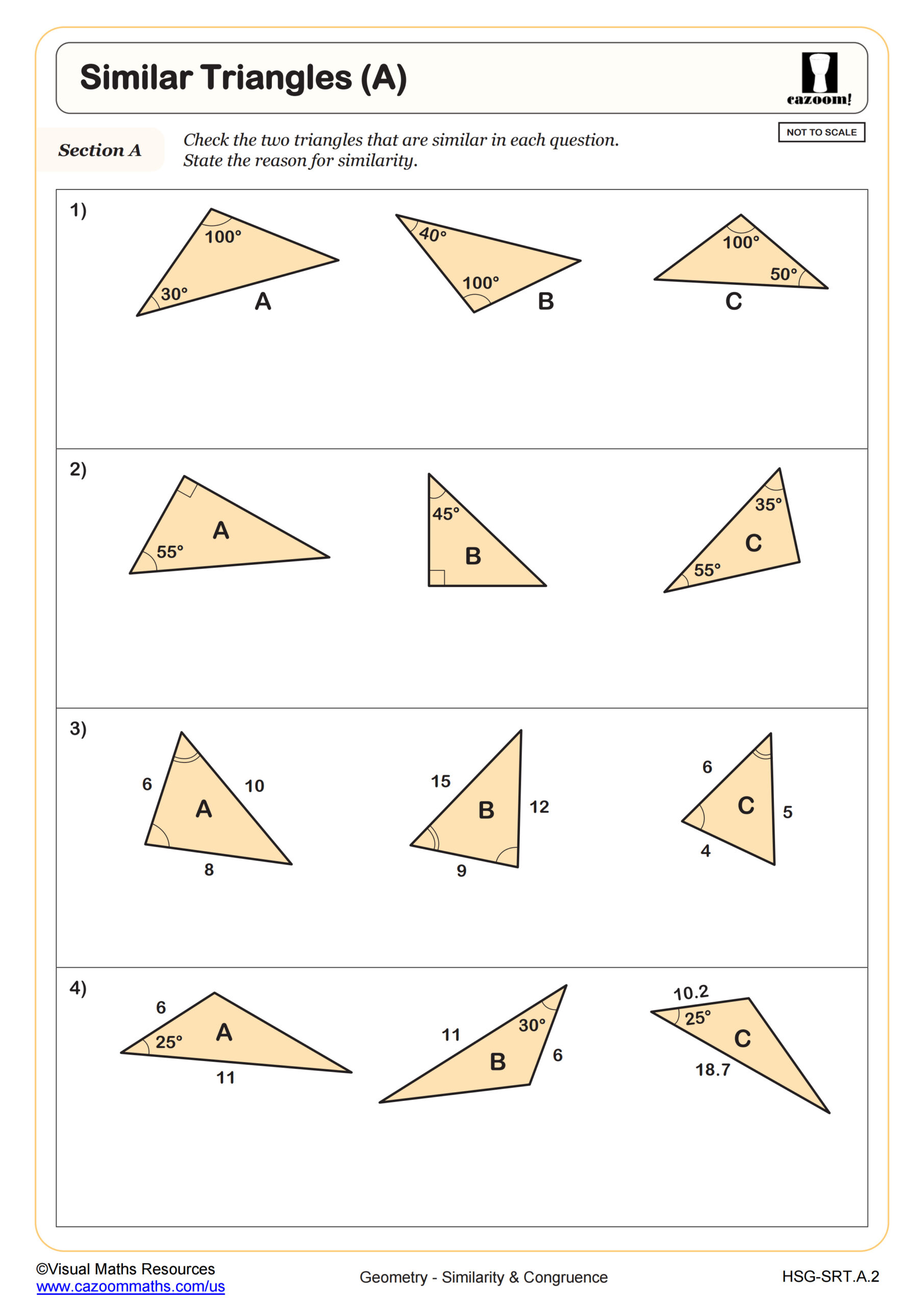
Similarity and congruence worksheets address Common Core standards for transformations and geometric reasoning in high school Geometry. Students work with congruence criteria (SSS, SAS, ASA, AAS, HL), similarity theorems (AA, SAS, SSS), and apply these principles to prove relationships between figures. The worksheets include problems involving scale factors, corresponding parts of similar triangles, and proportional reasoning with both two-dimensional and three-dimensional figures.
Students often lose points on tests when they write correct similarity statements but fail to set up proportions with corresponding sides in the proper order. Teachers notice this error persists until students develop a consistent method for labeling vertices and matching corresponding parts systematically. Practice with identifying corresponding angles and sides before setting up equations helps students avoid this common pitfall, particularly when working with figures in different orientations.
How do standardized tests assess similarity and congruence?
The SAT and ACT regularly test similarity and congruence through multi-step problems that combine proportional reasoning with area or volume calculations. Students must demonstrate understanding of triangle similarity theorems, apply scale factors correctly, and recognize that area scales by the square of the linear scale factor while volume scales by the cube. State assessments typically require students to write formal proofs showing figures are similar or congruent using geometric postulates and theorems.
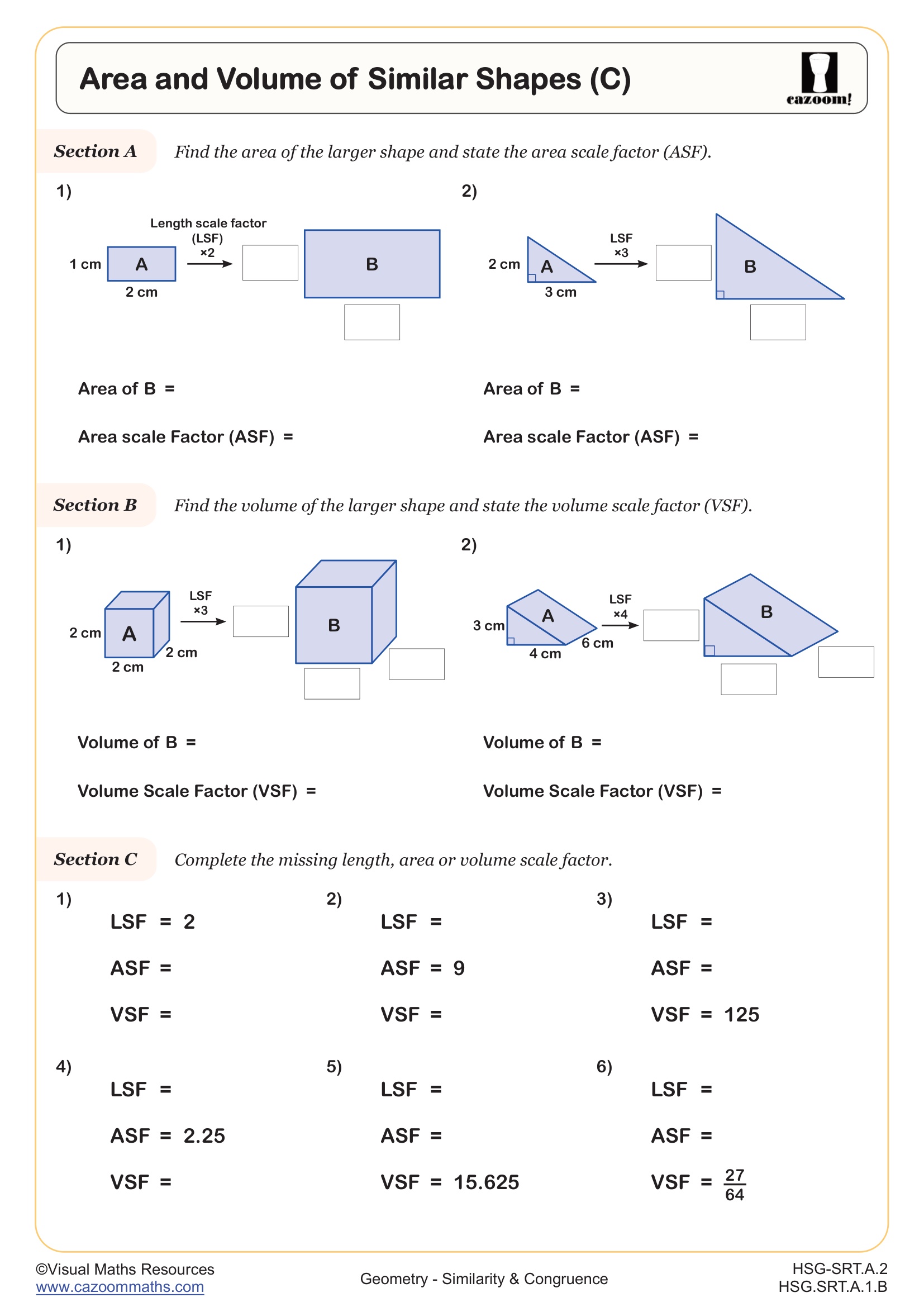
A common error on standardized tests occurs when students correctly identify a scale factor of 2 but then multiply the original area by 2 instead of 4. Students lose valuable points by forgetting that doubling dimensions quadruples area and multiplies volume by eight. Questions involving indirect measurement or shadow problems also appear frequently, requiring students to set up and solve proportions based on similar triangles in real-world contexts.
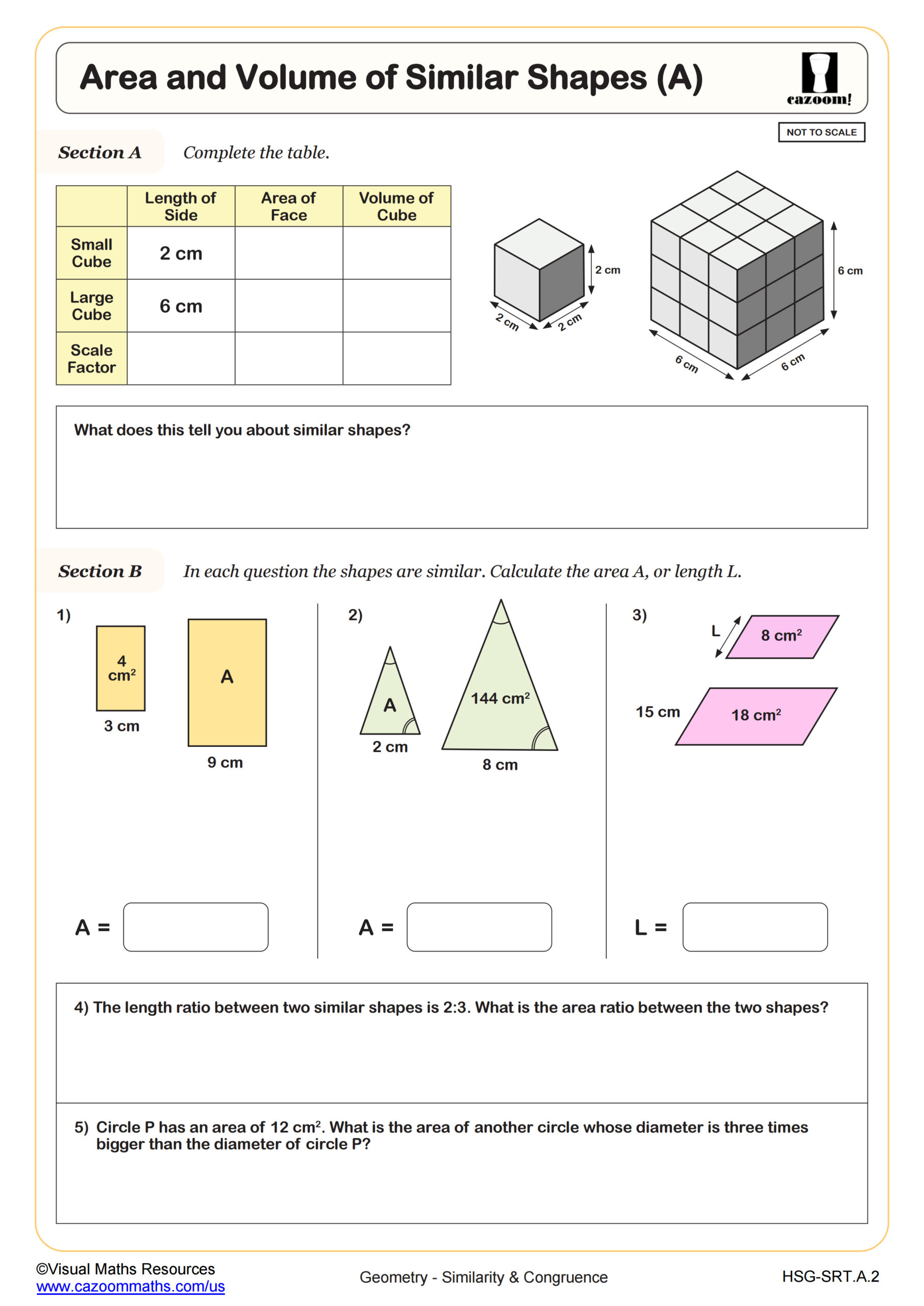
How do similar figures relate to area and volume calculations?
When two figures are similar with a scale factor of k, their corresponding lengths are in the ratio k:1, their areas are in the ratio k²:1, and their volumes are in the ratio k³:1. Students must recognize these relationships to solve problems efficiently rather than recalculating every measurement individually. For example, if two similar cylinders have a height ratio of 3:1, their volumes will have a ratio of 27:1 without needing to compute both volumes separately using the cylinder formula.
This concept appears throughout STEM applications, from architectural scale models to pharmaceutical manufacturing. Engineers use similarity principles when scaling prototypes to full-size structures, knowing that material costs increase by the square of linear dimensions while structural loads increase by the cube. Chemistry students encounter these relationships when comparing reaction rates in containers of different sizes, where surface area to volume ratios affect reaction speed and heat distribution.
How can teachers use these similarity and congruence worksheets effectively?
These worksheets provide scaffolded practice that builds from identifying congruent and similar figures to applying scale factors in complex area and volume problems. Teachers can use the varying difficulty levels to differentiate instruction, assigning foundational worksheets for students still developing proportional reasoning skills while challenging advanced students with multi-step applications. The answer keys allow students to check their work during independent practice, helping them identify conceptual errors before assessments.
Many teachers use these worksheets for targeted review before unit tests or as intervention materials when students struggle with scale factor applications. The worksheets work well for paired practice, where one student solves while another checks the solution process against the answer key, promoting mathematical discourse about problem-solving strategies. Teachers also assign specific worksheets for homework after introducing AA similarity or when students need additional practice connecting geometric similarity to algebraic proportion-solving before state assessments.