Geometry Solving Equations Worksheets
What Do Geometry Solving Equations Worksheets Cover?
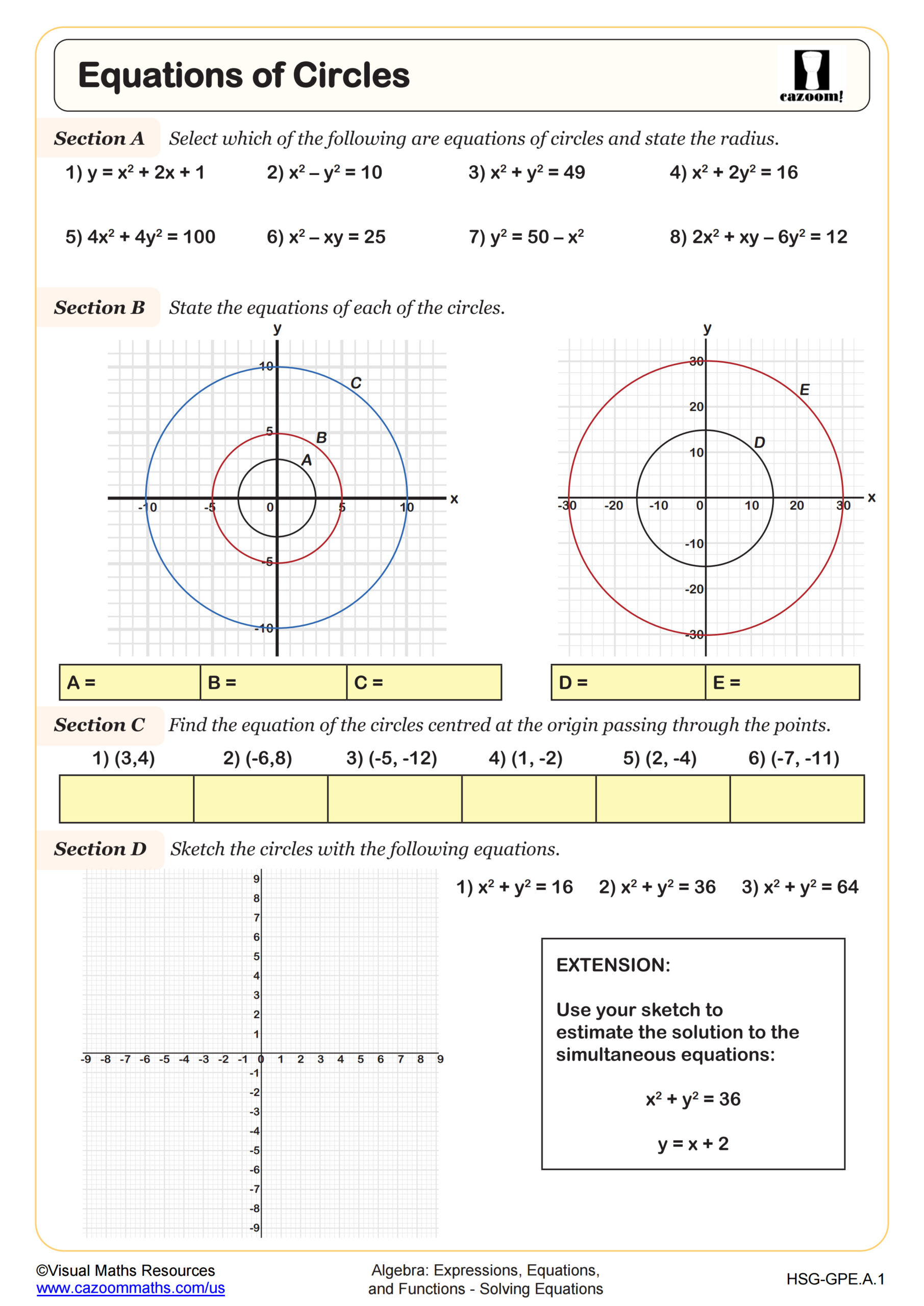
These worksheets address the algebraic side of coordinate geometry, focusing on writing equations for circles using the standard form (x-h)²+(y-k)²=r² and deriving equations for lines tangent to circles. Students apply the distance formula, perpendicular slope relationships, and point-slope form within geometric contexts that appear throughout the Common Core State Standards for high school geometry.
Many teachers observe that students initially treat these as purely algebraic exercises without recognizing the geometric meaning behind each step. A common error occurs when students correctly find the center and radius of a circle but then substitute values incorrectly into the standard form equation. The breakthrough typically happens when students sketch the circle and tangent line first, visualizing why the radius to the point of tangency must be perpendicular to the tangent line.
How Do Solving Equations Appear on Standardized Tests?
The SAT and ACT regularly include questions involving circle equations in coordinate geometry, often requiring students to identify centers and radii or determine whether a point lies on, inside, or outside a circle. State assessments expect students to move fluidly between geometric descriptions and algebraic representations, demonstrating understanding of how equations model geometric objects.
Students lose points when they fail to complete the square correctly to convert general form equations to standard form, or when they forget that the standard form uses (x-h)² rather than (x+h)². Another frequent error involves sign mistakes when working with negative coordinates for the center. Standardized tests also assess whether students recognize that tangent lines are perpendicular to radii, a conceptual understanding that requires both geometric intuition and algebraic execution.
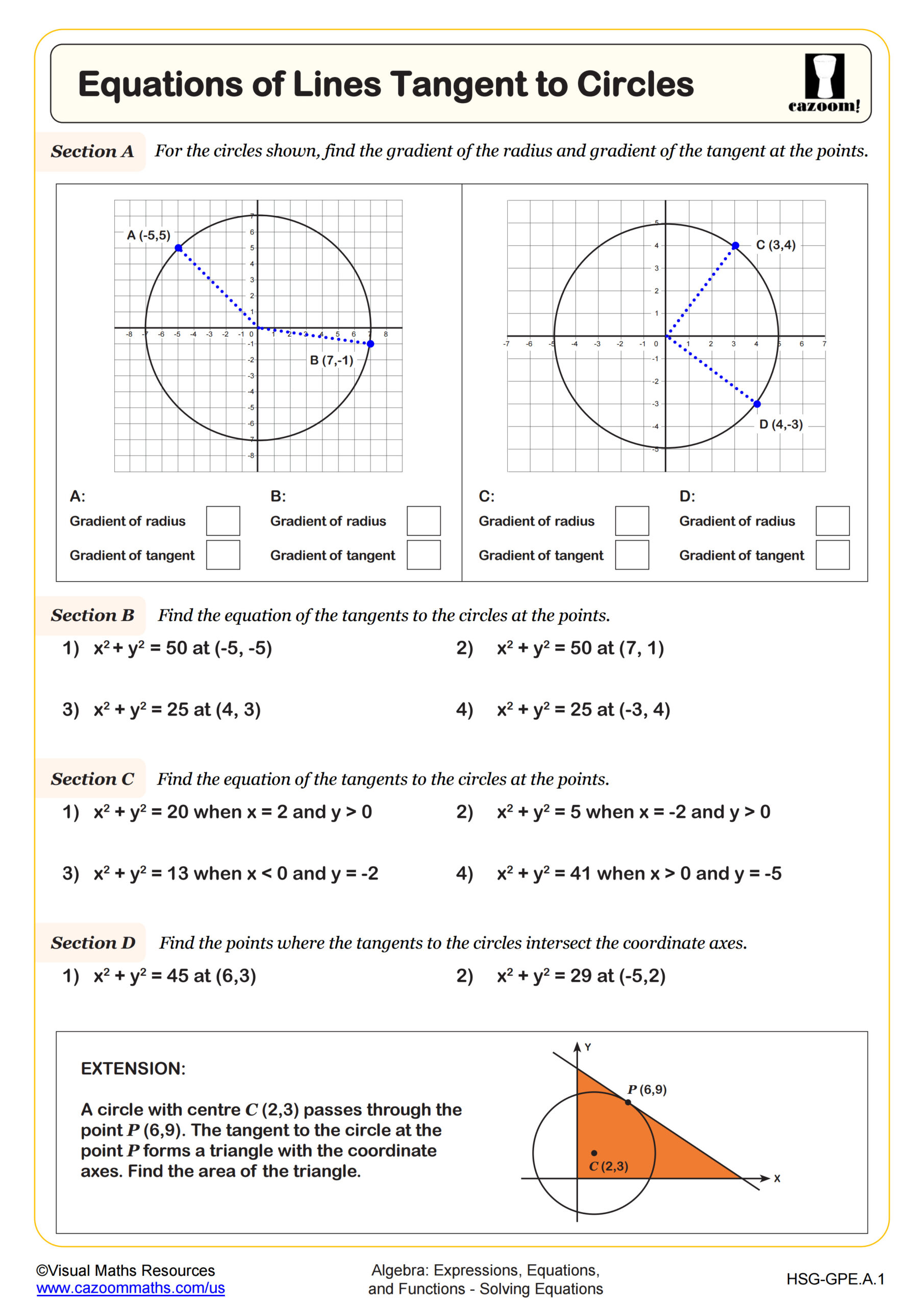
How Do Students Find Equations of Tangent Lines to Circles?
Finding the equation of a tangent line to a circle requires students to recognize that the radius drawn to the point of tangency is perpendicular to the tangent line. Students first locate the center of the circle, then find the slope of the radius connecting the center to the point of tangency. The tangent line's slope is the negative reciprocal of this radius slope, which students then use with point-slope form to write the tangent line equation.
This skill appears in computer graphics and animation, where programmers must calculate tangent lines to create smooth curves and realistic motion paths. Engineering applications include determining optimal angles for ramps or supports that must touch circular structures at specific points. College-bound STEM students encounter these concepts again in calculus when finding tangent lines to any curve, making the geometric foundation valuable for future coursework.
How Can Teachers Use These Geometry Worksheets Effectively?
The worksheets provide structured practice that moves students from identifying circle properties to constructing complete equations. Answer keys allow students to check their work immediately, helping them identify where algebraic errors occur in multi-step problems. Teachers find that having worked solutions helps students recognize patterns in the problem-solving process, particularly the consistent sequence of finding the center, calculating slopes, and applying perpendicularity.
Many teachers use these worksheets for targeted intervention with students who struggle on coordinate geometry test questions or as focused review before unit assessments. The problems work well for paired problem-solving, where one student focuses on the geometric relationships while the other handles algebraic manipulation. Teachers also assign these as homework before introducing more complex applications, ensuring students have solid equation-writing skills before tackling circle-line intersection problems or optimizing distances in coordinate plane scenarios.