Geometry Trigonometry Worksheets
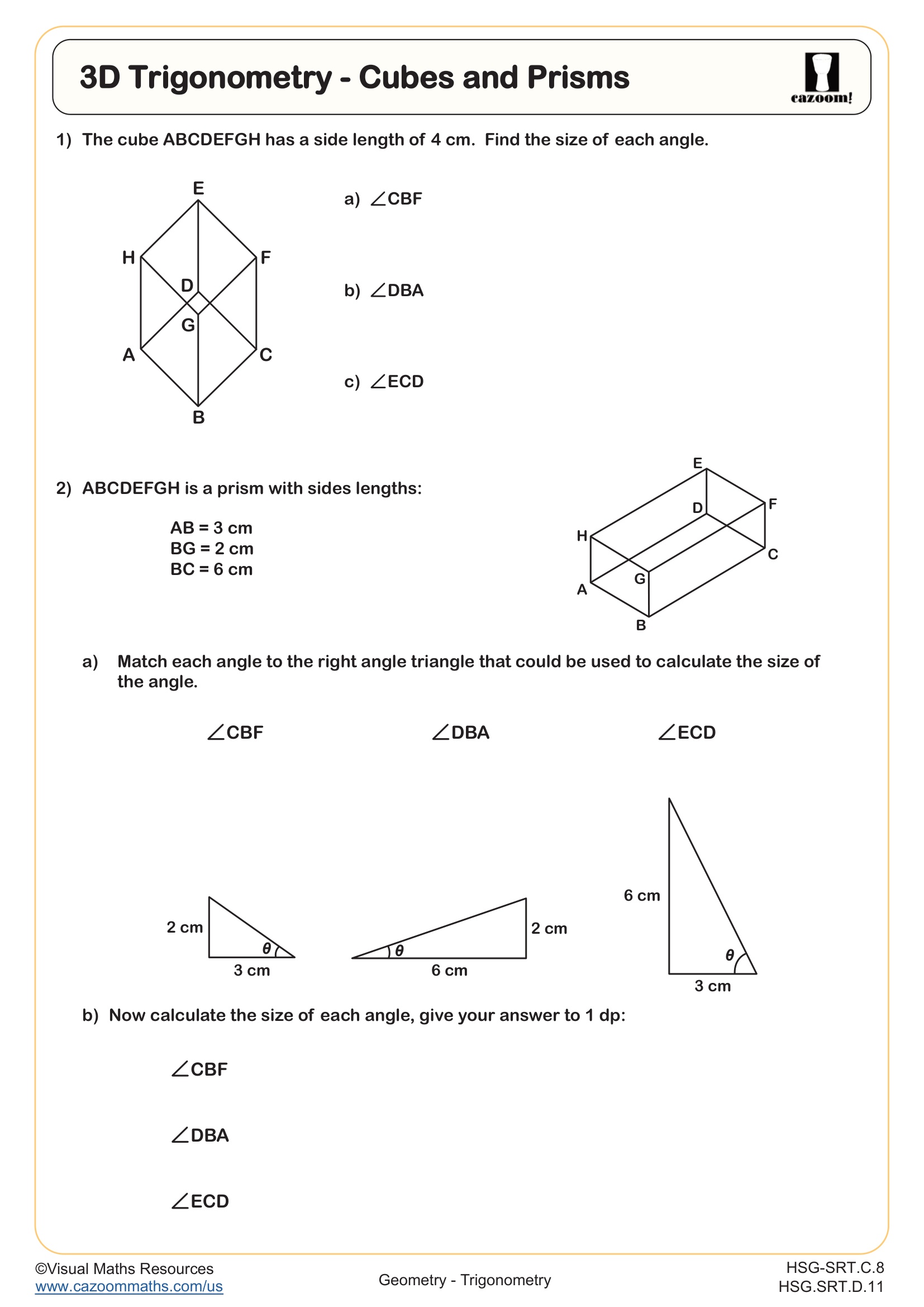
3D Trigonometry - Cubes and Prisms
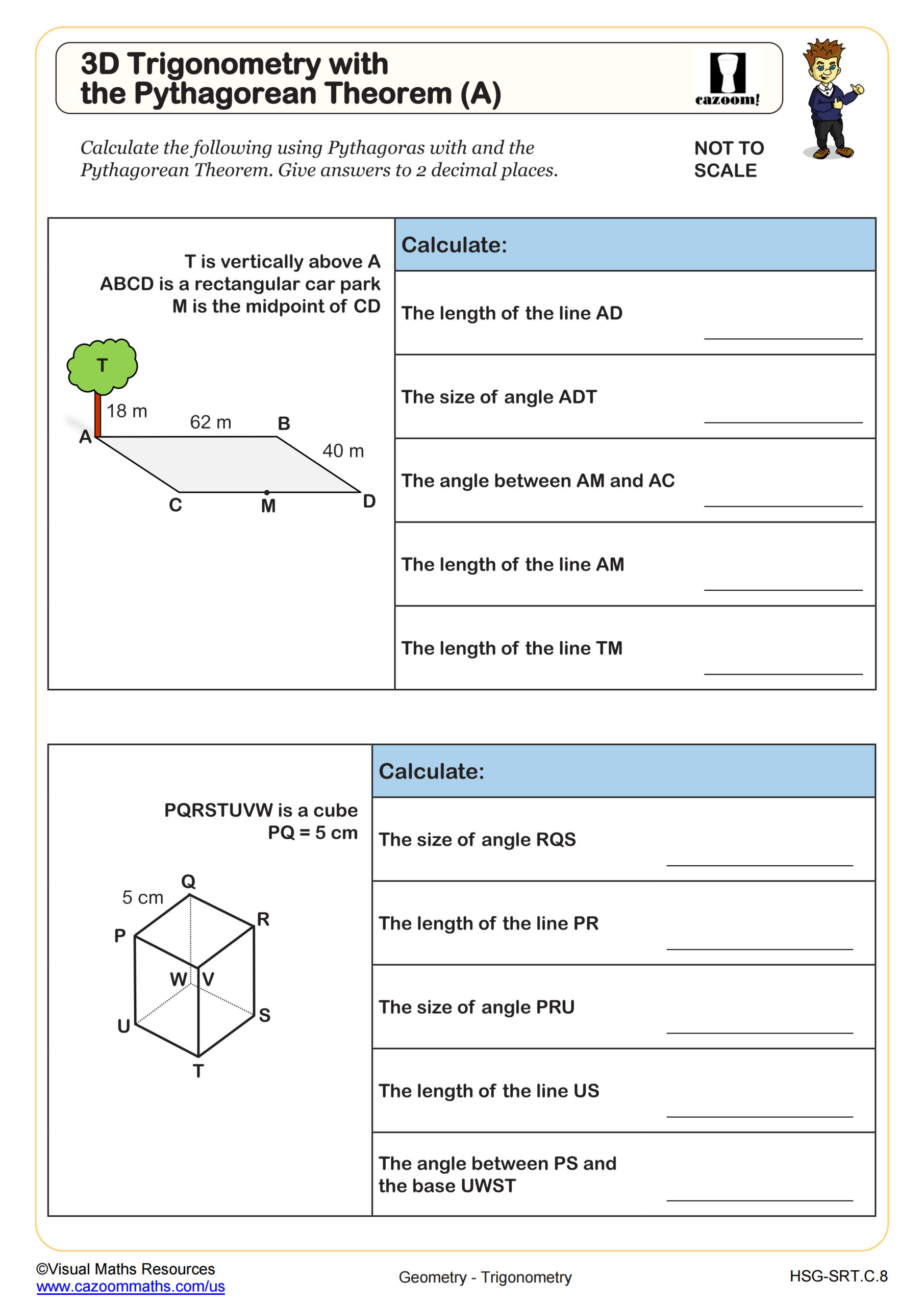
3D Trigonometry with the Pythagorean Theorem (A)
3D Trigonometry with the Pythagorean Theorem (B)

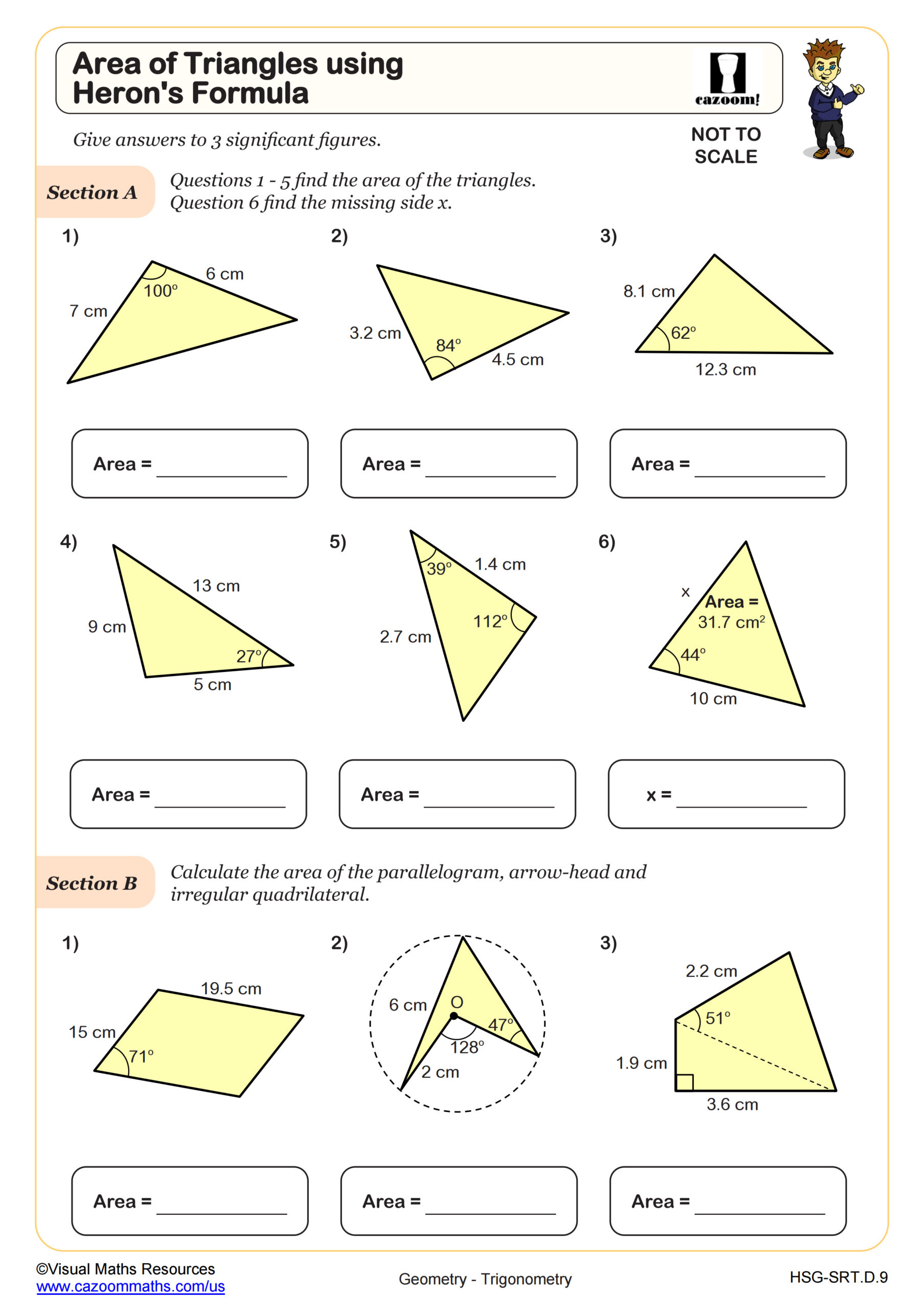
Area of Triangles using Heron's Formula
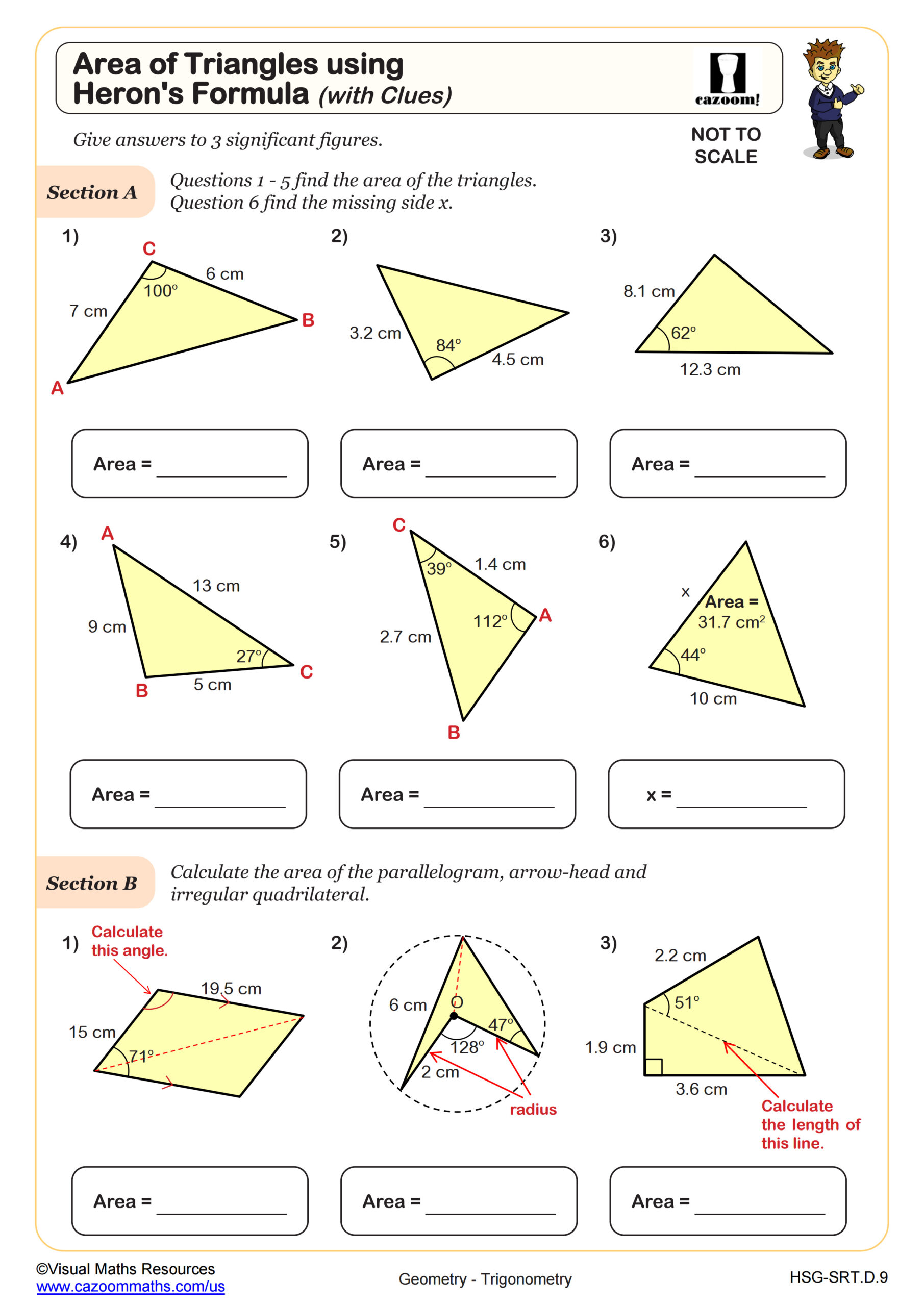
Area of Triangles using Heron's Formula (with clues)
Choosing the Correct Trig Rule

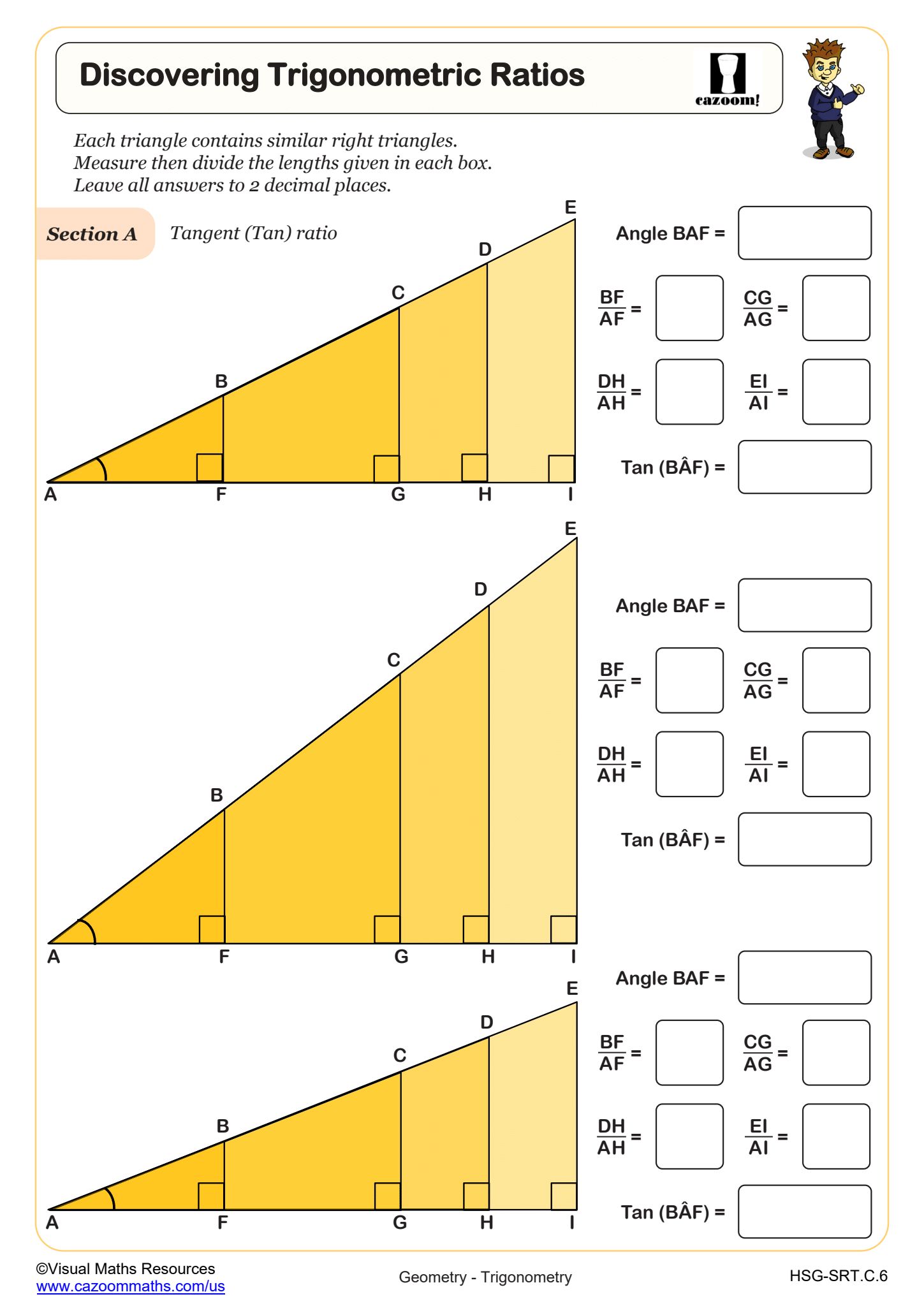
Discovering Trigonometric Ratios
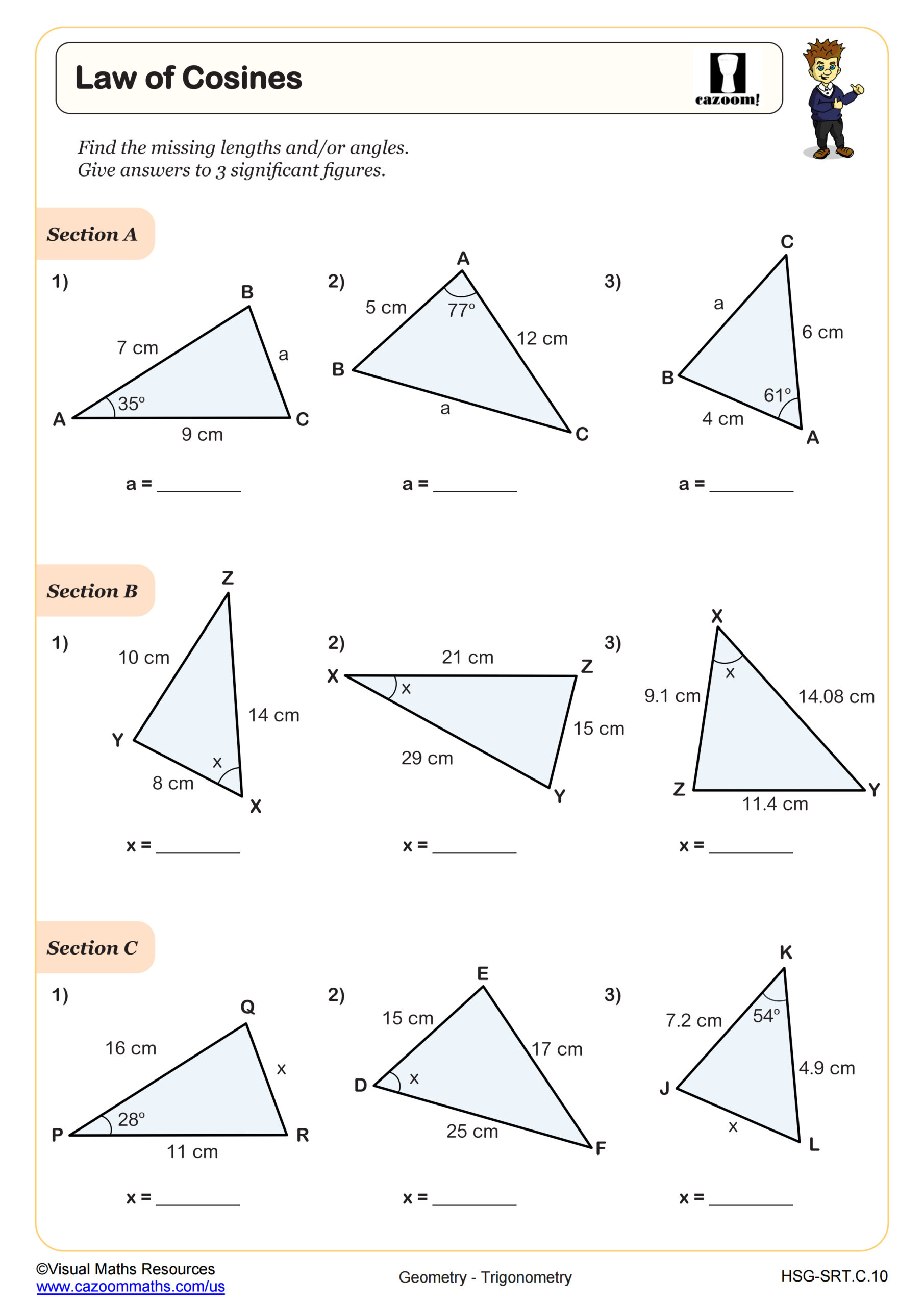
Law of Cosines
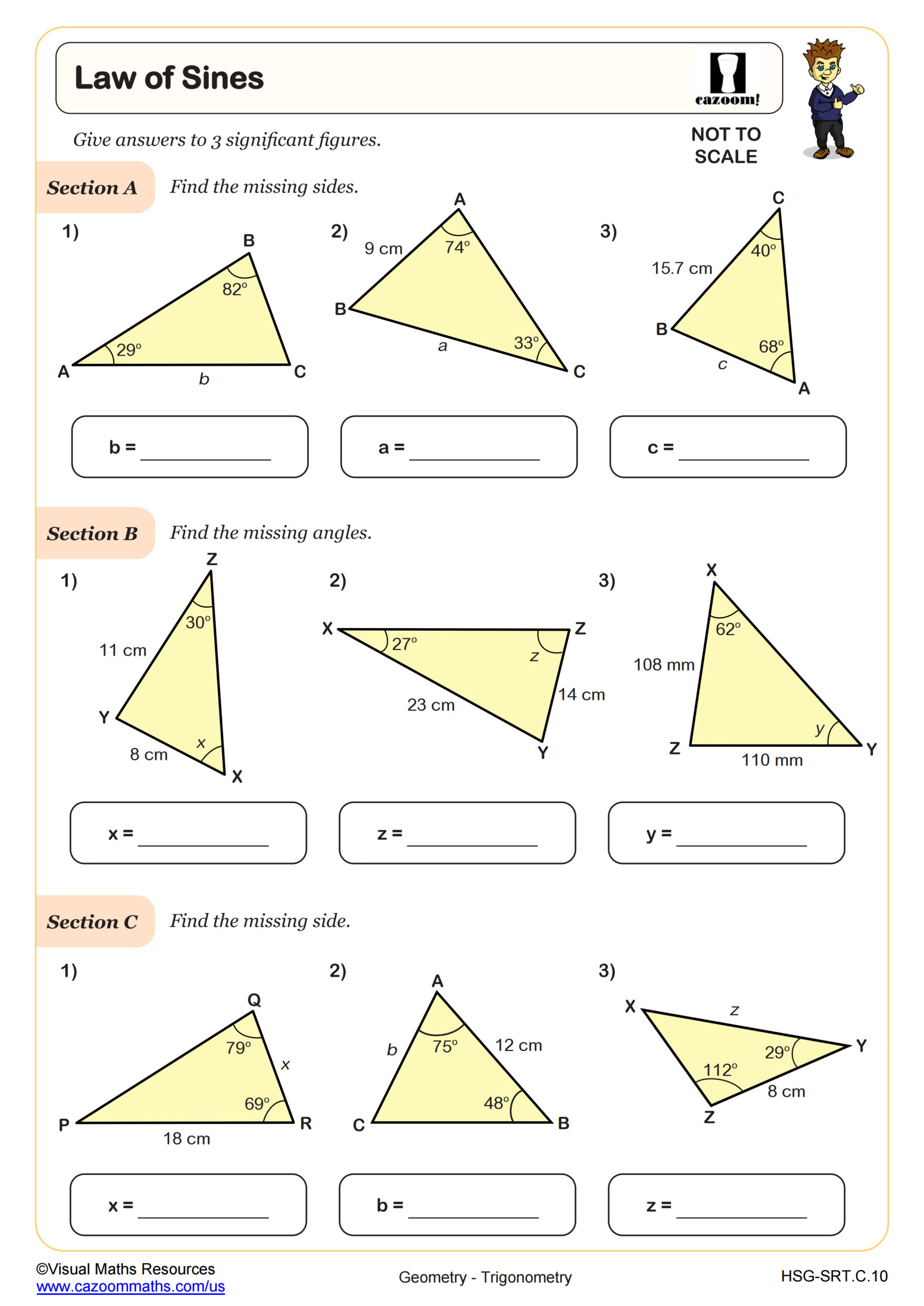
Law of Sines
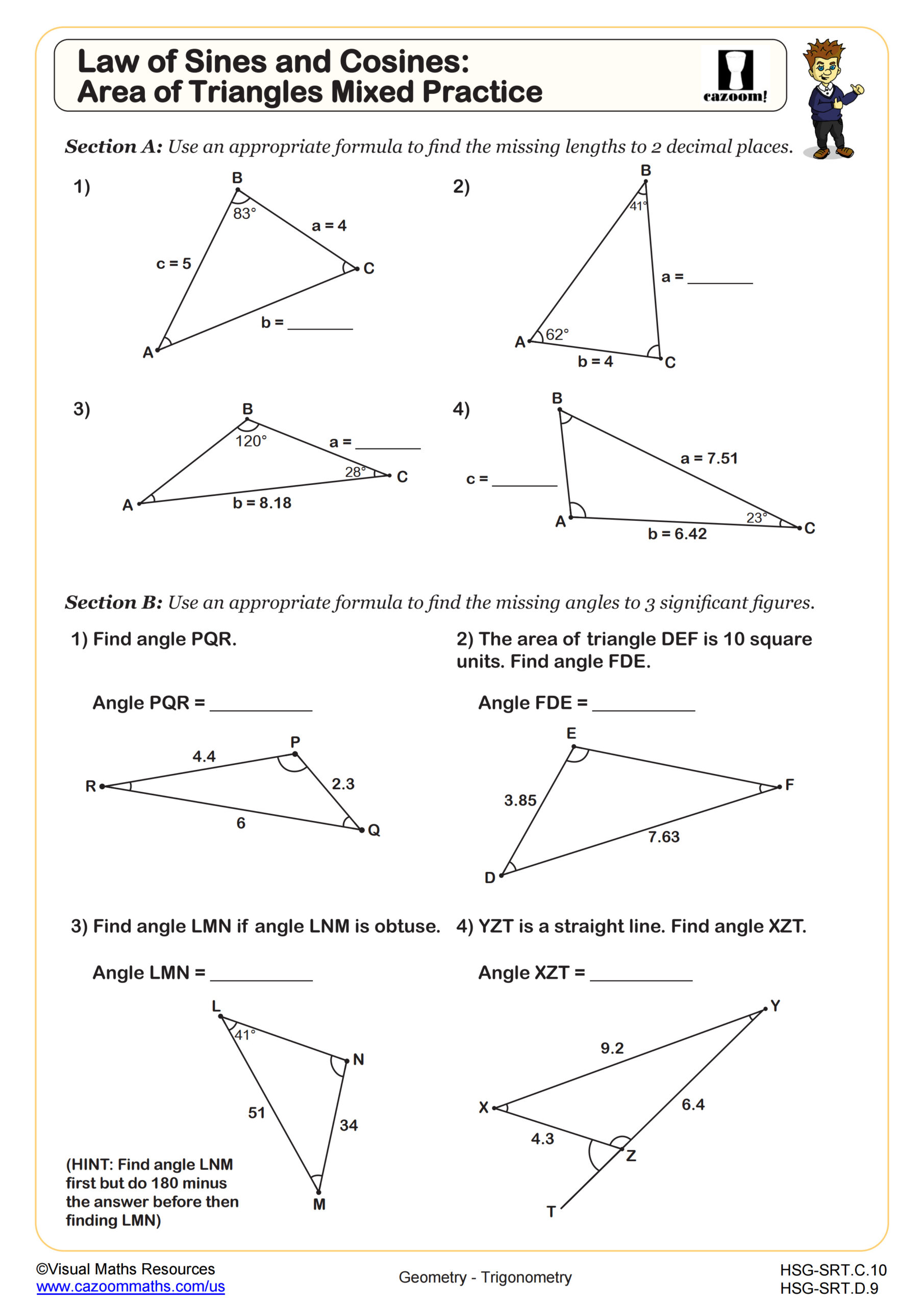
Law of Sines and Cosines; Area of Triangles Mixed Practice
Proving Values of Special Right Triangles

Pythagorean Thereom or Trigonometry? (A)
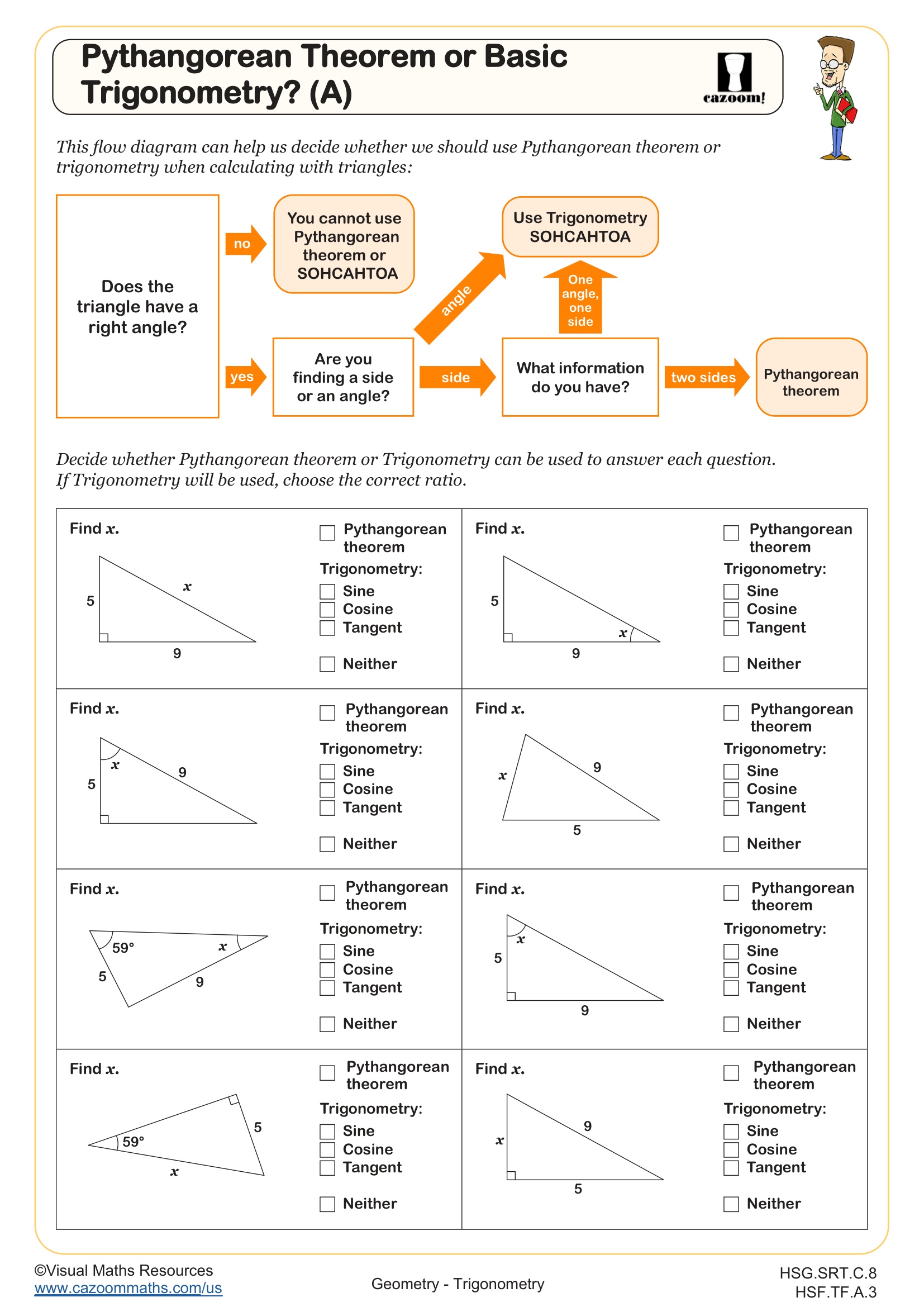
Pythagorean Thereom or Trigonometry? (B)
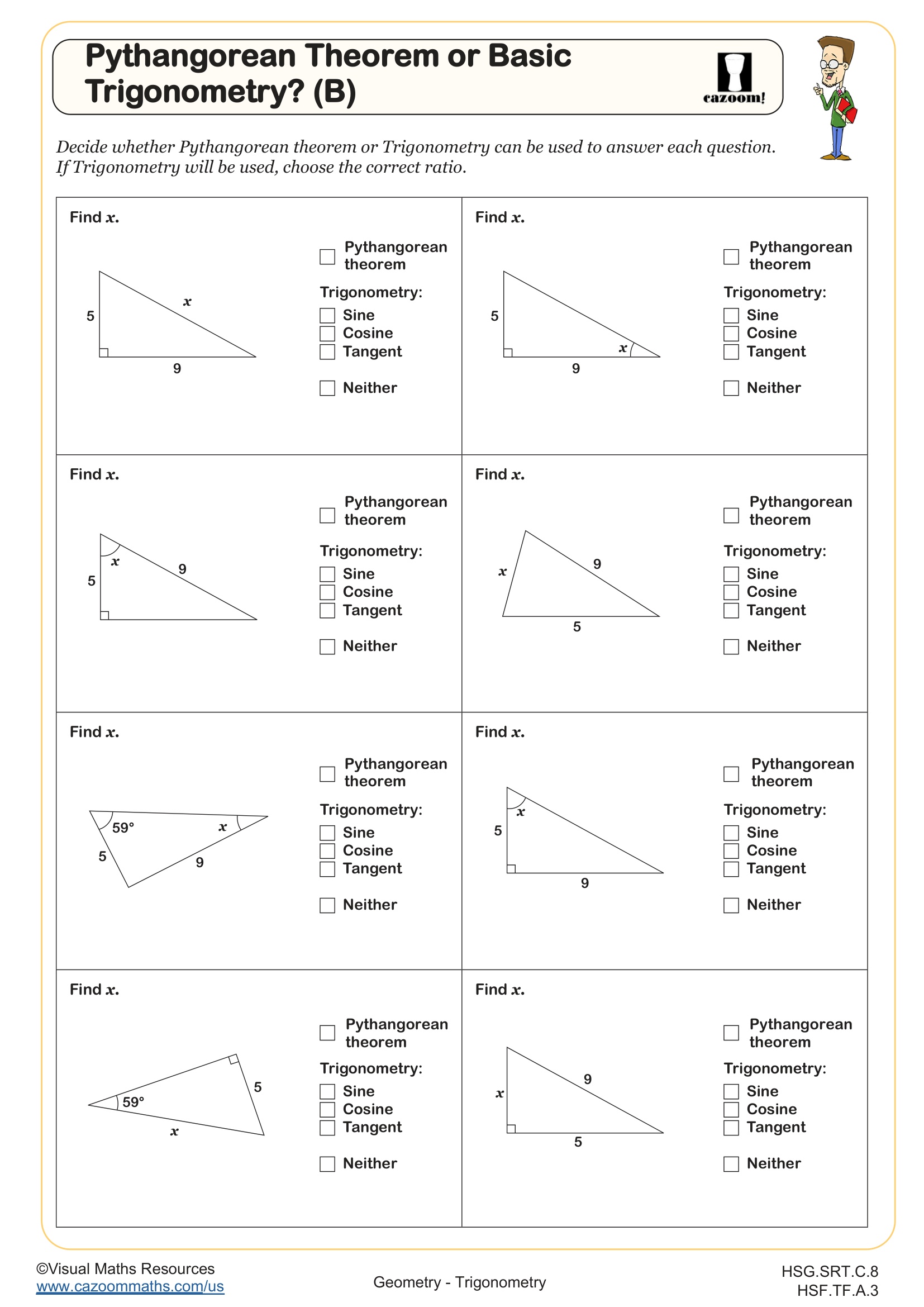
The Cosine Rule - Finding Angles
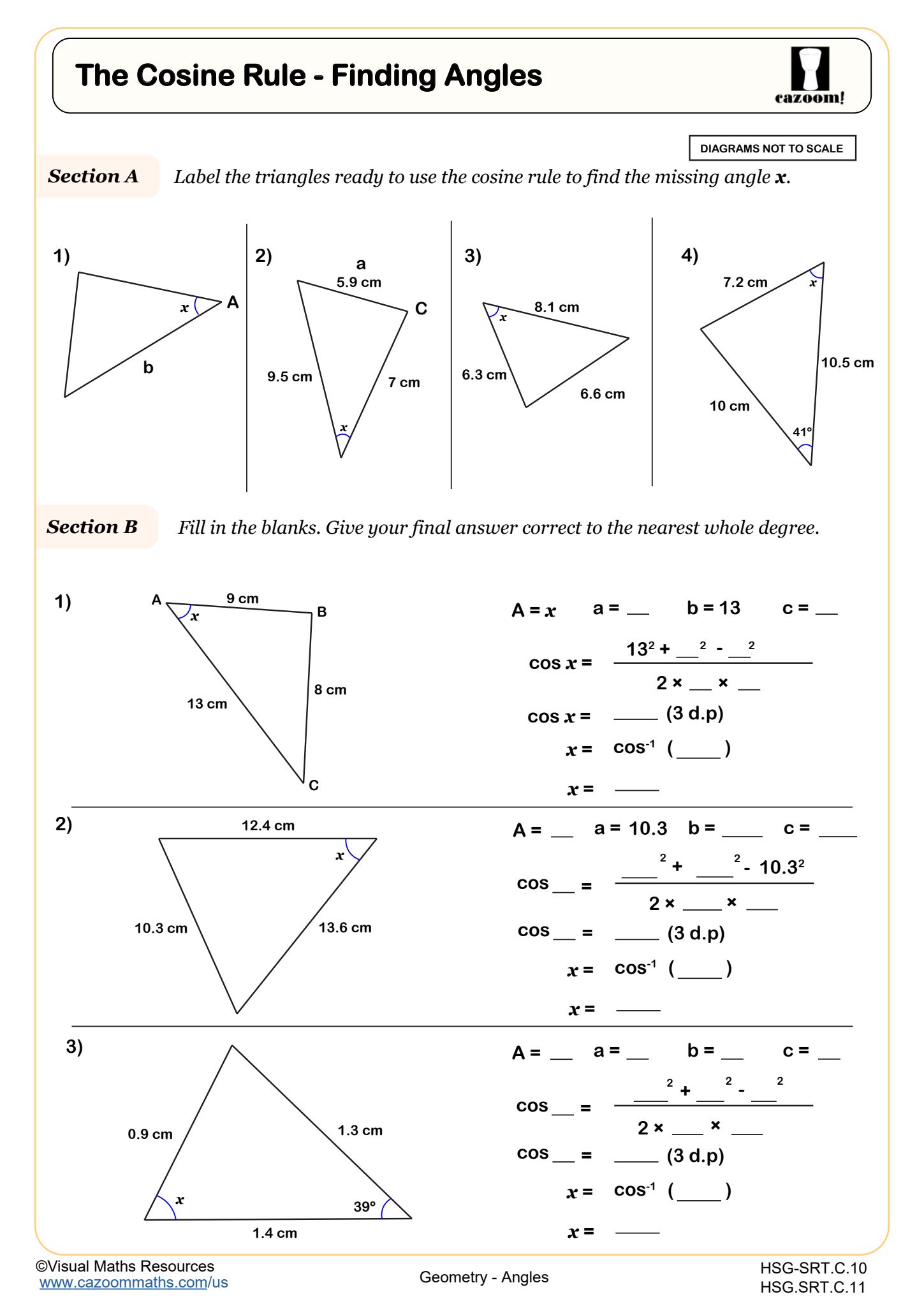
The Cosine Rule - Finding Lengths
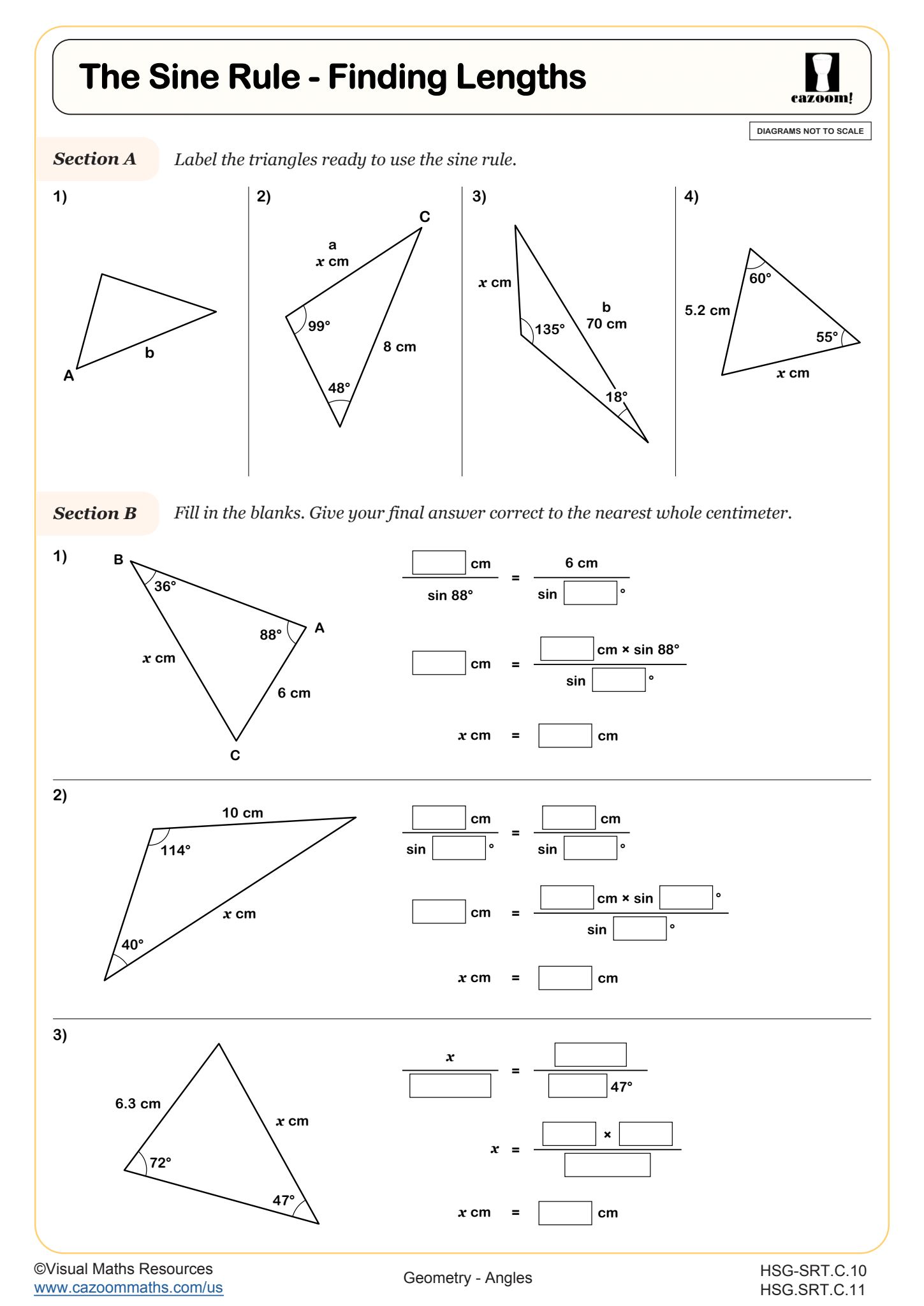
The Sine Rule - Finding Lengths
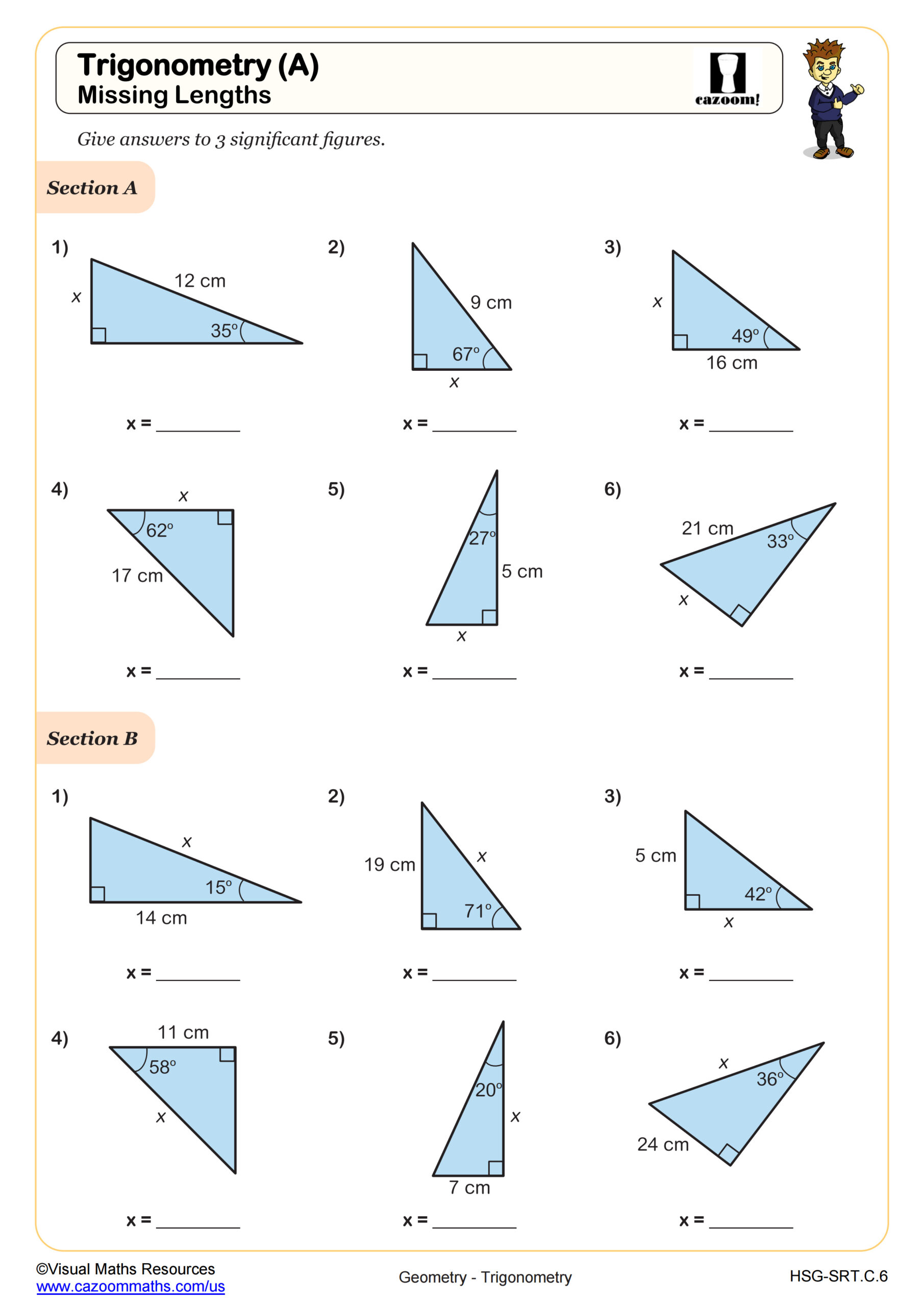
Trigonometic Ratios (SOH CAH TOA): Missing Side Lengths
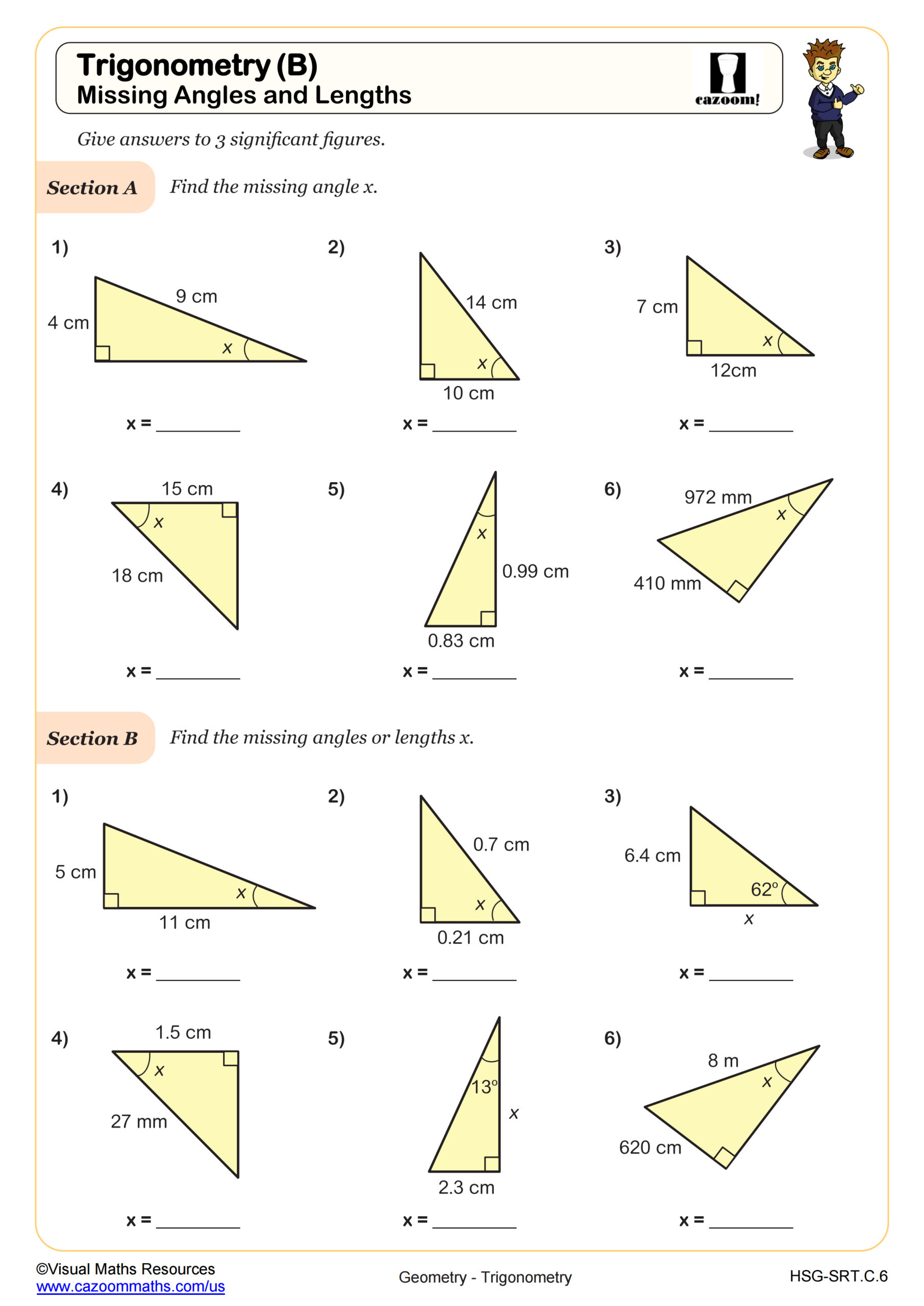
Trigonometic Ratios (SOH CAH TOA): Word Problems

Trigonometic Ratios (SOH CAH TOA): Word Problems (With Clues)

Trigonometric Ratios: Missing Side Lengths and Angle Measures
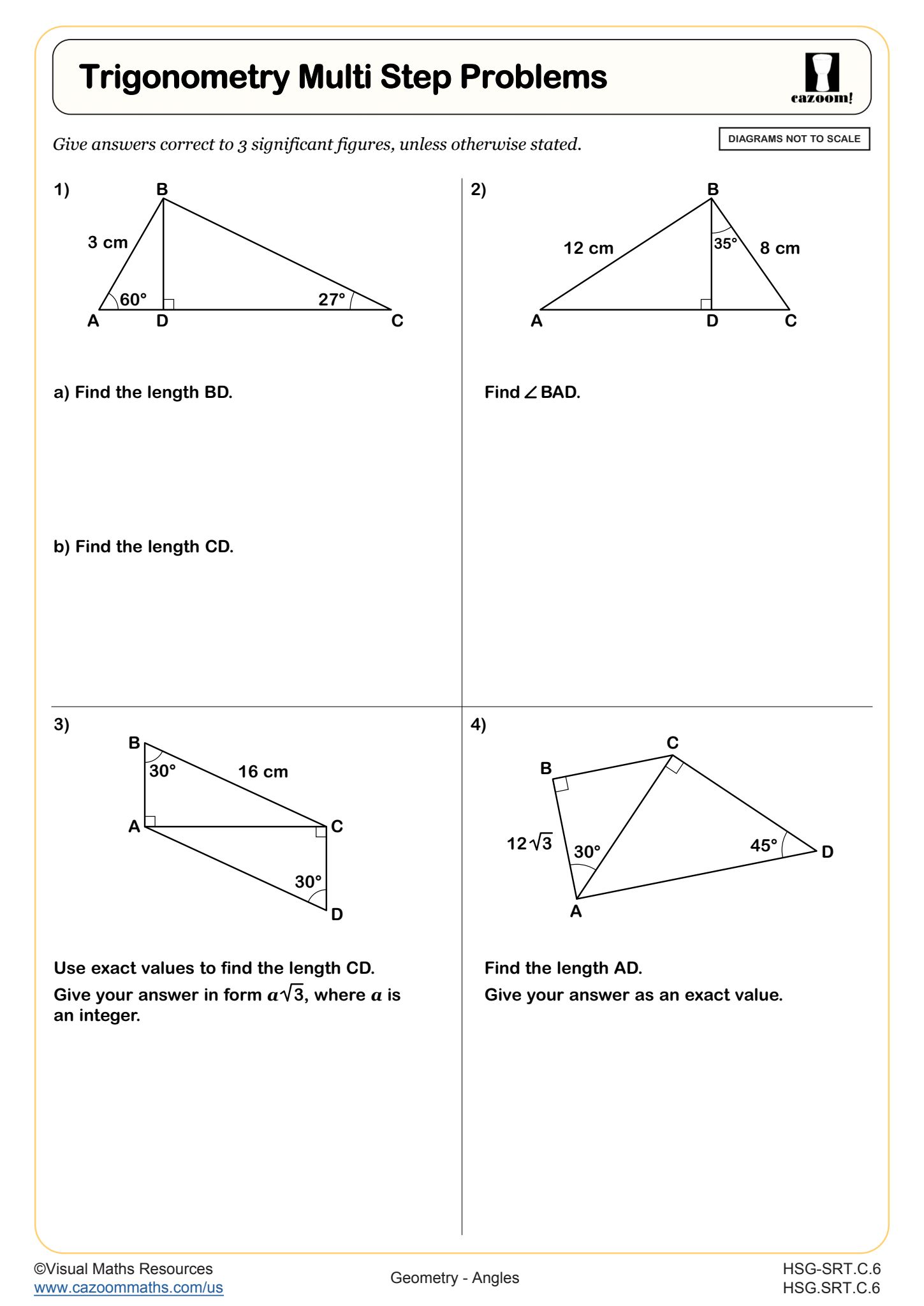
Trigonometry Multi Step Problems
Using Special Right Triangles

What Trigonometry Concepts Are Covered in High School Geometry?
Geometry trigonometry focuses on right triangle trigonometry (sine, cosine, tangent ratios), special right triangles (30-60-90 and 45-45-90), the Pythagorean theorem, Law of Sines, Law of Cosines, and triangle area formulas including Heron's formula. These topics align with Common Core standards for high school Geometry and establish the foundation students need before advancing to Algebra II or Precalculus trigonometry, where they'll study the unit circle and trigonometric functions more deeply.
Students frequently confuse when to apply the Pythagorean theorem versus trigonometric ratios. Teachers notice this confusion especially on mixed practice worksheets where students must first identify whether they have a right triangle before choosing a solution method. The Law of Sines and Cosines extend trigonometry beyond right triangles, which represents a significant conceptual shift that requires deliberate practice with non-right triangle diagrams.
How Does Trigonometry Appear on the SAT and State Math Assessments?
Standardized tests like the SAT include trigonometry questions that test students' ability to apply sine, cosine, and tangent ratios in context, solve for missing sides or angles in triangles, and interpret trigonometric relationships in word problems or diagrams. The ACT math section dedicates approximately four questions to trigonometry, including questions about special right triangles and basic trigonometric identities. State assessments aligned with Common Core standards expect students to model with trigonometry and explain their reasoning when choosing solution methods.
Students lose points when they fail to check whether their calculator is in degree or radian mode, a mistake that produces wildly incorrect answers. Another common error occurs when students apply the Law of Sines to situations requiring the Law of Cosines, particularly when given two sides and the included angle (SAS). Teachers notice that students who regularly practice identifying which formula applies before solving perform significantly better on timed assessments.
What Makes the Law of Cosines Different from the Law of Sines?
The Law of Cosines works for any triangle when students know either two sides and the included angle (SAS) or all three sides (SSS), making it particularly useful when the Law of Sines creates ambiguous cases or isn't applicable. The formula c² = a² + b² - 2ab cos(C) extends the Pythagorean theorem to non-right triangles, and students often recognize this connection once they see that when the angle is 90 degrees, the cosine term drops out. The Law of Sines, meanwhile, relates sides to their opposite angles and works best with AAS, ASA, or SSA triangle information.
Civil engineers and surveyors use the Law of Cosines to calculate distances when direct measurement isn't possible, such as determining property boundaries on irregular terrain or measuring distances across bodies of water. Navigation systems rely on these calculations to triangulate position, and architects apply the Law of Cosines when designing roof trusses or structural supports where angles and lengths must be precisely determined for load-bearing calculations.
How Can Teachers Use These Trigonometry Worksheets in Geometry Class?
These worksheets provide scaffolded practice that progresses from basic right triangle trigonometry through more complex applications involving non-right triangles and mixed problem sets. The answer keys allow students to self-check during independent practice or homework, helping them identify specific areas where they need additional support before assessments. Teachers find the variety of problem types helpful for differentiation, as students can work on worksheets matched to their current skill level while building toward more challenging applications.
Many teachers assign specific worksheets for targeted test preparation, particularly before unit exams or state assessments when students need focused review on weak areas. The mixed practice worksheets work well for station activities where students rotate through different problem types, or as bell ringers that activate prior knowledge before introducing related concepts. Some teachers use these worksheets for paired problem-solving, where students explain their reasoning to partners, which surfaces misconceptions more effectively than silent independent work.