Integrated Math 1 Algebra Worksheets
Algebra Multiplication Pyramids (A)
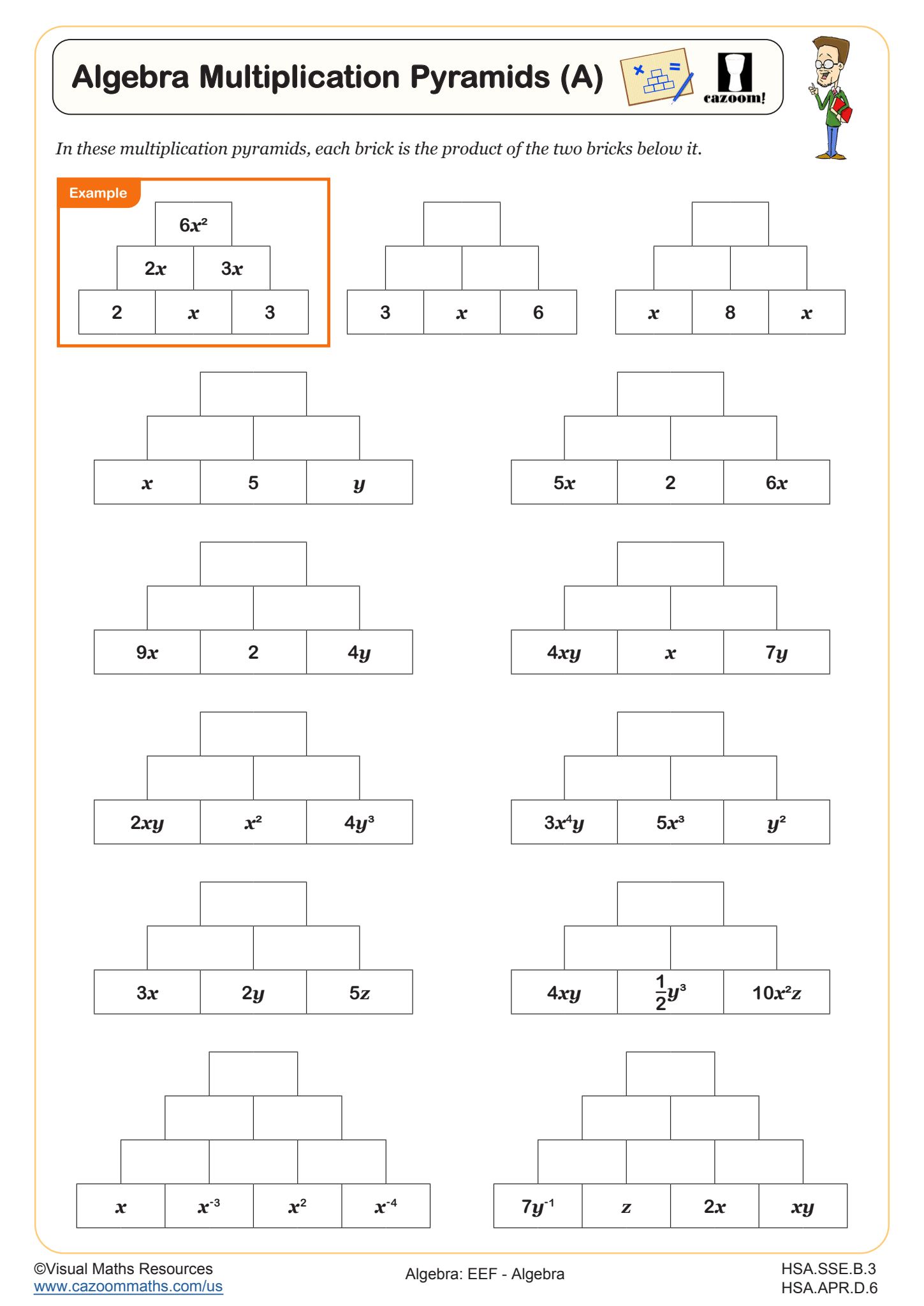
Algebra Multiplication Pyramids (B)
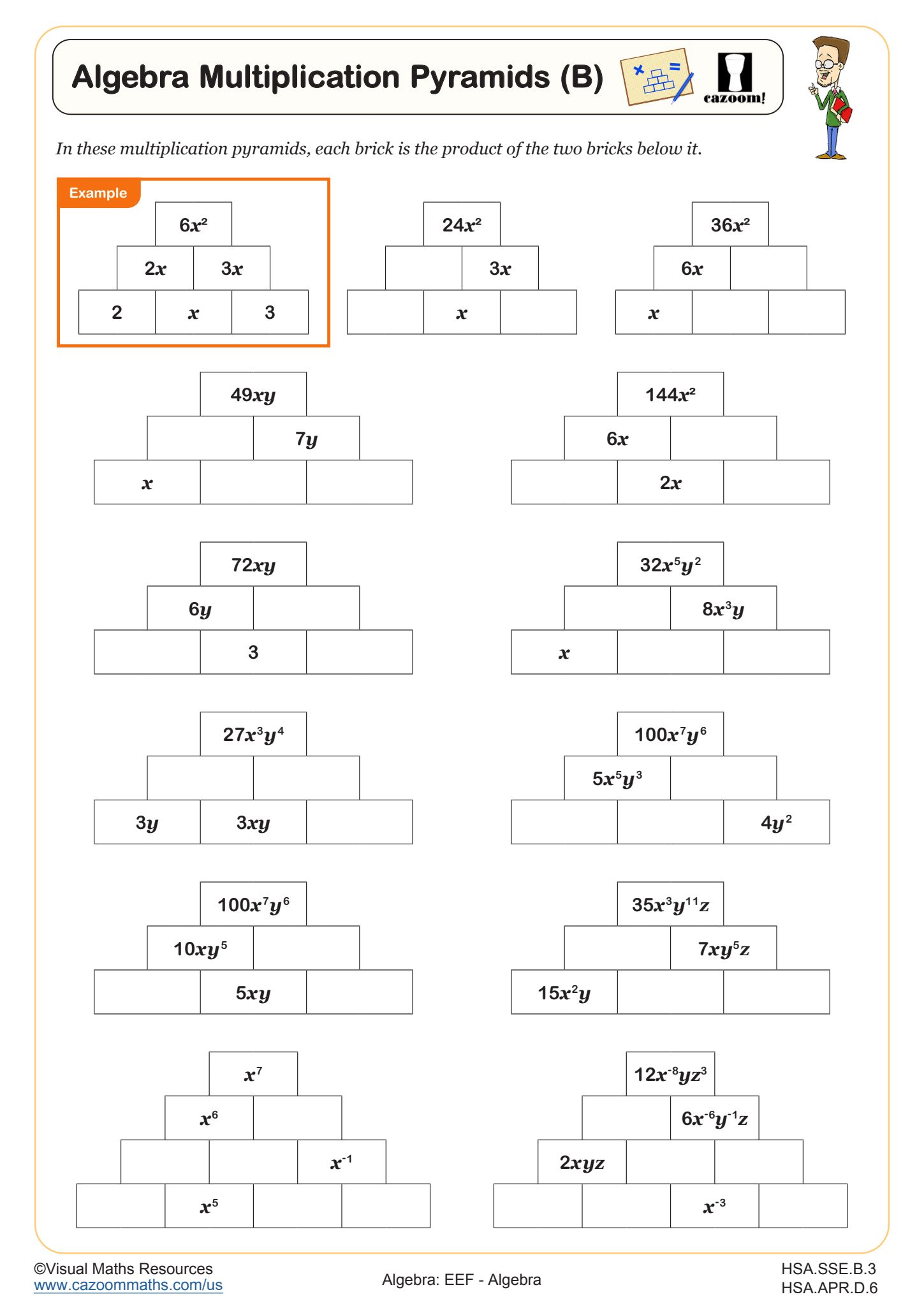
Changing the Subject: Requires Factorization
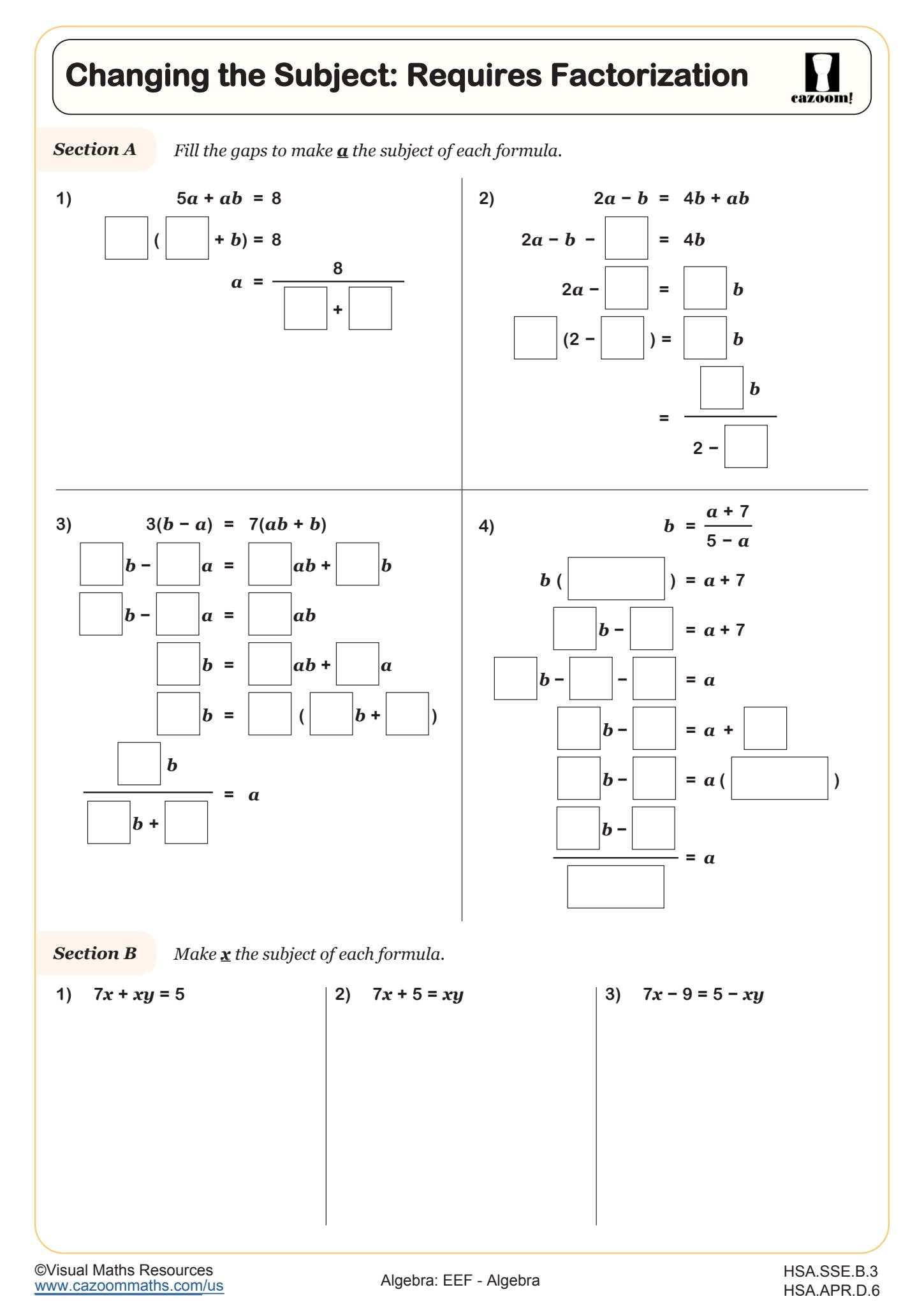
Finding Slope (A)
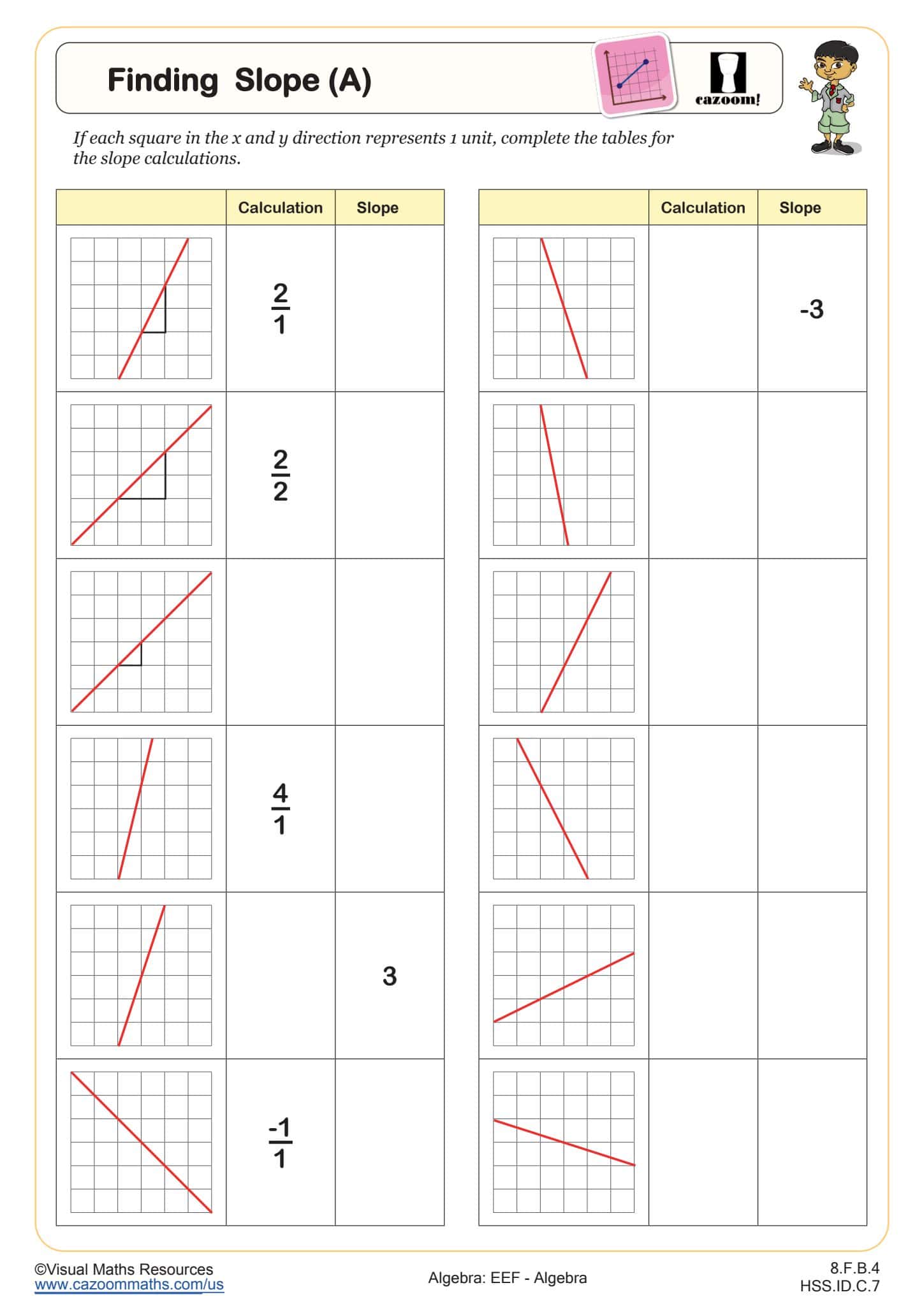
Finding Slope (B)
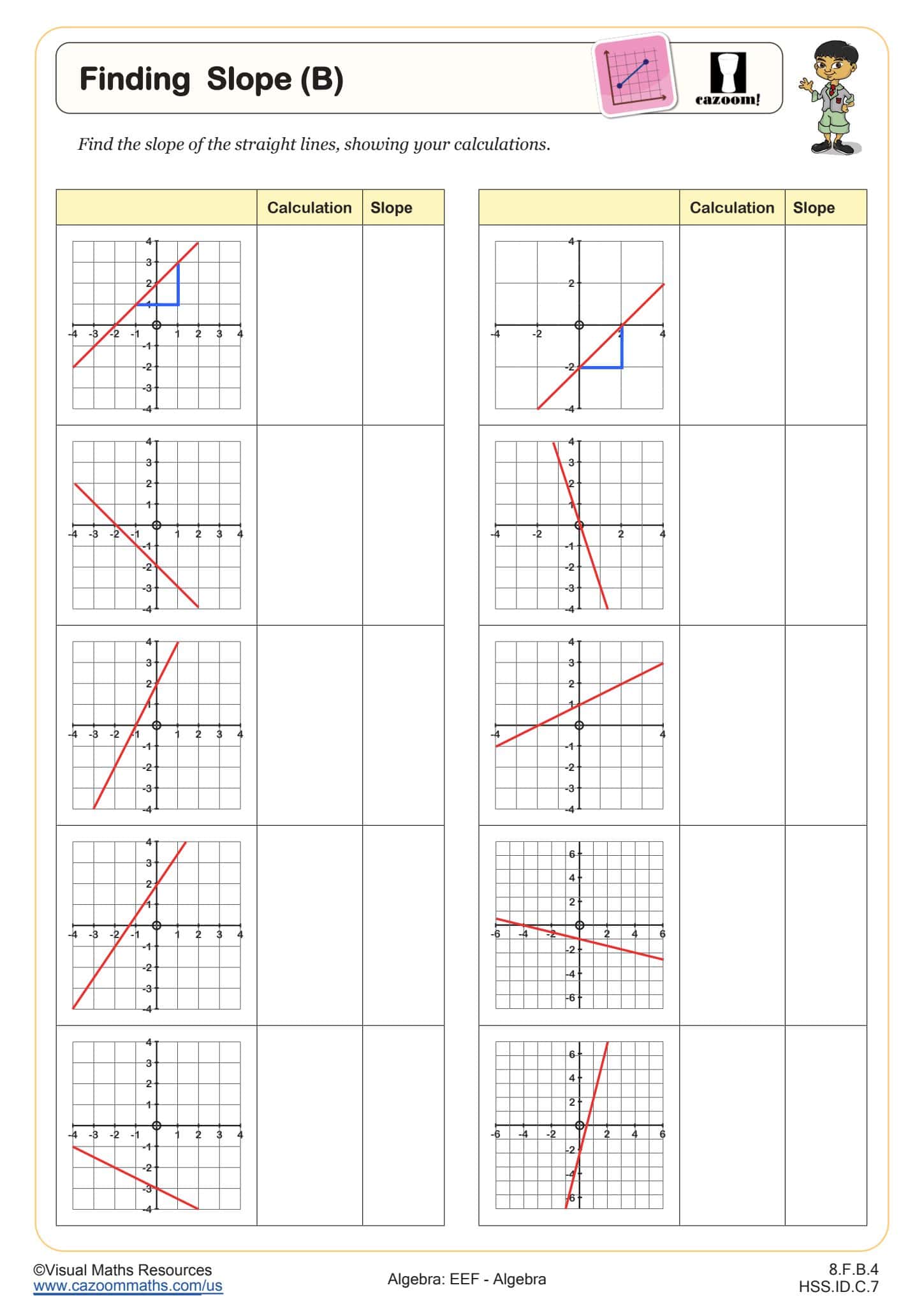
Finding Slope (C)
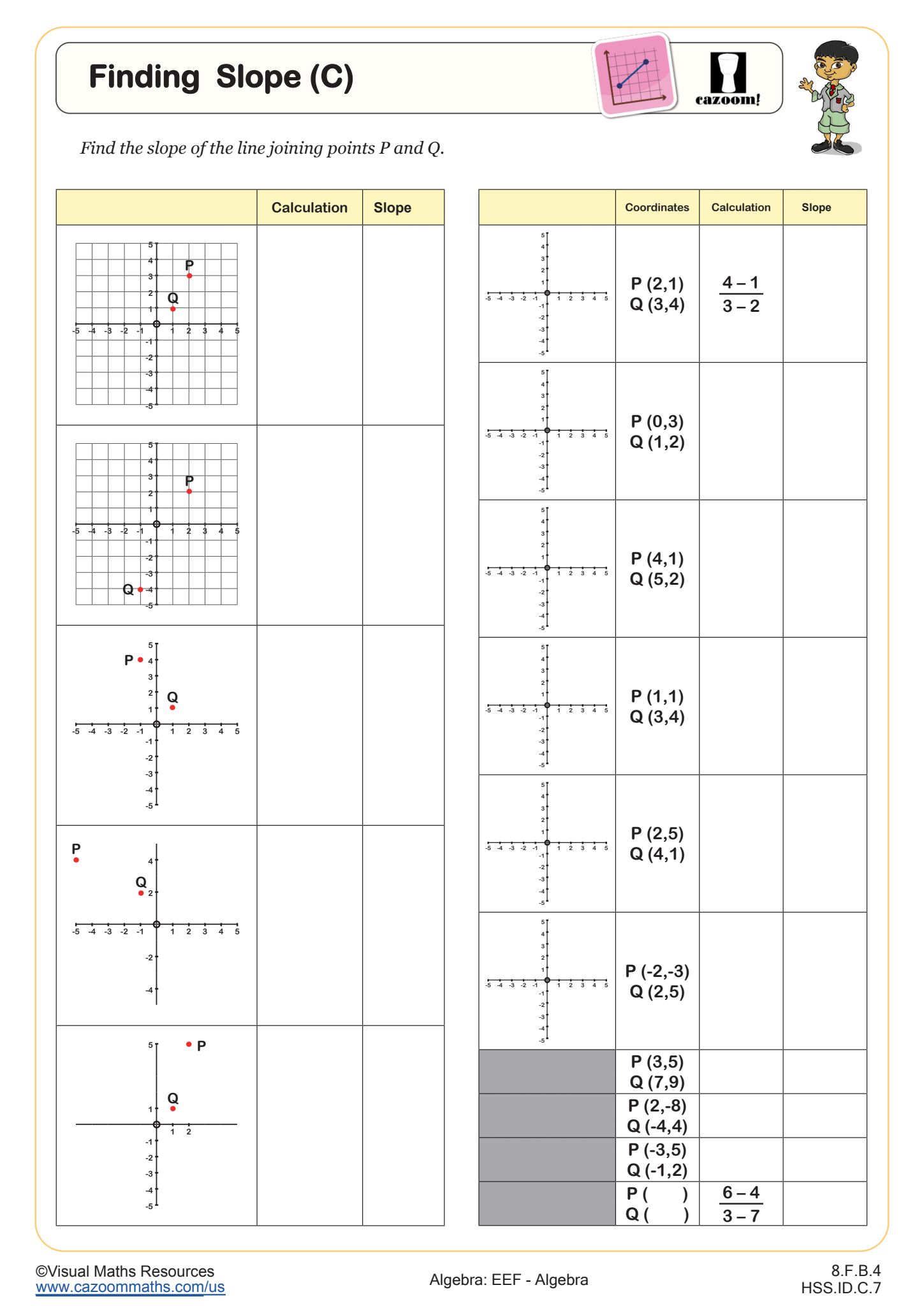
Form and Solve Linear Simultaneous Equations
Language of Algebra

Rationalizing the Denominator - First Steps

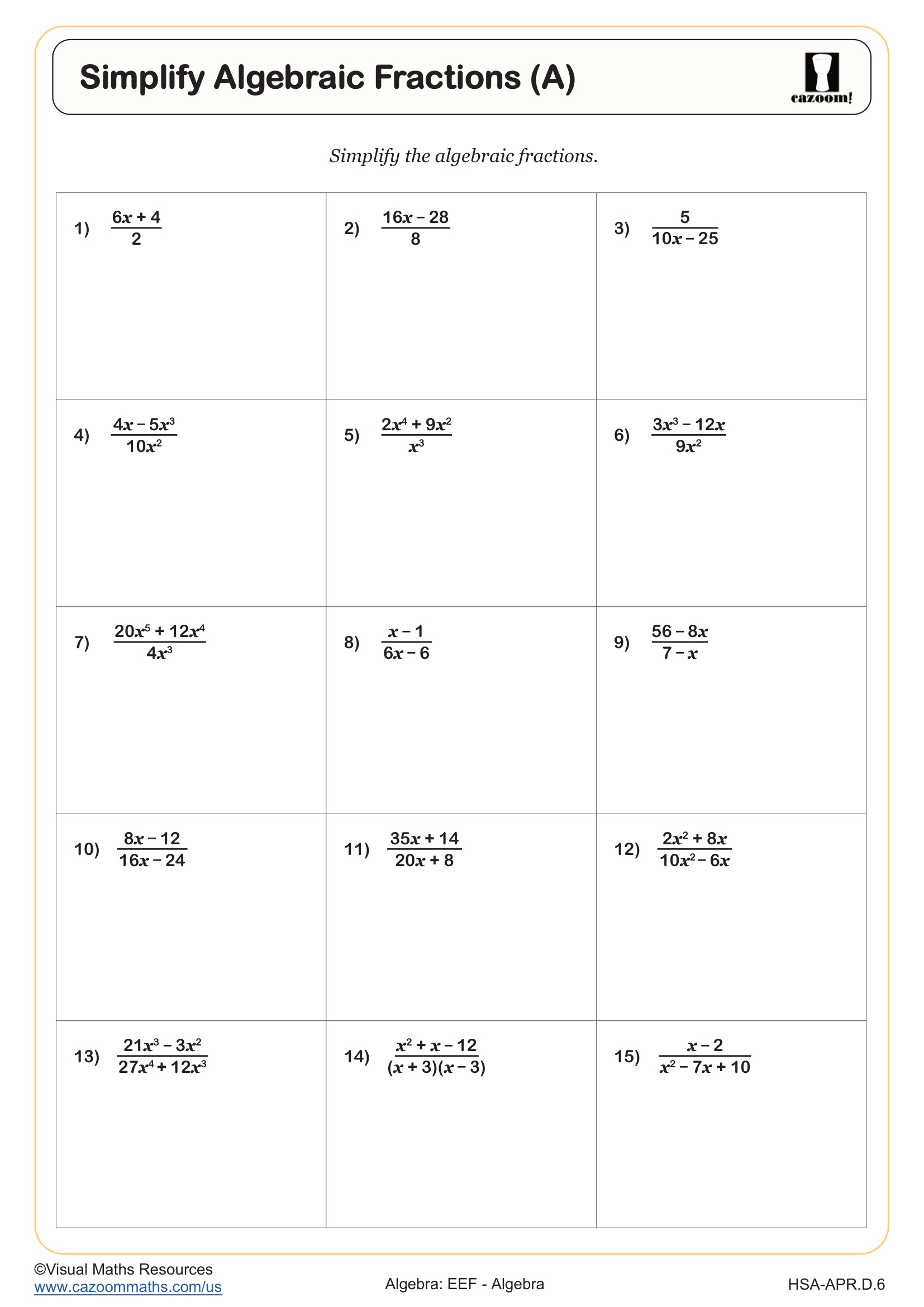
Simplify Algebraic Fractions (A)
Simplify Algebraic Fractions (B)

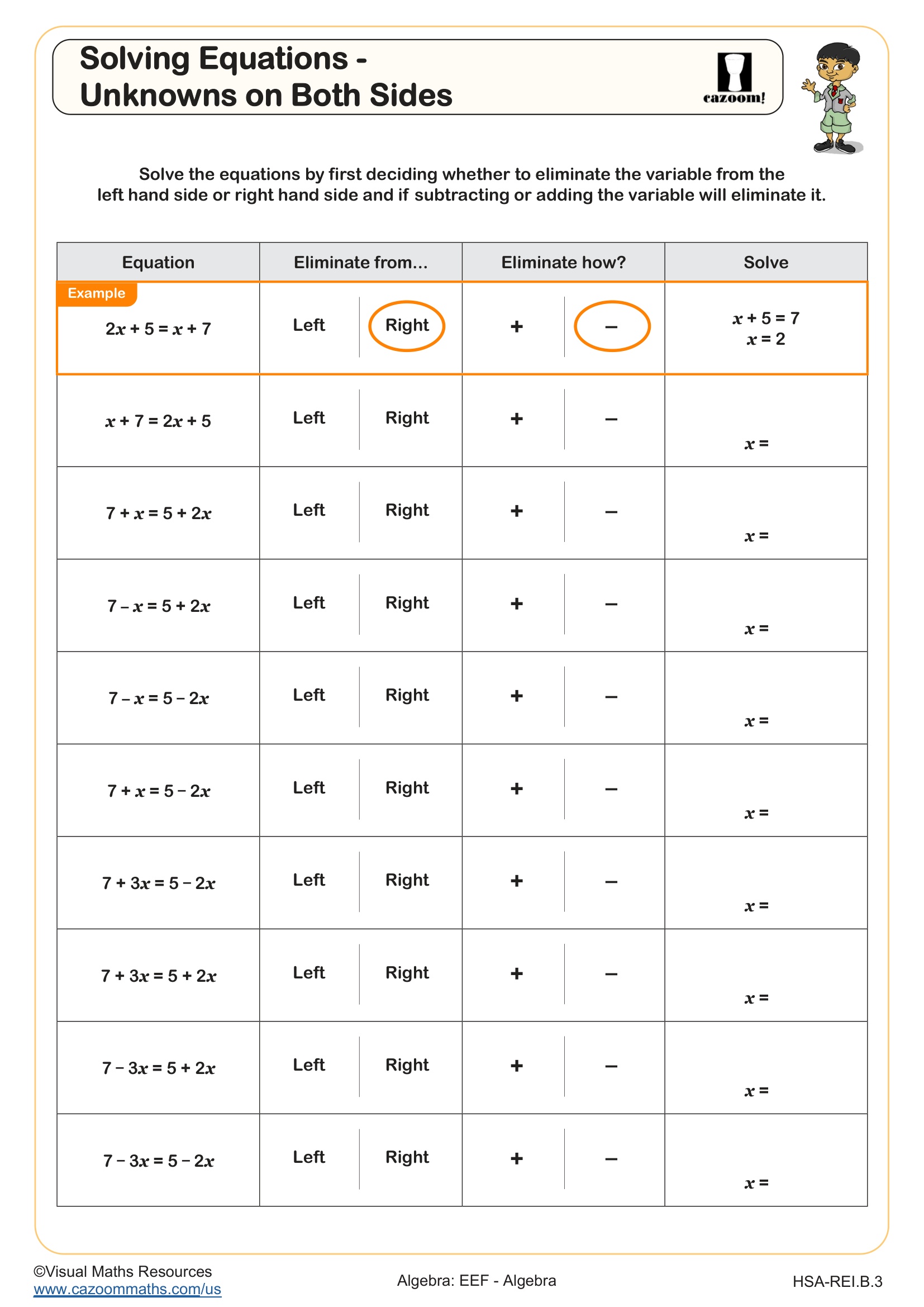
Solving Equations - Unknowns on Both Sides
Solving Linear Equations - 15 Minute Challenge (A)

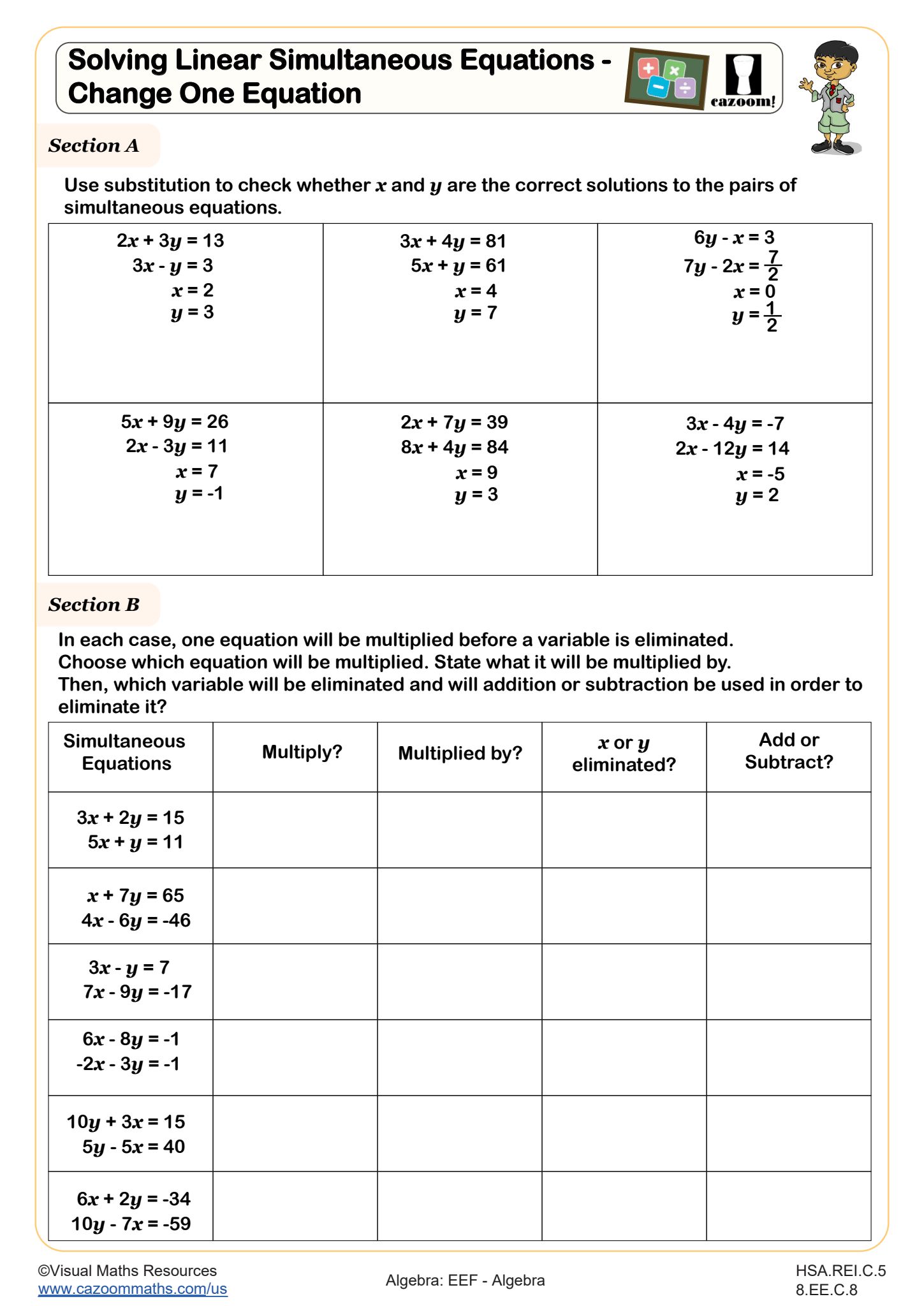
Solving Linear Simultaneous Equations - Change One Equation
What algebra concepts do students learn in Integrated Math 1?
Integrated Math 1 introduces students to core algebraic concepts including translating between verbal and symbolic representations, solving linear equations using properties of equality, understanding slope as a rate of change, and simplifying algebraic expressions and fractions. This course typically combines algebra with geometry and statistics, so students apply algebraic reasoning across multiple mathematical contexts rather than studying algebra in isolation.
Students frequently struggle when transitioning from arithmetic to algebraic thinking, particularly when variables represent unknown quantities rather than specific numbers. Teachers notice that students gain confidence once they recognize patterns in equation solving, such as always performing inverse operations in reverse order. Practice with varied problem types helps students develop flexibility in their approach rather than relying on memorized procedures.
How does Integrated Math 1 algebra appear on standardized tests?
Standardized assessments like the SAT, ACT, and state tests evaluate students' ability to create and solve linear equations from real-world scenarios, interpret slope in context, and manipulate algebraic expressions. Questions often require students to recognize equivalent forms of expressions or select equations that model given situations. Tests emphasize conceptual understanding alongside procedural fluency, asking students to explain why methods work rather than simply apply algorithms.
Students lose points when they fail to check their solutions in the original equation or misinterpret what a variable represents in context. Many students also struggle with multi-step problems that combine several skills, such as simplifying an expression before solving an equation. Teachers observe that students who practice translating word problems into algebraic notation perform better on standardized tests because they can identify mathematical relationships within complex scenarios.
Why is understanding slope important in Integrated Math 1?
Slope measures the rate of change between two variables and appears throughout Integrated Math 1 as students analyze linear relationships. Students calculate slope from graphs, tables, two points, and equations, learning that slope represents both steepness and direction. Teachers notice that students often confuse rise over run with run over rise, particularly when working with negative slopes or when points are presented in non-standard order.
Slope connects directly to real-world applications in fields like economics (cost per unit), physics (velocity as change in distance over time), and engineering (grade of a road or ramp). Students encounter slope again in later courses when studying derivatives in calculus, making it a foundational concept for STEM pathways. College-bound students benefit from recognizing slope in various representations since standardized tests and college placement exams frequently test this concept across multiple contexts.
How can teachers use these algebra worksheets in Integrated Math 1 classrooms?
These worksheets provide structured practice that builds from foundational concepts to more challenging applications. The variety of formats, including timed challenges, pyramids, and fraction simplification, keeps students engaged while reinforcing essential skills. Teachers can use scaffolded worksheets to differentiate instruction, assigning different difficulty levels based on student readiness. The complete answer keys allow students to check their work independently, promoting self-assessment and error analysis.
Many teachers use these worksheets for test preparation, assigning them as homework before unit assessments or state testing windows. The 15-minute challenge format works well as warm-up activities or exit tickets to gauge student understanding quickly. Worksheets also serve effectively in intervention settings where students need targeted practice on specific skills. Paired work with these materials encourages mathematical discourse as students explain their reasoning and identify mistakes together.