Integrated Math 1 Area and Perimeter Worksheets
What area and perimeter skills do Integrated Math 1 students practice?
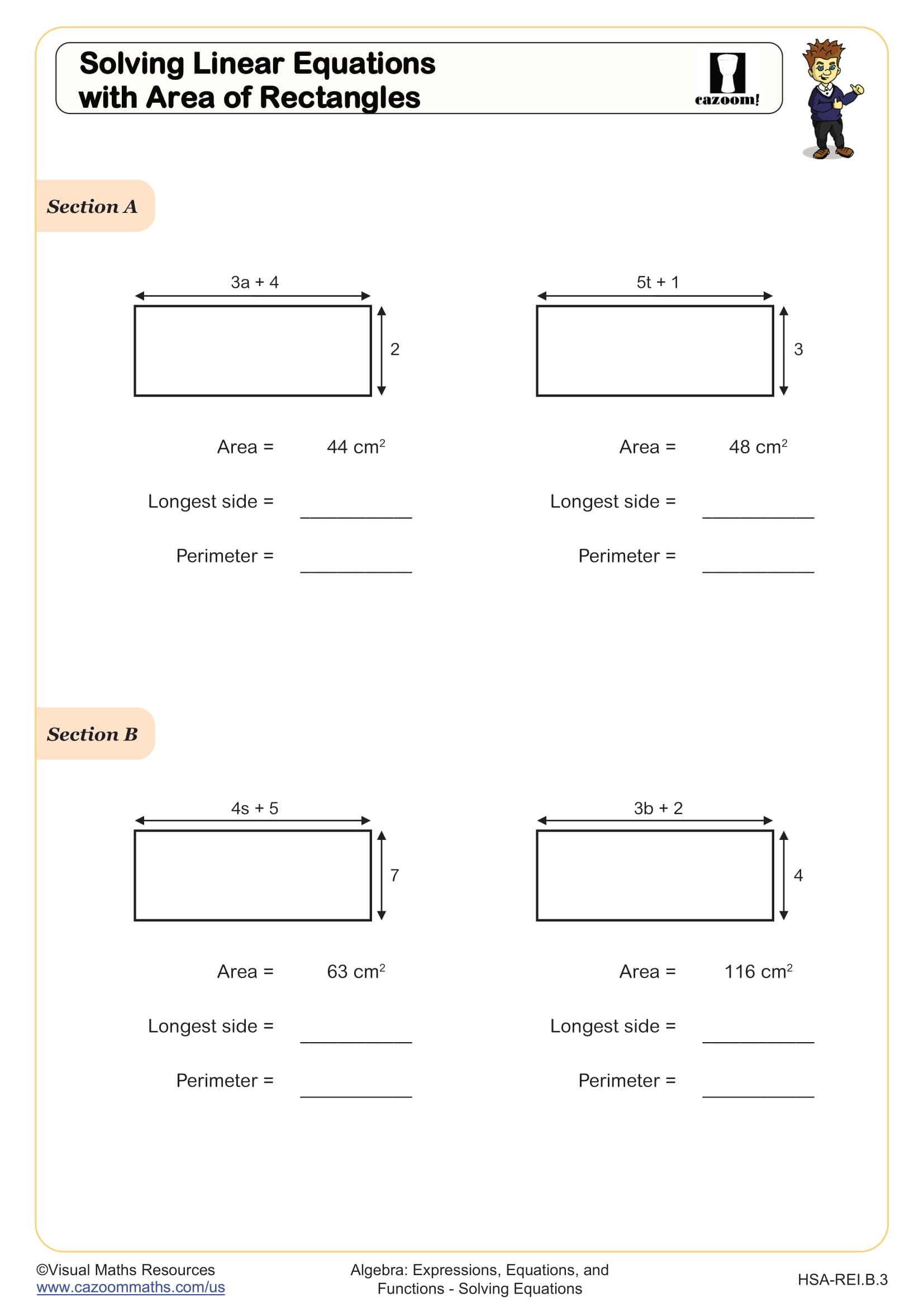
Integrated Math 1 students move beyond calculating basic area and perimeter with numeric values to working with algebraic expressions representing dimensions. Students apply the formulas A = lw and P = 2l + 2w while solving for unknown variables, which aligns with Common Core standards that emphasize modeling with mathematics and reasoning with equations. This integration of geometry and algebra prepares students for more complex problem-solving in later courses.
A common error occurs when students see an expression like (x + 3) for length and correctly write 2(x + 3) for part of the perimeter formula, but then fail to distribute the 2 before combining like terms. Teachers find that having students write out each step separately, rather than attempting mental math, significantly reduces this mistake and builds confidence with the distributive property in context.
How do standardized tests assess area and perimeter concepts?
The SAT and ACT regularly include problems where students must determine missing dimensions given area or perimeter information, often within word problem contexts. State assessments aligned with Common Core standards expect students to formulate equations from geometric constraints and solve them accurately. Test questions frequently combine multiple steps, requiring students to first write an equation representing the situation, then solve it, and finally interpret the solution in the original context.
Students lose points when they solve for a variable but fail to answer the actual question being asked. For example, if a problem asks for the perimeter but students only find x and stop, they miss the final calculation. Another frequent mistake occurs when students forget to check whether their solution makes sense geometrically, accepting negative lengths or widths that would be impossible in real rectangles.
Why is setting up equations from geometric constraints important?
Setting up equations from area and perimeter constraints teaches students to translate between visual representations and algebraic models, a foundational skill for mathematical modeling. Students learn to identify what they know, what they need to find, and how geometric formulas create the bridge between the two. This process strengthens their ability to move fluidly between different representations of the same problem, which appears throughout higher mathematics and standardized testing.
This skill has direct applications in construction, landscaping, and design fields where professionals must calculate dimensions based on space or material constraints. Architects determining room dimensions given floor area requirements or landscapers calculating fence length for a specified yard area use exactly this type of reasoning. College-bound students encounter similar problems in calculus optimization and physics problems involving rectangular regions, making early mastery particularly valuable.
How can teachers effectively use these area and perimeter worksheets?
These worksheets provide structured practice that allows students to develop fluency with the multi-step process of extracting information from geometric diagrams, writing appropriate equations, and solving them algebraically. The problems progressively build complexity, helping students recognize patterns in how geometric constraints translate into algebraic equations. Having complete answer keys enables teachers to quickly identify where students make errors in their solution process, whether in setting up the initial equation or in the algebraic manipulation.
Many teachers use these worksheets as bellwork to activate prior knowledge before introducing new equation-solving techniques, or as targeted practice when reviewing for unit tests and semester exams. The problems work well for paired activities where students can discuss their reasoning about which formula to apply and how to set up the equation. Teachers also find them valuable for differentiated instruction, providing additional support for students who need more practice connecting geometry and algebra before moving to more abstract equation-solving contexts.