Integrated Math 1 Circles Worksheets
What Circle Concepts Do Students Learn in Integrated Math 1?
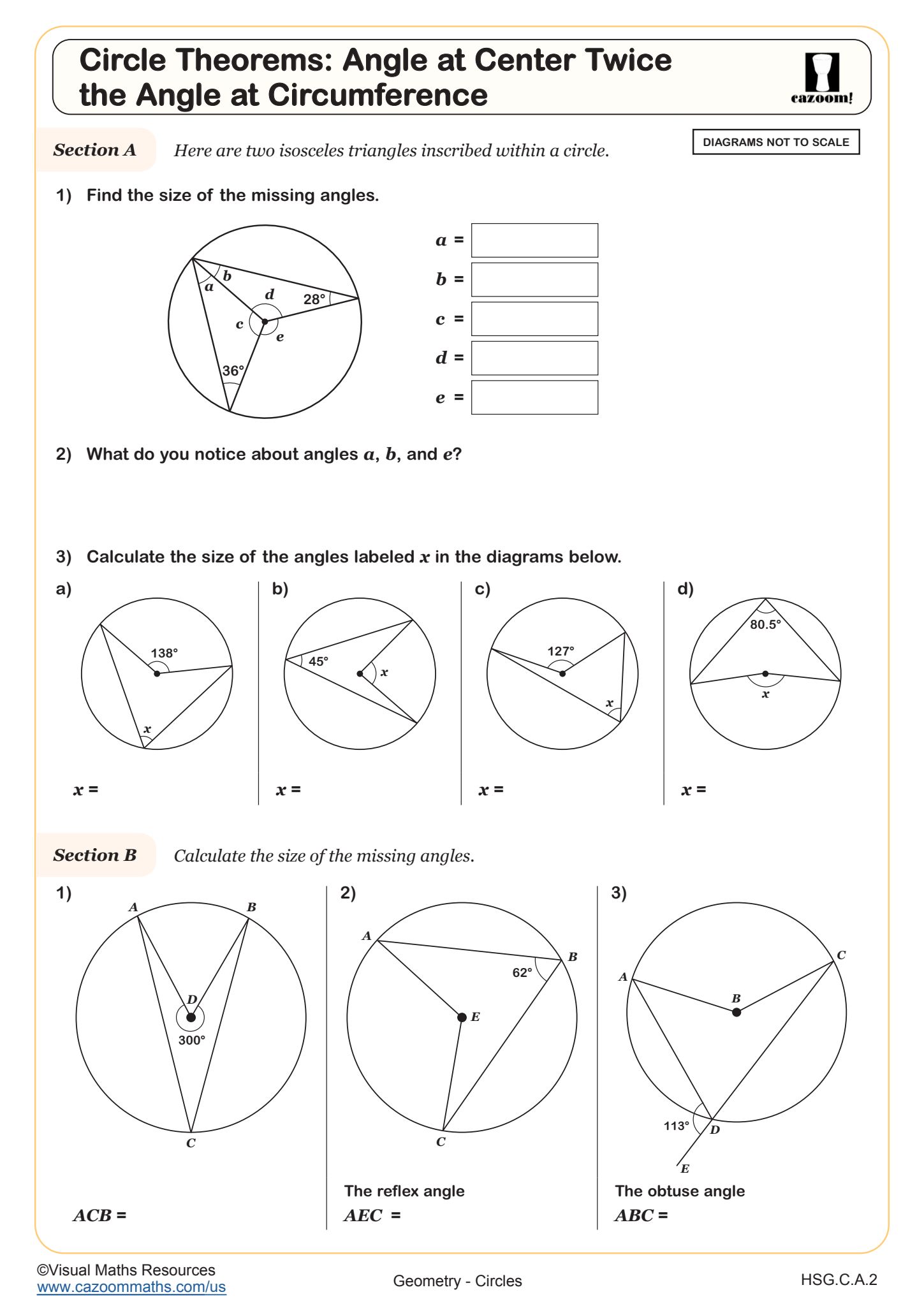
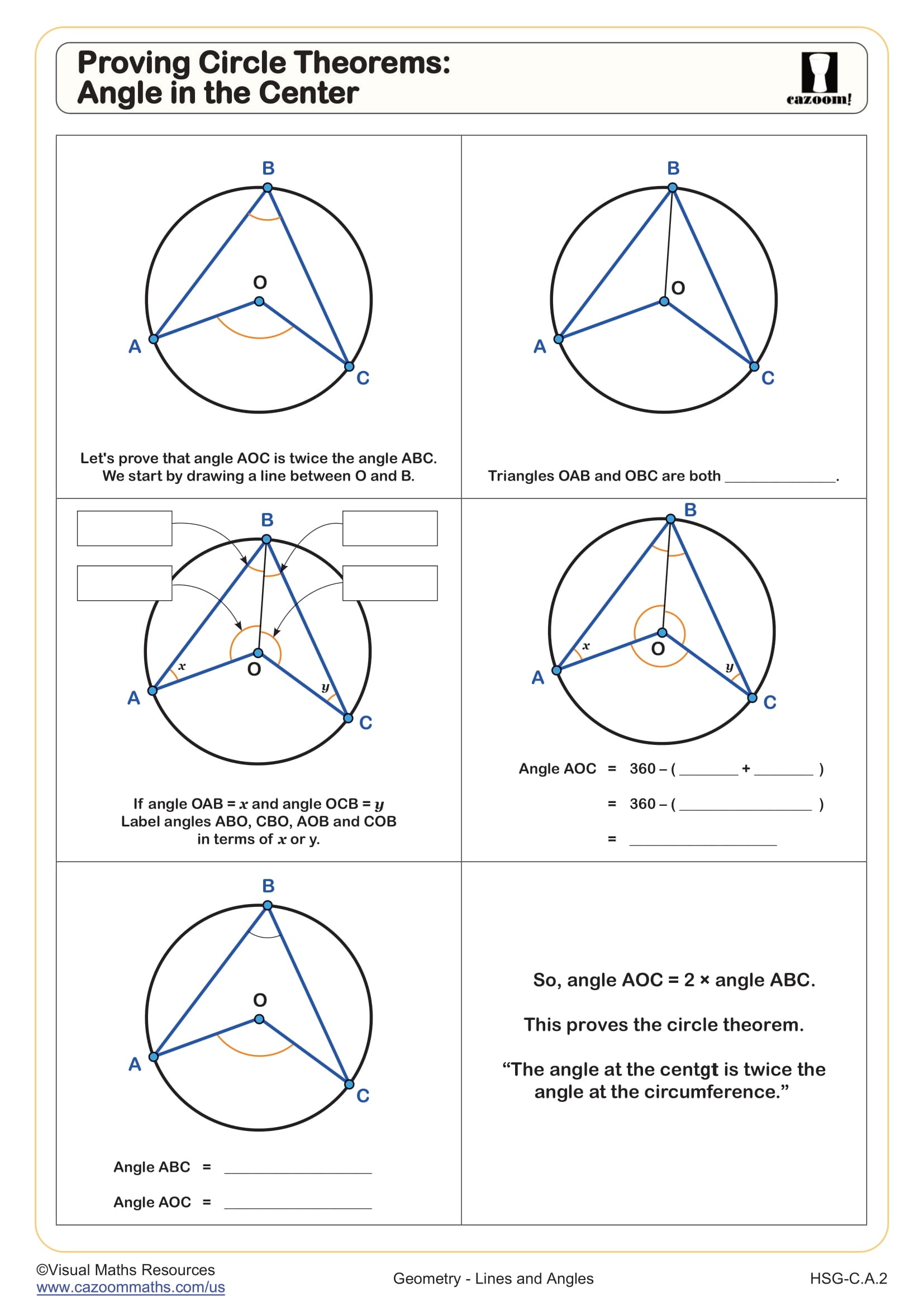
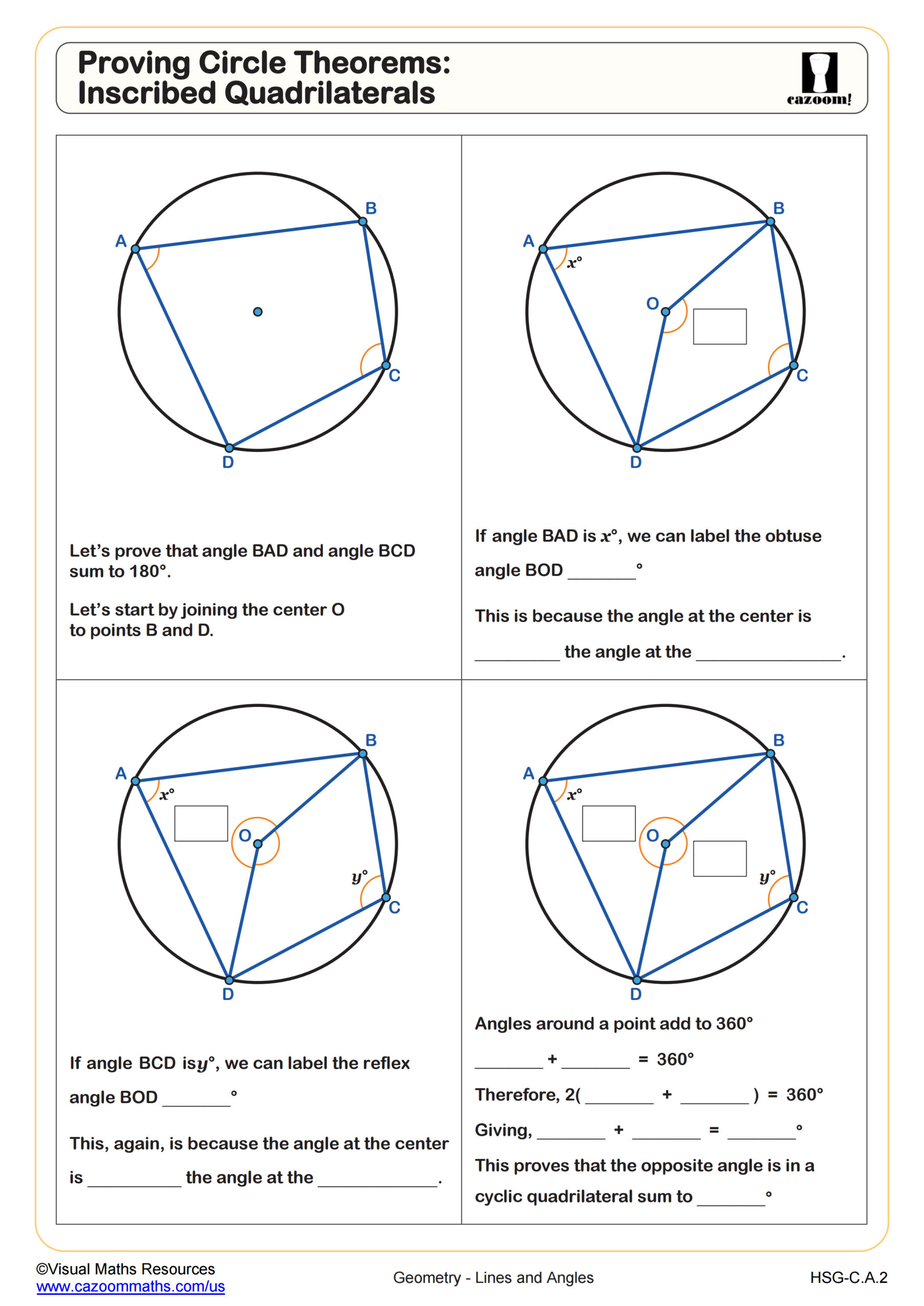
Integrated Math 1 introduces students to fundamental circle theorems that connect algebra and geometry. Students explore the relationship between central angles and inscribed angles, work with inscribed quadrilaterals and their opposite angle properties, and learn that an angle at the center is twice the angle at the circumference when both intercept the same arc. These concepts align with Common Core standards for geometric reasoning and proof.
Students frequently confuse which angle is which when diagrams show multiple angles in the same circle. Teachers find that color-coding central angles differently from inscribed angles helps students categorize problems correctly before applying theorems. The inscribed quadrilateral theorem (opposite angles sum to 180 degrees) often surprises students because it works for any quadrilateral inscribed in a circle, not just special quadrilaterals they've studied before.
How Do Circle Theorems Appear on the SAT and State Assessments?
Standardized tests present circle theorem questions within multi-step geometry problems that require students to identify angle relationships and set up equations. The SAT Math section expects students to recognize when an inscribed angle intercepts a diameter (creating a right angle) and to apply the central angle theorem without being told which theorem to use. State assessments often embed circle problems within coordinate geometry or ask students to explain their reasoning using geometric properties.
Students lose points when they memorize theorems without understanding the visual conditions that trigger each one. A common error involves assuming all angles in a circle follow the same rules, leading students to incorrectly double inscribed angles or halve angles that aren't central. Test-takers who sketch and label angle types before calculating typically avoid these mistakes and complete circle problems more accurately under time pressure.
What Makes Inscribed Angle Theorem Essential for Geometry?
The inscribed angle theorem states that an angle inscribed in a circle measures half the central angle that intercepts the same arc. This relationship gives students a reliable method for finding unknown angle measures when circles contain multiple inscribed or central angles. The theorem extends to the special case where an inscribed angle intercepts a semicircle, creating a 90-degree angle that students use frequently in proof problems and construction tasks.
Architects and engineers apply inscribed angle properties when designing circular structures like amphitheaters, where sightlines from different seating positions need to maintain specific viewing angles. The Thales' theorem application (semicircle creating a right angle) appears in satellite dish design and radio telescope engineering, where signals reflecting off parabolic surfaces must meet at precise angles. Students headed toward STEM fields encounter these circle properties again in trigonometry, physics optics, and calculus when studying circular motion.
How Do These Worksheets Support Integrated Math 1 Circle Learning?
The worksheets progress from guided proof problems that walk students through circle theorem applications to construction activities that build spatial visualization skills. Each worksheet includes diagrams with varying complexity, helping students recognize circle theorems across different visual presentations. The proof-based exercises develop logical reasoning while construction tasks like the Easter egg dimension problems connect geometric concepts to design thinking and measurement precision.
Teachers use these worksheets for differentiated practice, assigning proof problems to students ready for challenge while directing others toward construction activities that build conceptual understanding through hands-on work. The answer keys make them effective for test review stations where students check their work independently, or for homework assignments that prepare students for upcoming circle theorem assessments. Paired work on construction problems encourages students to verbalize their geometric reasoning, strengthening both understanding and mathematical communication skills.