Integrated Math 1 Indices Worksheets
What Do Students Learn About Indices in Integrated Math 1?
In Integrated Math 1, indices (also called exponents) cover the laws of exponents including multiplication and division of like bases, power of a power, zero and negative exponents, and the relationship between radicals and fractional exponents. Students work with expressions like x⁻³, (2³)², and converting √x to x^(1/2). This topic aligns with Common Core standards that emphasize understanding structure in algebraic expressions.
A common misconception emerges when students encounter negative exponents—many initially believe x⁻² equals -x² rather than 1/x². Teachers observe that students who practice converting negative exponents to fractions first, then simplifying, develop stronger conceptual understanding than those who simply apply a memorized rule. The worksheets progress from basic exponent rules through more complex combinations involving multiple properties.
How Are Indices Tested on the SAT and State Assessments?
Standardized tests embed exponent rules within algebraic manipulation problems rather than testing them in isolation. Students encounter expressions requiring simplification before solving equations, or must recognize equivalent forms like whether 2⁻³ equals 1/8. The SAT calculator section expects fluency with negative and fractional exponents when working with exponential functions and growth models.
Students lose points when they incorrectly distribute exponents across addition, writing (x + y)² as x² + y² instead of recognizing it requires expansion. Another frequent error involves sign mistakes with negative bases raised to powers—confusing (-3)² with -3². Teachers notice that students who regularly practice mixed exponent problems perform significantly better on assessment questions that combine multiple properties in one expression.
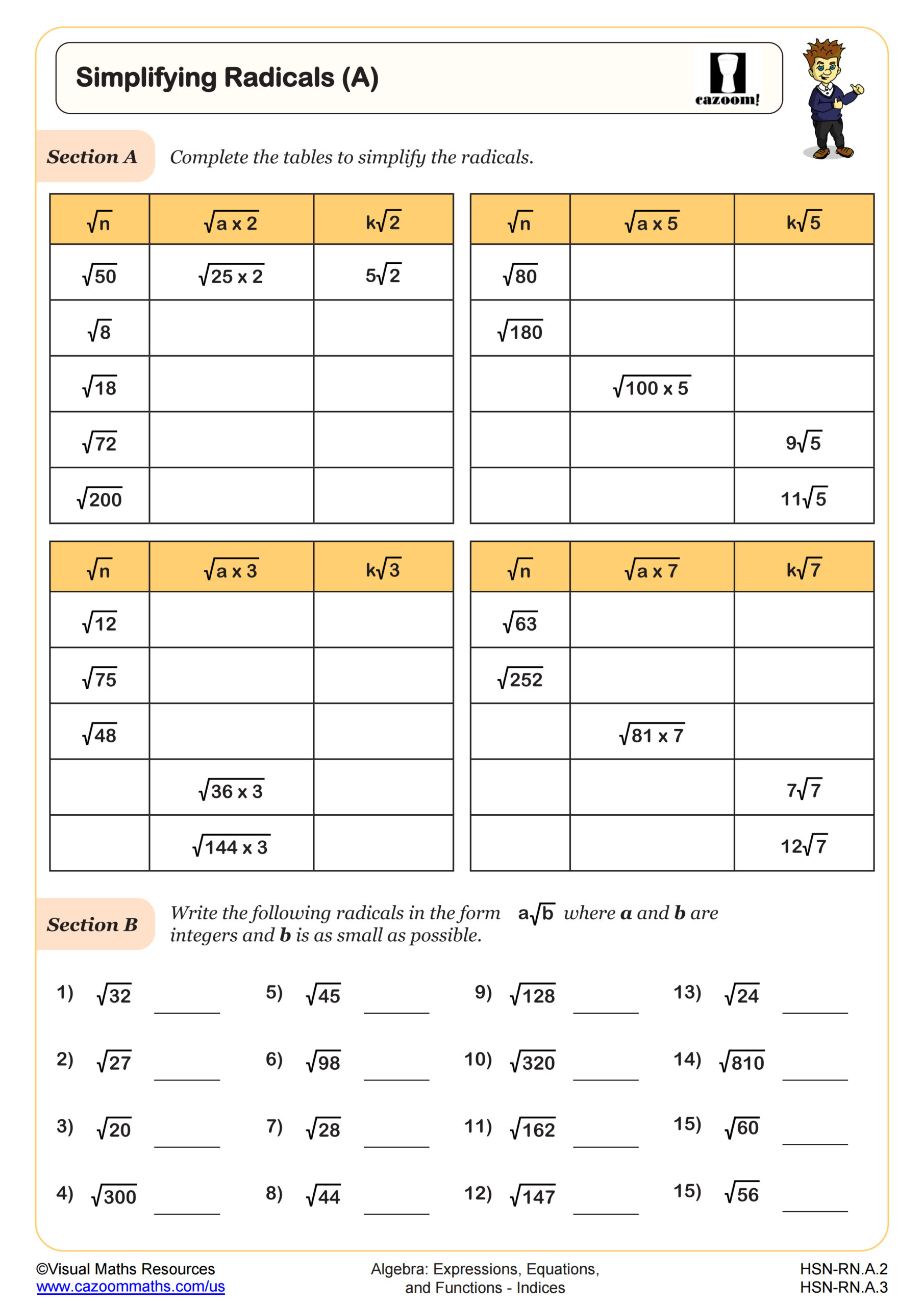
Why Is Simplifying Radicals Important for Integrated Math 1?
Simplifying radicals teaches students to recognize perfect square factors and rewrite expressions in simplest form—skills that become necessary when solving quadratic equations and working with irrational numbers. Students learn to break down √72 into √36 × √2, simplifying to 6√2. Understanding that √x² = |x| prevents errors when solving equations, and connecting √x to x^(1/2) bridges radical notation to exponent rules students already know.
This skill appears throughout STEM fields where measurements involve roots and powers. Engineers use radical simplification when calculating distances in three-dimensional space, and physicists apply these concepts when working with inverse square laws in electromagnetism and gravity. College-bound students encounter radicals regularly in calculus when finding derivatives of root functions, making this foundational practice valuable beyond Integrated Math 1.
How Should Teachers Use These Indices Worksheets in Integrated Math 1?
The worksheets provide scaffolded practice starting with single-property applications before combining multiple exponent rules. Teachers can assign specific worksheets targeting the exact concept students found challenging on recent assessments—whether that's negative exponents, radical simplification, or changing bases. The answer keys allow students to self-check during independent practice, helping them identify which steps in their work contain errors.
Many teachers use these worksheets for spiral review by assigning one as a warm-up weeks after initially teaching indices, ensuring retention before polynomial multiplication. The resources work well for differentiated instruction—students needing reinforcement can work through the foundational worksheets while advanced students tackle problems requiring multiple conversions between radical and exponential form. Paired practice helps struggling students verbalize their thinking when a peer explains why 5⁻² becomes 1/25.