Integrated Math 1 Inequalities Worksheets
What Do Students Learn About Inequalities in Integrated Math 1?
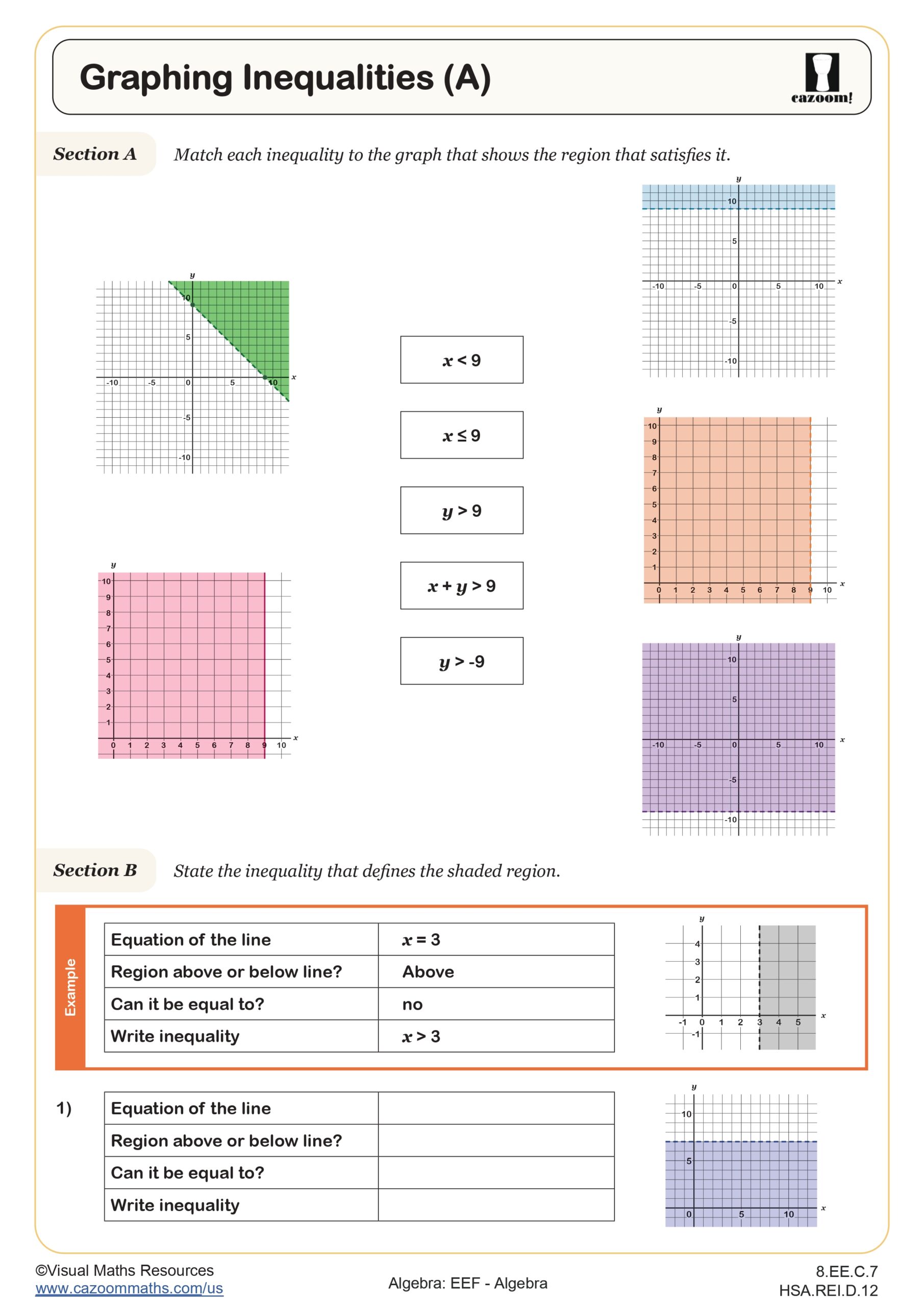
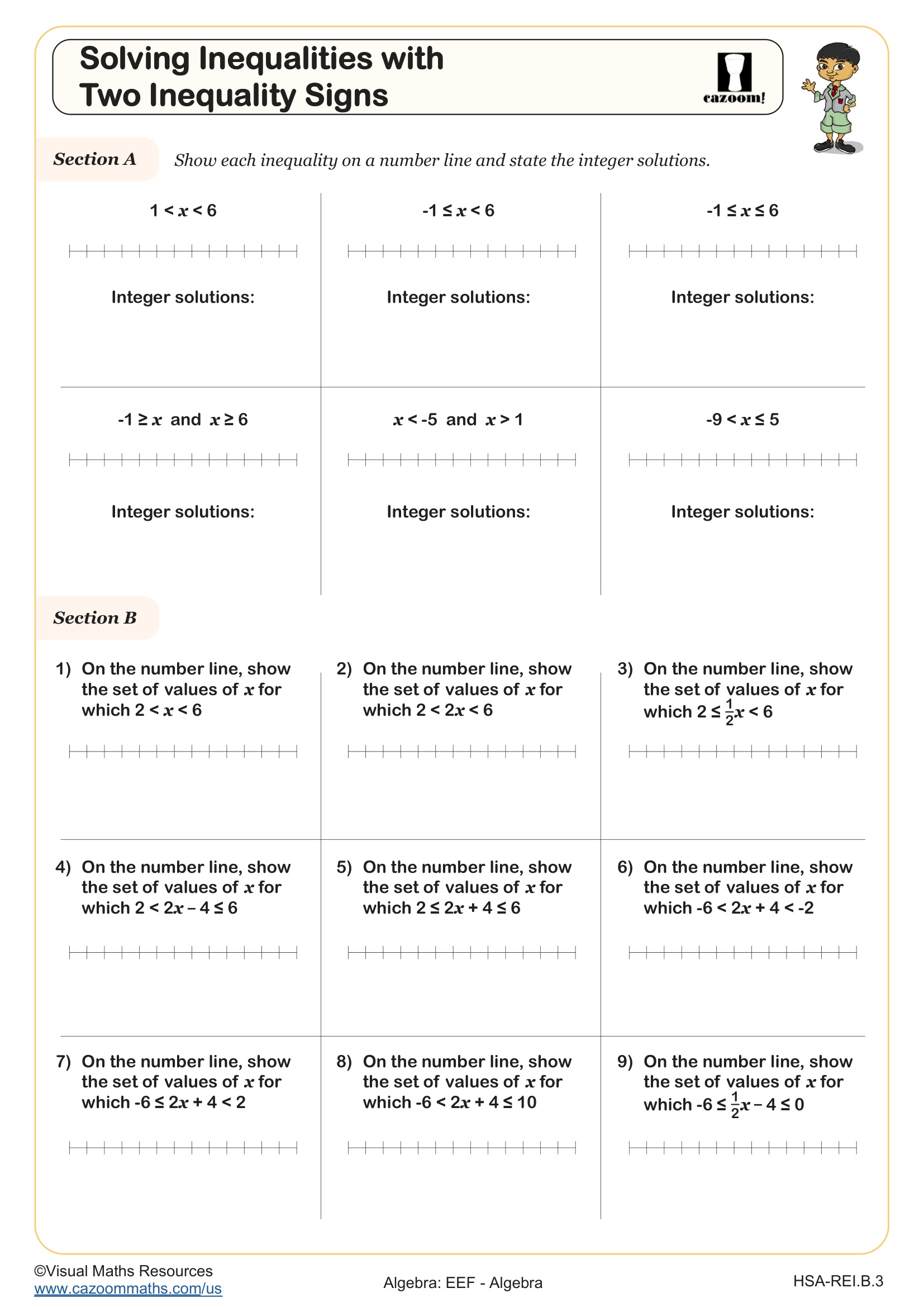
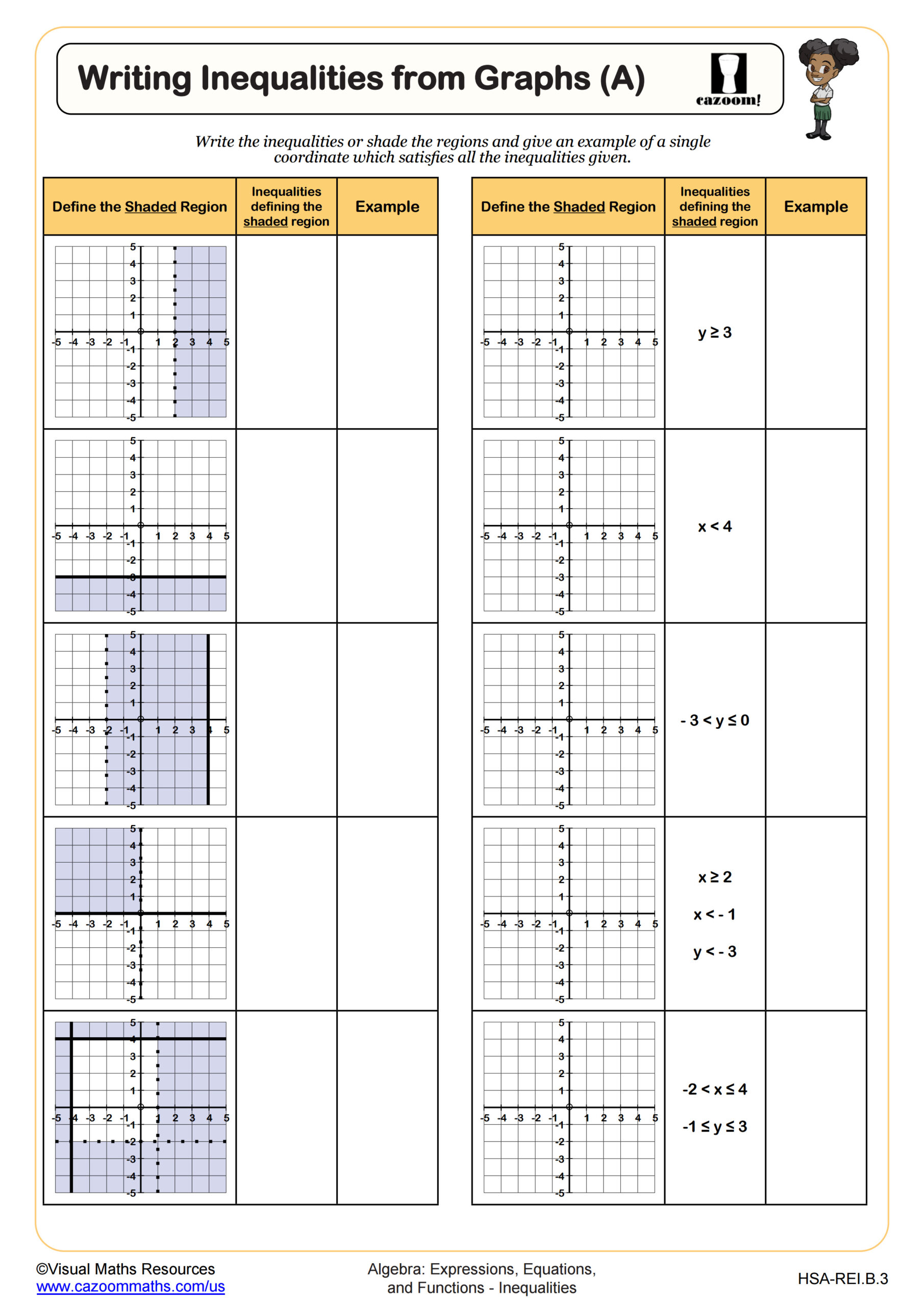
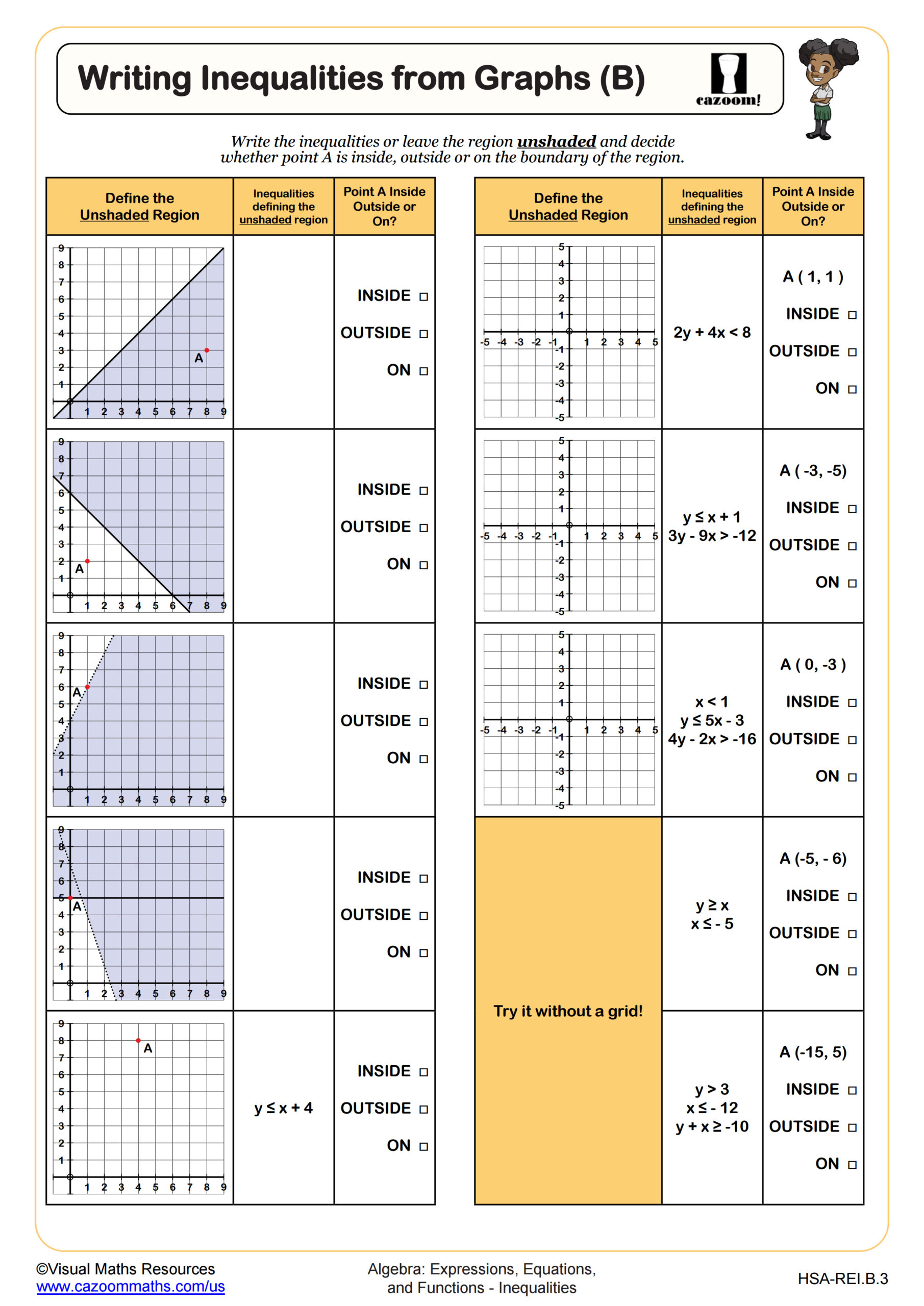
In Integrated Math 1, students develop fluency with writing, solving, and graphing one-variable inequalities, including compound inequalities that involve two inequality signs. The curriculum aligns with Common Core standards that require students to represent and solve problems using inequalities, interpret solution sets graphically, and understand the difference between discrete and continuous solutions. Students work with inequalities in standard form, practice translating word problems into inequality notation, and learn to represent solutions on number lines using open and closed circles.
Many students initially treat inequality symbols as interchangeable, writing x > 5 when they mean x < 5 after dividing by a negative coefficient. Teachers often observe that students grasp the concept more quickly when they substitute test values from their solution set back into the original inequality to verify their answer makes logical sense. This verification step reinforces why the direction of the inequality symbol matters and builds confidence in their algebraic manipulations.
How Are Inequalities Tested on the SAT and State Assessments?
Standardized tests like the SAT and ACT present inequalities in multiple contexts, including algebraic expressions, word problems requiring translation into inequality notation, and questions asking students to interpret solution sets from graphs. Students must demonstrate understanding of compound inequalities, often written in the form a < x < b, and recognize which values satisfy given conditions. State assessments aligned with Common Core frequently include real-world scenarios where students must write and solve inequalities to model constraints or limitations.
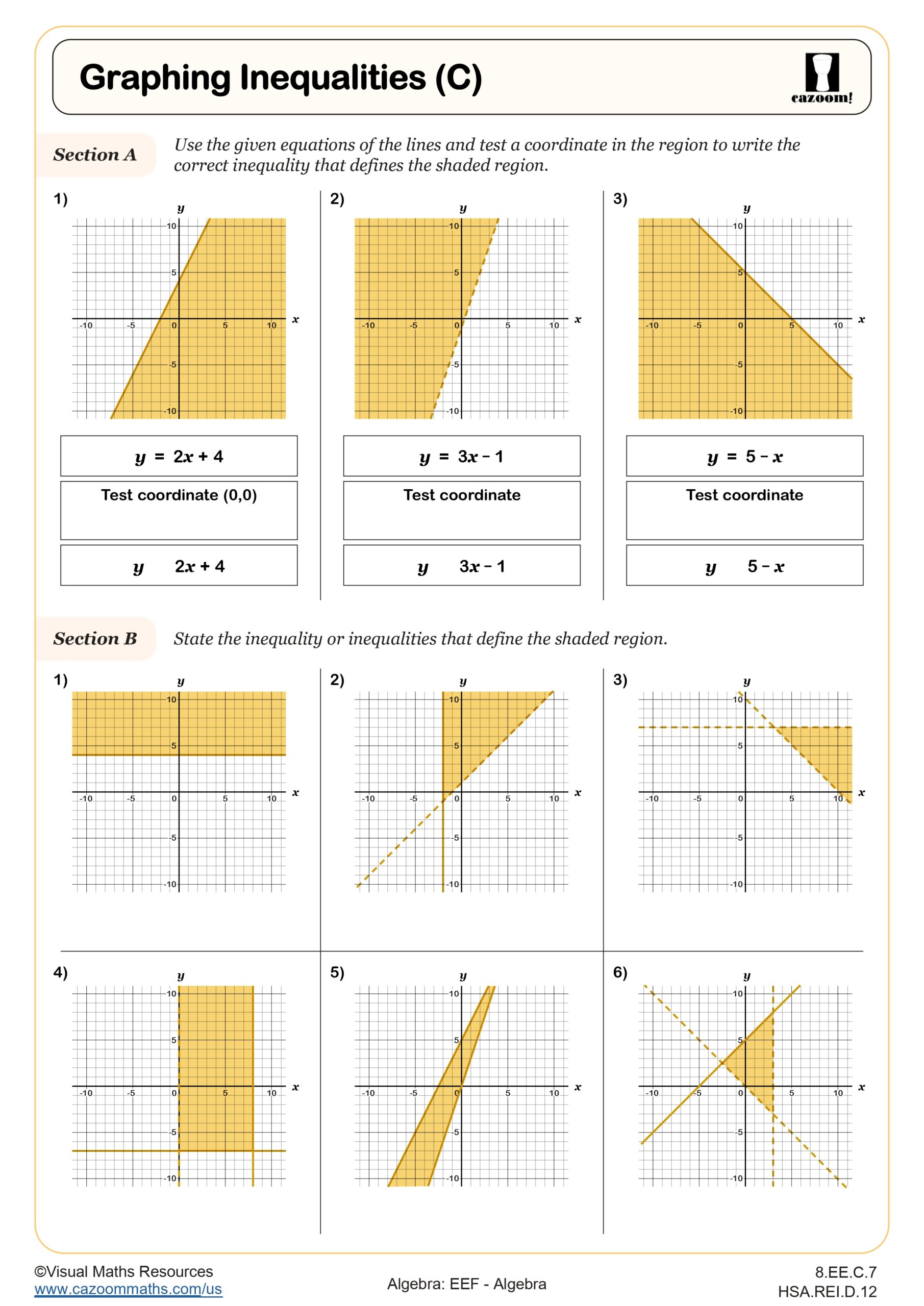
Students lose points when they forget to reverse the inequality symbol after multiplying or dividing by negative values, a mistake that appears consistently across all standardized testing formats. Another common error occurs when students misinterpret whether boundary points should be included in the solution set, particularly when converting between graph and symbolic representations. Tests also assess whether students can identify which inequality matches a given graph, requiring attention to open versus closed circles and the direction of shading or arrows.
What Are Compound Inequalities and Why Do They Matter?
Compound inequalities combine two inequality statements into one expression, either as a conjunction (AND, written as a < x < b) or a disjunction (OR, written as x < a or x > b). Students learn to solve each part separately while maintaining the relationship between the variable and boundary values. For conjunction inequalities, the solution set represents the overlap where both conditions are true simultaneously, while disjunction inequalities create two separate solution regions. Teachers notice that students often confuse which type they're working with, especially when translating verbal descriptions into mathematical notation.
Compound inequalities appear throughout STEM fields when defining acceptable ranges for measurements, tolerances in manufacturing, or safe operating parameters. Engineers use compound inequalities to specify temperature ranges for materials, while quality control systems rely on them to flag products outside acceptable dimensions. In chemistry, compound inequalities define pH ranges for solutions, and in physics, they establish boundaries for variables in motion problems. College-bound students encounter compound inequalities again in precalculus when working with absolute value inequalities and in statistics when establishing confidence intervals.
How Can Teachers Use These Inequalities Worksheets in Integrated Math 1?
These worksheets provide scaffolded practice that progresses from graphing simple inequalities to interpreting complex solution sets from multiple representations. The collection includes varied problem types that address different aspects of the standard, allowing teachers to assign targeted practice based on individual student needs. Answer keys enable students to check their work independently during practice sessions, promoting self-assessment skills that prove valuable during test preparation. The worksheets also support differentiation, as students who master basic inequality concepts can advance to compound inequalities while others continue building foundational skills.
Many teachers use these worksheets for warm-up activities that reinforce previous lessons, as exit tickets to assess daily understanding, or as homework assignments that bridge classroom instruction with independent practice. The materials work particularly well for intervention groups who need additional repetition with reversing inequality symbols or for paired work where students compare their graphical representations and discuss discrepancies. Teachers preparing students for state assessments often incorporate these worksheets into review stations, allowing students to rotate through different inequality concepts while building stamina for longer problem sets typical of standardized tests.