Integrated Math 1 Polygons Worksheets
What Do Students Learn About Polygons in Integrated Math 1?
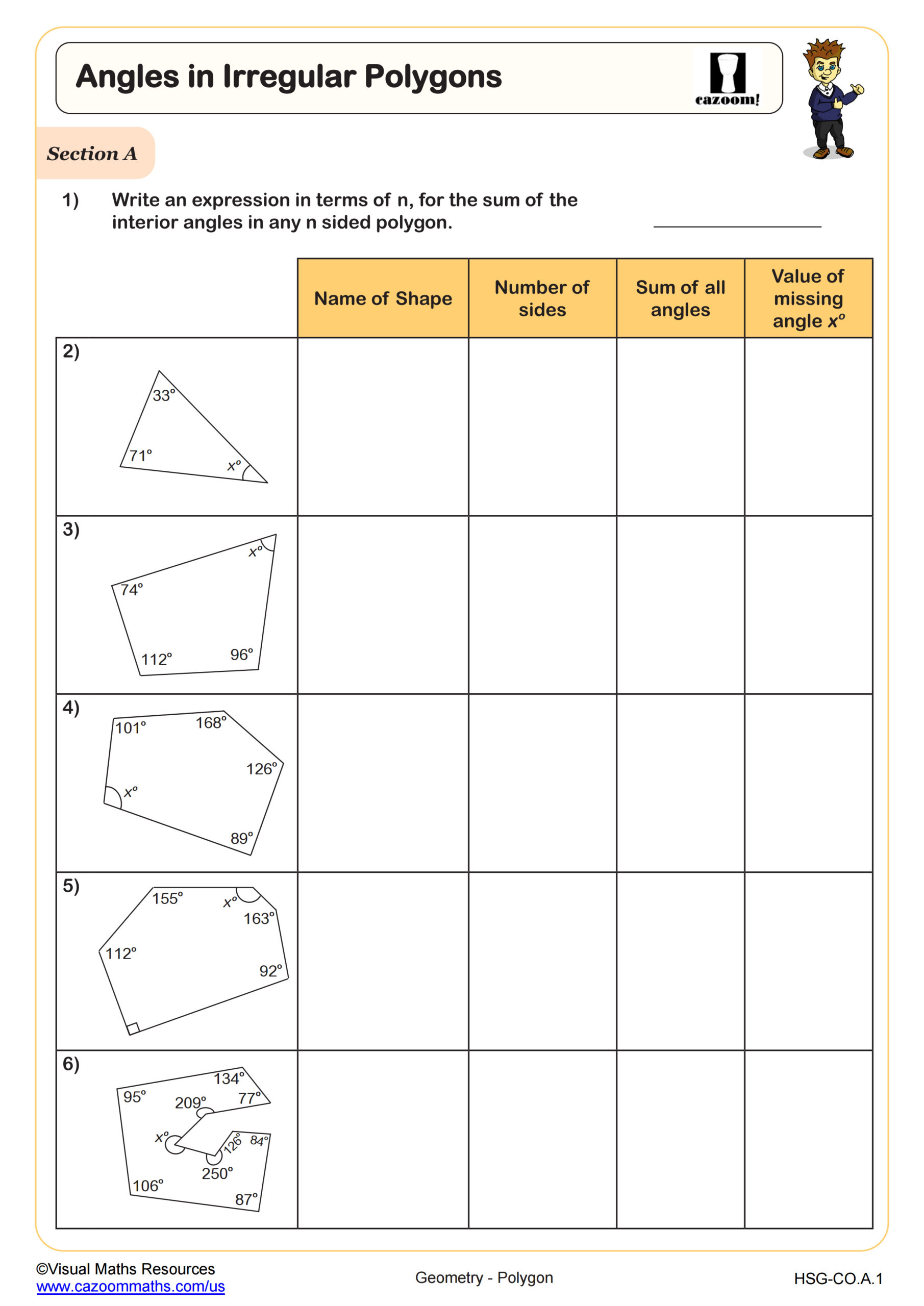
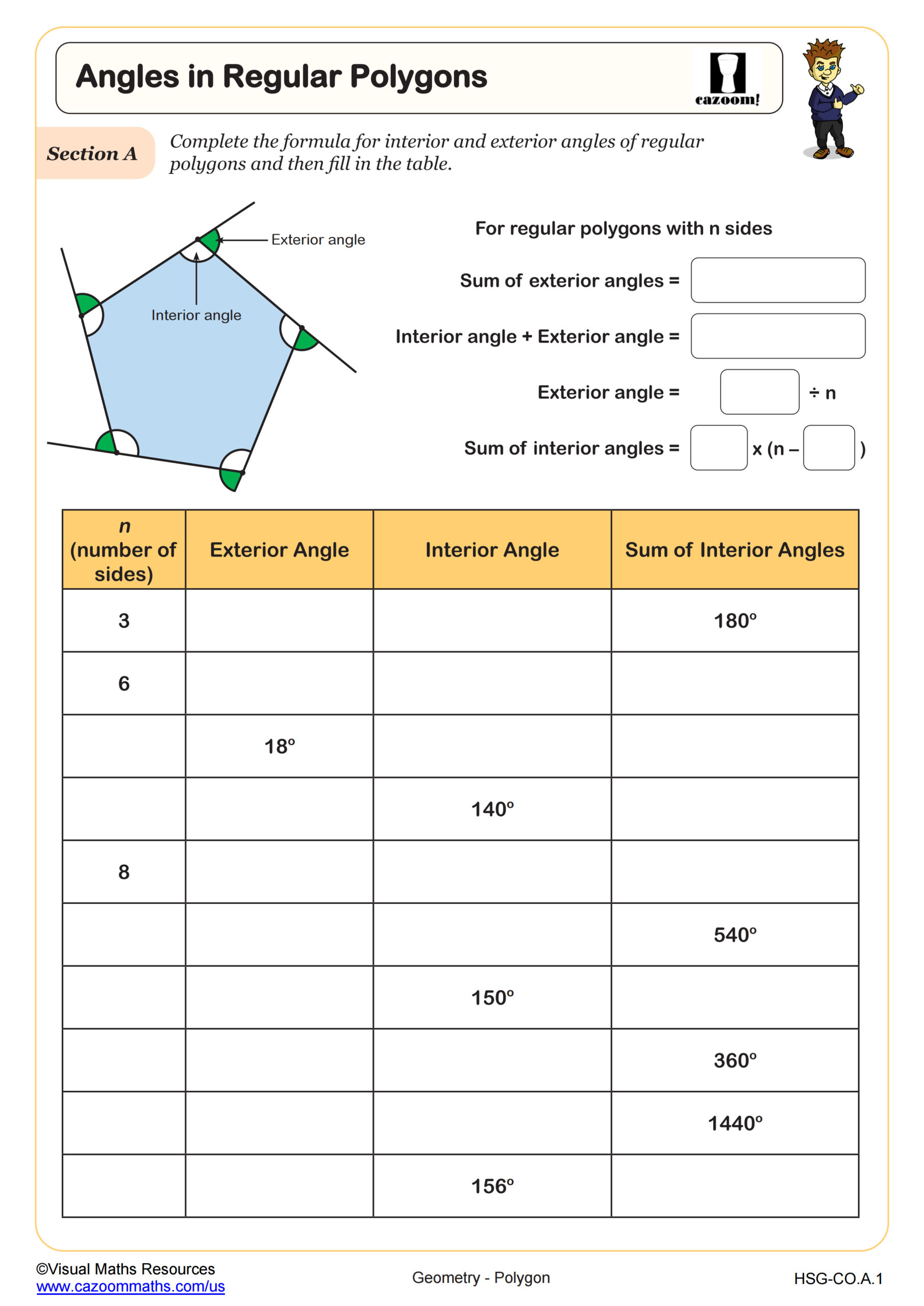
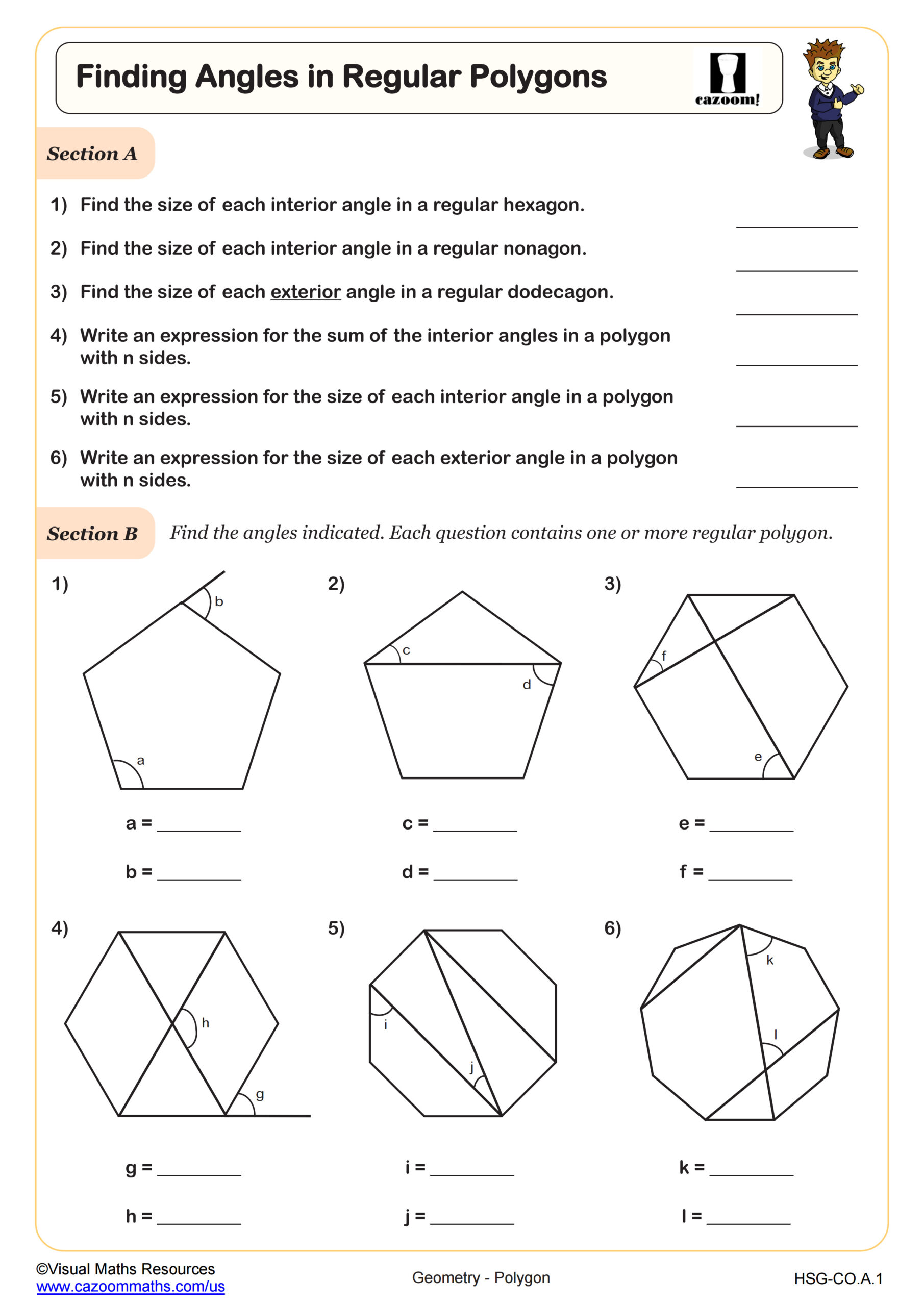
Students learn to calculate interior and exterior angles in both regular and irregular polygons, apply the formula (n-2)×180° for interior angle sums, and determine individual angle measures in regular polygons. The curriculum emphasizes understanding why these formulas work rather than just memorizing them, connecting polygon properties to prior knowledge about triangles and linear pairs.
A common misconception occurs when students try to apply regular polygon formulas to irregular shapes. Teachers frequently observe students assuming all quadrilaterals have 90-degree angles or that pentagons must be regular. Worksheets that mix regular and irregular examples help students distinguish when to divide the interior sum by the number of sides versus when they need additional information about individual angles.
How Are Polygons Tested on the SAT and State Assessments?
Standardized tests expect students to find missing angles in polygons embedded within larger diagrams, identify relationships between interior and exterior angles, and solve multi-step problems involving polygon properties. Questions often combine polygon angle relationships with other geometric concepts like parallel lines, requiring students to justify their reasoning rather than simply calculate.
Students lose points when they fail to show their work or misapply formulas under time pressure. A frequent error on assessments involves forgetting to subtract 2 before multiplying by 180 in the interior angle sum formula, or confusing the formula for one interior angle of a regular polygon with the sum formula. Practice with varied problem formats builds the flexibility needed for test success.
What Are Tessellations and Why Do They Matter?
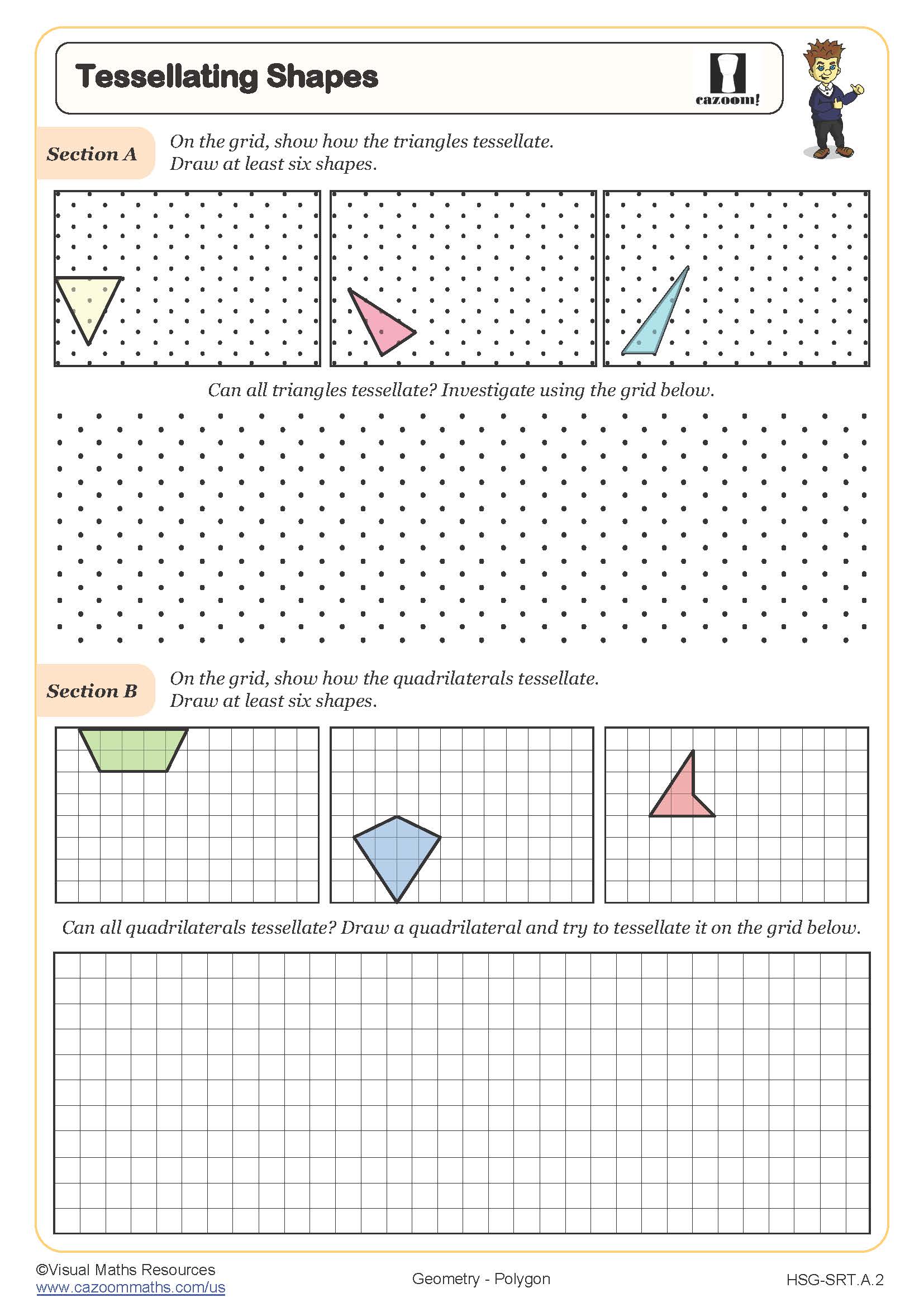
Tessellations are repeating patterns where polygons fit together without gaps or overlaps to cover a plane. Students explore which regular polygons tessellate on their own (only triangles, squares, and hexagons work because their interior angles divide evenly into 360°) and discover that combining different polygons creates semi-regular tessellations. This concept reinforces angle measurement while introducing symmetry and transformational geometry.
Tessellations appear throughout architecture, art, and engineering. Honeycomb structures use hexagonal tessellations for maximum strength with minimal material, while tile designers and urban planners apply tessellation principles to create functional and aesthetic patterns. Understanding why certain polygons tessellate helps students recognize the mathematical constraints behind design choices in STEM fields and prepares them for more advanced work in transformations and spatial reasoning.
How Can Teachers Use These Polygon Worksheets in Integrated Math 1?
The worksheets progress from regular polygon calculations to more complex irregular shapes and tessellation patterns, allowing teachers to scaffold instruction based on student readiness. Answer keys enable students to check their work independently during practice, while the variety of problem types helps teachers identify whether students truly understand angle relationships or are just applying formulas mechanically.
Many teachers use these worksheets for differentiated small-group work after introducing angle sum formulas, pairing stronger students with tessellation explorations while providing additional regular polygon practice for students still building foundational skills. The materials work well for test preparation since they mirror the format of state assessment questions. Teachers also assign specific worksheets for homework review before quizzes or use them as intervention resources when reteaching geometric reasoning concepts.