Integrated Math 1 Sequences Worksheets
What Do Students Learn About Sequences in Integrated Math 1?
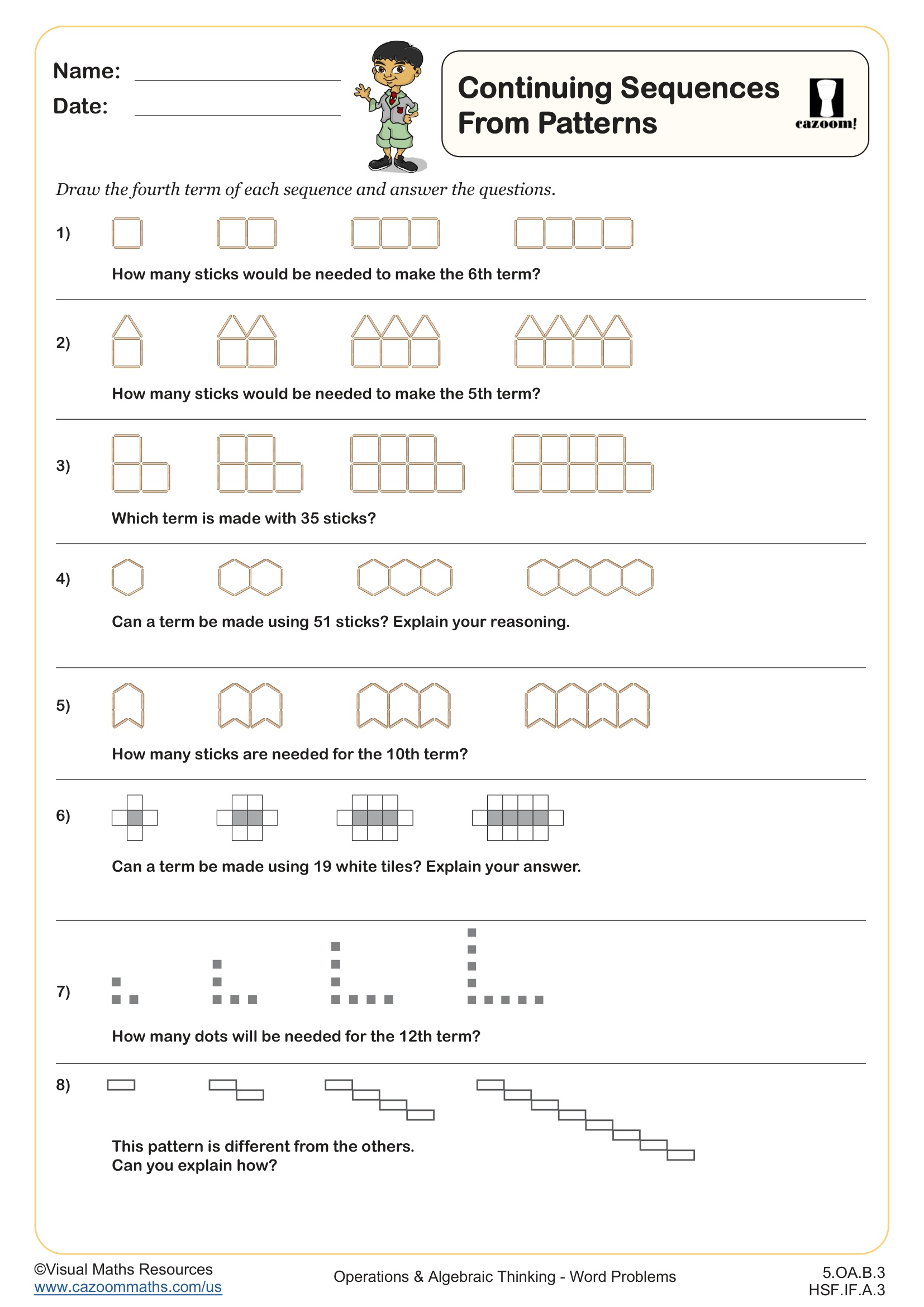
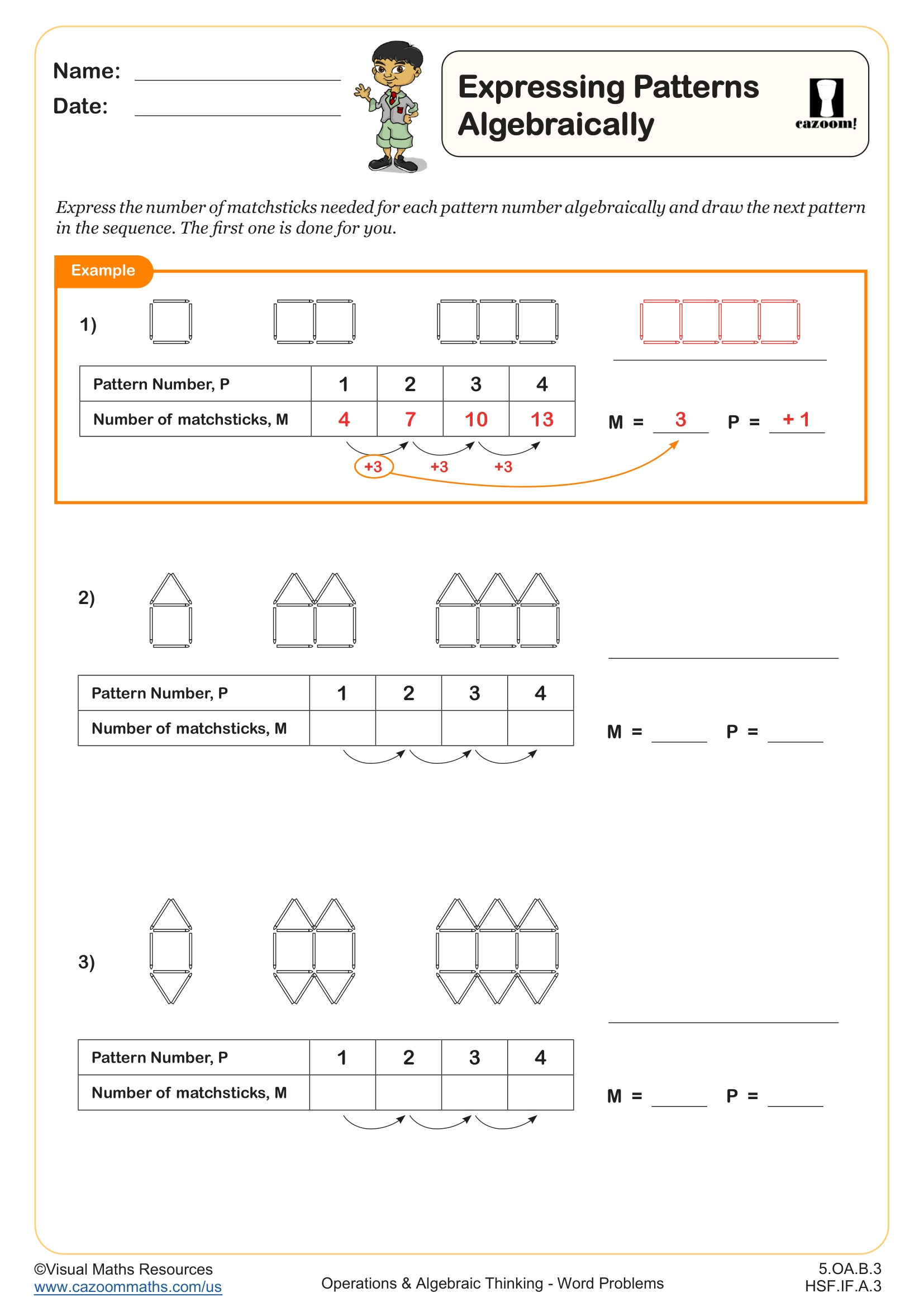
In Integrated Math 1, students learn to identify patterns in sequences, determine the rule governing each pattern, and express that rule using algebraic notation. They work with arithmetic sequences where a constant difference appears between consecutive terms, and they begin representing the nth term using variables and operations. This foundational work connects directly to functions and linear relationships introduced later in the course.
A common mistake students make involves confusing the term number with the term value. For example, in the sequence 5, 8, 11, 14, students might correctly identify that 14 is the fourth term but then write an incorrect expression because they substitute 14 instead of 4 into their formula. Teachers often use tables with separate columns for term position and term value to help students distinguish these concepts clearly.
How Do Sequences Appear on the SAT and State Assessments?
Standardized tests expect students to recognize patterns in sequences and apply algebraic rules to find missing terms or identify the nth term. Questions often present sequences in context, such as predicting the number of seats in the nth row of an auditorium or calculating the value of an investment after n years. Students must demonstrate fluency with both recursive thinking (what comes next) and explicit formulas (jumping directly to any term).
Students lose points when they fail to check their algebraic expressions against multiple terms in the sequence. Many students derive a formula that works for the first term but breaks down for subsequent terms because they miscounted the starting point or incorrectly identified the common difference. Test prep should emphasize verifying formulas by substituting at least three different term positions back into the original sequence.
What Is the Difference Between Recursive and Explicit Sequence Formulas?
A recursive formula describes how to get from one term to the next by stating the relationship between consecutive terms, while an explicit formula allows students to calculate any term directly using its position number. For the sequence 3, 7, 11, 15, a recursive formula might state that each term equals the previous term plus 4, whereas the explicit formula would be 4n - 1, where n represents the term position. Explicit formulas prove more efficient for finding terms far into the sequence.
This skill connects directly to computer science and programming, where recursive and iterative algorithms represent two fundamental approaches to problem-solving. Students pursuing STEM fields encounter these concepts again in calculus sequences and series, discrete mathematics, and when analyzing algorithm efficiency. Understanding both approaches builds mathematical flexibility that extends well beyond high school coursework.
How Can Teachers Use These Sequences Worksheets in Integrated Math 1?
The worksheets provide structured practice that progresses from visual pattern recognition through algebraic representation, allowing students to build conceptual understanding before formalizing their thinking. Teachers can assign the pattern-based worksheets first to activate prior knowledge from middle school, then move to expressing patterns algebraically once students demonstrate comfort with identifying rules. The answer keys enable students to self-check their work during independent practice or homework.
Many teachers use these worksheets as bell ringers to reinforce pattern recognition skills throughout the semester, not just during the sequences unit. The algebraic expression problems work well for station activities where students rotate through different types of sequences, or as intervention materials for students who need additional support before tackling linear functions. Paired work often helps struggling students articulate their thinking about patterns, while the answer keys allow partners to verify their reasoning immediately and adjust their approach.